算額（その1257）

算額（その1257）

百二十二 群馬県藤岡市東平井 諏訪神社 明治7年(1874)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円5個，正方形

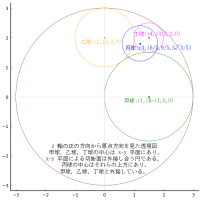
正方形の中に，中円，東円，西円，南円，北円の 5 個を容れる。東円，西円，南円，北円の直径が 7 寸，6 寸，3 寸，9 寸 のとき，正方形の一辺はいかほどか。

正方形の一辺の長さを a
中円の半径と中心座標を r1, (x1, y1)
東円の半径と中心座標を r2, (a - r2, a - r2)
西円の半径と中心座標を r3, (r3, r3)
南円の半径と中心座標を r4, (a - r4, r4)
北円の半径と中心座標を r5, (r5, a - r5)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, x1::positive, y1::positive,
     r2::positive, r3::positive, r4::positive, r5::positive;
eq1 = (a - r2 - x1)^2 + (a - r2 - y1)^2 - (r1 + r2)^2
eq2 = (x1 - r3)^2 + (y1 - r3)^2 - (r1 + r3)^2
eq3 = (a - r4 - x1)^2 + (y1 - r4)^2 - (r1 + r4)^2
eq4 = (x1 - r5)^2 + (a - r5 - y1)^2 - (r1 + r5)^2

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, r1, x1, y1) = u
   return [
-(r1 + r2)^2 + (a - r2 - x1)^2 + (a - r2 - y1)^2,  # eq1
-(r1 + r3)^2 + (-r3 + x1)^2 + (-r3 + y1)^2,  # eq2
-(r1 + r4)^2 + (-r4 + y1)^2 + (a - r4 - x1)^2,  # eq3
-(r1 + r5)^2 + (-r5 + x1)^2 + (a - r5 - y1)^2,  # eq4
   ]
end;

(r2, r3, r4, r5) = [7, 6, 3, 9] ./ 2
iniv = BigFloat[20, 8, 13, 8]

res = nls(H, ini=iniv)

   ([21.0, 7.625, 12.625, 7.5], true)

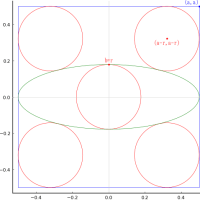
東円，西円，南円，北円の直径が 7 寸，6 寸，3 寸，9 寸 のとき，正方形の一辺は 21 寸である。

しかし，残念ながら，この算額の問題は欠陥がある。
正方形の一辺の長さは 21 寸になるが，中円が正方形からはみ出す。

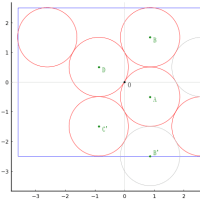
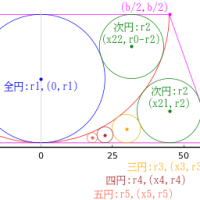
北円の直径を 8.9 寸程度にすると，正方形の一辺の長さは19.136 寸程度になり，「群馬の算額」の 140 ページにあるような図になる。

このような齟齬は，得られた解に基づいて正確な図を描いて検証するということがされていなかったことから生まれるのだろう。また，「群馬の算額」も含めて，第三者的立場でのチェックができていないということも根底にある。

その他すべてのパラメータは以下のとおりである。

  r2 = 3.5;  r3 = 3; , r4 = 1.5;  r5 = 4.45;  a = 19.1362;  r1 = 6.37033;  x1 = 11.6481;  y1 = 6.60738

function draw(r2, r3, r4, r5, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, r1, x1, y1) = res[1]
   @printf("東円，西円，南円，北円の直径が %g，%g，%g，%g のとき，正方形の一辺は %g である。\n",
       2r2, 2r3, 2r4, 2r5, a)
   @printf("r2 = %g;  r3 = %g; , r4 = %g;  r5 = %g;  a = %g;  r1 = %g;  x1 = %g;  y1 = %g\n",
       r2, r3, r4, r5, a, r1, x1, y1)
   plot([0, a, a, 0,  0], [0, 0, a, a, 0], color=:green, lw=0.5)
   circle(x1, y1, r1)
   circle(a - r2, a - r2, r2, :blue)
   circle(r3, r3, r3, :magenta)
   circle(a - r4, r4, r4, :orange)
   circle(r5, a - r5, r5, :brown)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       #hline!([0], color=:gray80, lw=0.5)
       #vline!([0], color=:gray80, lw=0.5)
       point(a, a, "(a,a)", :green, :right, :bottom, delta=delta/2)
       point(x1, y1, "中円:r1,(x1,y1)", :red, :center, delta=-delta/2)
       point(a - r2, a - r2, "東円:r2,(a-r2,a-r2)", :blue, :center, delta=-delta/2)
       point(r3, r3, "西円:r3,(r3,r3)", :magenta, :center, delta=-delta/2)
       point(a - r4, r4, "南円:r4,(a-r4,r4)", :black, :right,:bottom, delta=delta/2, deltax=5delta)
       point(r5, a - r5, "北円:r5,(r5,a-r5)", :brown, :center, delta=-delta/2)
   end
end;

draw(7/2, 6/2, 3/2, 9/2, true)