SymPy/Julia
https://www.math.csi.cuny.edu/~verzani/tmp/julia/symbolic.html
5. 数式の図示
数式は,Julia へ戻ることなく,直接プロットすることができる。
f(x) = sin(x^4) - cos(x^4) を [0,1] の範囲で描くには以下のようにする。
using Plots
gr(label="")
f(x) = sin(x^4) - cos(x^4)
plot(f(x), 0, 1)

plot の第一引数は関数でなくて,数式でよい。
g = sin(x^4) - cos(x^4)
plot(g, 0, 1)

f(x) も g も,どちらも Sym オブジェクトである。
println("f(x): $(f(x)), typeof(f(x)): $(typeof(f(x)))")
println("g: $g, typeof(g): $(typeof(g))")
f(x): sin(x^4) - cos(x^4), typeof(f(x)): Sym
g: sin(x^4) - cos(x^4), typeof(g): Sym
複数の数式は plot(), plot!() で図示する(一回の plot() 呼び出しだけで図示する方法はできなくなった)。
f(x) = sqrt(x)
fp = diff(f(x)) # fp は関数ではなく数式
c = 2
m = fp(x => c) # at c=2
println("c = $c, m = $m")
c = 2, m = sqrt(2)/4
plot(f(x), 1, 3)
plot!(f(c) + m * (x - c))

5.1. 課題
5.1.1. 問題 1.
x^4 - 3x^3 + 3x^2 - 3x +2 を [-1, 3] の範囲で描画せよ。実数解はいくつあるか。
g = x^4 - 3x^3 + 3x^2 - 3x + 2
plot(g, -1, 3)
savefig("fig4.png")
solve(g) |> println
real_roots(g) |> println
real_roots(g) |> length |> println
Sym[1, 2, -I, I]
Sym[1, 2]
2
6. 極限
limit() 関数は,数式の極限を求める。
limit() 関数の第 1 引数に数式を指定する。第 2 引数にどの変数について計算するか,第 3 引数はその変数をどこへ近づけていくかを指定する。
limit(sin(x)/x, x, 0) |> println
1
limit((1-cos(x))/x^2, x, 0) |> println
1/2
無限大は小文字の o を 2 個続けて表す。
limit(sin(x)/x, x, oo) |> println
0
関数の導関数は limit() 関数を使って数式計算できる(数値計算もできるが)。
@syms h
f(x) = x^10
limit((f(x + h) - f(x))/h, h, 0) |> println
10*x^9
diff() での結果とあっている。
diff(f(x)) |> println
10*x^9
同じ結果を与えるがもっと複雑な計算式を使う方法もある。
central_difference(f, x, h) = ( f(x + h) - f(x - h) ) / (2h)
a = limit(central_difference(f, x, h), h, 0) |> println
10*x^9
更にもっと複雑な計算式もある。
central_4th_difference(f, x, h) = (-f(x + 2h) + 8f(x + h) - 8f(x - h) + f(x - 2h))/(12h)
limit(central_4th_difference(f, x, h), h, 0) |> println
10*x^9
limit() はチェイン規則にしたがう。
func(x) = sin(x)
limit((f(func(x + h)) - f(func(x))) / h, h, 0) |> println # 10*sin(1)^9*cos(1)
10*sin(x)^9*cos(x)
6.1. 課題
6.1.1. 問題 1.
(3 - √(x + 5)) / (x - 4) の x を 4 に近づけていくときの極限を求めよ。
f(x) = (3 - sqrt(x + 5)) / (x - 4)
a = limit(f(x), x, 4)
println("a = $a, float(a) = $(float(a))")
a = -1/6, float(a) = -0.16666666666666666
6.1.2. 問題 2.
(x^(1/4) - 1) / (x^(1/3) - 1) の x を 1 に近づけていくときの極限を求めよ。
f(x) = (x^(1/4) - 1) / (x^(1/3) - 1)
limit(f(x), x, 1) |> float |> println
0.75
6.1.3. 問題 3.
記号変数 h を定義し,f(x) = sin(x) とする。
@syms h
f(x) = sin(x);
(f(x+h) - 2f(x) + f(x-h)) / h^2 の h を 0 に近づけていくときの極限は,何になるか。
gg = (f(x+h) - 2f(x) + f(x-h)) / h^2
limit(gg, h, 0) |> println
(diff(f(x), x), diff(f(x), x, 2), diff(f(x), x, 3)) |> println
-sin(x)
(cos(x), -sin(x), -cos(x))
この式は limit() 関数で 2 次の導関数を求めるための式である。
f(x) = 3x^3 + 2x^2 +3x + 4
limit(gg, h, 0) |> println
expand(diff(f(x), x, 2)) |> println
-sin(x)
18*x + 4
6.1.4. 問題 4.
記号変数 a を定義し,
(cos(a * x) - 1) / (cos(x) - 1) において x を 0 に近づけていくときの極限は,何になるか。
@syms a
limit((cos(a * x) - 1) / (cos(x) - 1), x, 0) |> println
a^2
6.1.5. 問題 5.
式 f(x) = 1/(x^(log(log(log(1/x)))-1)) の x を 0 に近づけていくときの極限を数値的に求めることができる。
f(x) = 1/(x^(log(log(log(1/x)))-1))
xs = 0.1 .^ (2:4:40)
fxs = [f(x) for x in xs]
[xs fxs]
10×2 Matrix{Float64}:
0.01 0.0702822
1.0e-6 0.619862
1.0e-10 27.0054
1.0e-14 2695.41
1.0e-18 4.65934e5
1.0e-22 1.20915e8
1.0e-26 4.32215e10
1.0e-30 2.00968e13
1.0e-34 1.16712e16
1.0e-38 8.21329e18
数式的に極限を求めると,結果は ∞ になり,数値的な場合に予測されたものに一致する(途中に float() を挟まない場合は,Inf を表す "oo" が表示される)。
limit(f(x), x, 0) |> float |> println
Inf
6.1.6. 問題 6.
式 f(x) = log(log(xexp(xexp(x)) + 1)) - exp(exp(log(log(x)) + 1/x)) で,x を ∞ に近づけていくときの極限を求めよ。
極限は 0 であるが,数値的に確認することはできない。
例えば f(10) をもとめてみよ。
f(x) = log(log(x*exp(x*exp(x)) + 1)) - exp(exp(log(log(x)) + 1/x))
f(x) |> println
-exp(exp(1/x)*log(x)) + log(log(x*exp(x*exp(x)) + 1))
f(10) |> println
Inf
確かに x = 10 の時点で Inf になってしまっている。
しかし,x として長精度実数を使うと実は結果は Inf ではないことがわかる。
f(big(10))
-0.4374481647059431342589507553638095674342208743587679099109922069614458809810611
喜びもつかの間,x が大きくなるとそのうち(いくら使用する精度を高くしても) Inf になってしまう(要するに想像を絶する大きな数値になるのだ)。
f(big(39))
Inf
limit() 関数を使えば,正しい答え 0 が導かれる。
limit(f(x), x, oo) |> println
0
7. 導関数
前述したように,limit() を使って導関数を求めることもできるが,SymPy には導関数を求めるための diff() 関数がある。
以下で,f(x) は 関数ではなく,数式 Sym である。
f(x) = exp(exp(x))
f (generic function with 1 method)
数式中に変数が 2 個以上ある場合は,どの変数について導関数を求めるかを指定する(デフォルトは x)。
diff(f(x)) |> println
diff(f(x), x) |> println
exp(x)*exp(exp(x))
exp(x)*exp(exp(x))
第三引数で何階導関数かを指定する(デフォルトでは 1)
diff(f(x), x, 2) |> println
(exp(x) + 1)*exp(x)*exp(exp(x))
x^x と,その導関数のグラフを描いてみる。
f(x) = x^x
plot(f(x), 1/10, 2, label="f(x)")
plot!(diff(f(x)), label="f'(x)")

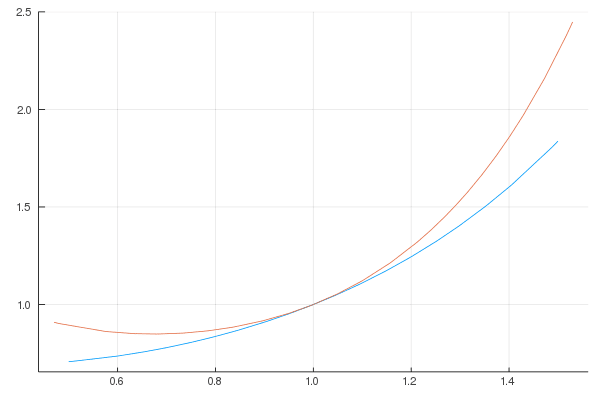
f(x) と c = 1 での切線のグラフを描く。
f(x) = x^x; c = 1
m = diff(f(x))
plot(f(x), .5, 1.5)
plot!(f(c) + m * (x - c))
7.1. 番外
diff() と solve() を組み合わせて,閉区間内の極値 f'(x) = 0 となる x を求めることができる。
3 辺の長さの和 L が一定の長方形の面積 A を最大にする問題を考えよう。
L = 2x + y
A = x * y
すなわち,A(x) = x * (L - 2x)
L を記号変数として,A'(x) = 0 となる x を求め,A(x) を求める。
@syms L, x, y
A = x*y
A = A(y => L - 2x)
out = solve(diff(A, x), x)[1]
out |> println # x
L/4
(L - 2x)(x => out) |> println # y
L/2
7.2. 課題
7.2.1. 問題 1.
tan(x)^(-1) の導関数を求めよ。
落とし穴(?)。tan(x)^(-1) は 1/tan(x) ではない。tan(x) の逆関数なので,atan(x) だ。
diff(atan(x)) |> println
1/(x^2 + 1)
微分は積分の逆なのだから,結果として提示されている 3 つの選択肢を integrate() してみればよい。atan(x) が解になる。
integrate(1/(x^2 + 1)) |> println
atan(x)
7.2.2. 問題 2.
f(x) = exp(-cos(x)) のとき,f'(3) を求めよ。
diff(exp(-cos(x)))(x => 3) |> println
diff(exp(-cos(x)))(x => 3) |> float |> println
exp(-cos(3))*sin(3)
0.3797841807457766324319619290395706689950768584935908050136628093384225996266999
7.2.3. 問題 3.
f(x) = 1/x^2 + x^3 の極値を求めよ。nsolve(diff(f(x)), 1) も試してみよ。
注: Julia では,? nsolve としても No documentation found. となるばかりだ。
Python の sympy で help(nsolve) でやっと,
Solve a nonlinear equation system numerically.
nsolve(f, [args,] x0, modules=['mpmath'])
'f' is a vector function of symbolic expressions representing the system.
args are the variables. If there is only one variable, this argument can
be omitted. 'x0' is a starting vector close to a solution.
@syms x::real
f(x) = 1/x^2 + x^3
solve(diff(f(x))) |> println
solve(diff(f(x))) |> float |> println
nsolve(diff(f(x)), 1) |> float |> println # 1 は初期値
Sym[2^(1/5)*3^(4/5)/3]
[0.9221079114817278]
0.9221079114817277656701705309291930146705850859540336029625316749125970624956978
7.2.4. 問題 4.
f(x) = tan(x) として, ニュートン法により 切線の方程式が f(c) + f'(c)(x-c) = 0 になるときの x を求めよ。
f(x) = tan(x)
@syms c
solve(f(c) + diff(f(c)) * (x - c), x) |> println
Sym[c - sin(2*c)/2]
c = pi/4 とすると何が得られるか?
solve(f(c) + diff(f(c)) * (x - c), x)[1](c => PI/4) |> float |> println
0.2853981633974483096156608458198757210492923498437764552437361480769541015715538
8. 積分(不定積分)
SymPy でも数式積分を行うことができるが,Mathematica に比べると劣る。
数値積分を行うのは integrate() である。
@syms x, a
f(x) = cos(x) - sin(x)
integrate(f(x), x) |> println
sin(x) + cos(x)
定数を含むこともできる。
integrate(1/cos(x + a), x) |> println
-log(tan(a/2 + x/2) - 1) + log(tan(a/2 + x/2) + 1)
その他の例
integrate(x^3 * (1-x)^4, x) |> println
x^8/8 - 4*x^7/7 + x^6 - 4*x^5/5 + x^4/4
integrate(x/(x^2+1), x) |> println
log(x^2 + 1)/2
9. 定積分
積分範囲を指定することで,定積分を計算することができる。
integrate(x^2, (x, 0, 1)) |> println
1/3
定積分の結果から,(分布関数の)中央値を計算することができる。
using SymPy
@vars x b real=true positive=true # 「b は正の実数」という条件を付けないと虚数解を含めて 4 個の解が求まる
f(x) = 4x^3
eq = integrate(f(x), (x, 0, b)) - 1/2 * integrate(f(x), (x, 0, 1));
println(eq)
solve(eq, b) |> float |> println
b^4 - 0.5
[0.8408964152537145]
9.1. 課題
9.1.1. 問題 1.
f(x) = 2 / (x * log(x)) の不定積分を求めよ。
integrate(2/(x * log(x))) |> println
2*log(log(x))
9.1.2. 問題 2.
f(x) = (2x + 5)(x^2 + 5x)^7 を [0, 1] で定積分せよ。
integrate((2x + 5) * (x^2 + 5x)^7, (x, 0, 1)) |> float |> println
209952.0
9.1.3. 問題 3.
f(x) = sqrt(4 - sqrt(x)) を [0,9] で定積分せよ。
integrate(sqrt(4 - sqrt(x)), (x, 0, 9)).evalf() |> println
12.5333333333333
integrate(sqrt(4 - sqrt(x)), (x, 0, 9)) |> float |> println ではエラーになる



























