算額(その75)
大阪府茨木市 井於神社 弘化3年(1846)
http://www.wasan.jp/osaka/iyo.html
鉤が 2 寸 7 分,股が 3 寸 6 分,弦が 4 寸 5 分の直角三角形の内部に正三角形が内接している。正三角形の一辺の長さを求めよ。

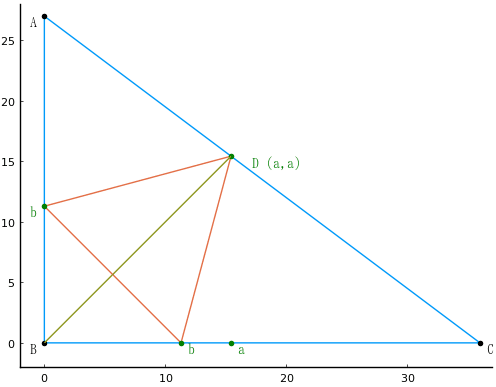
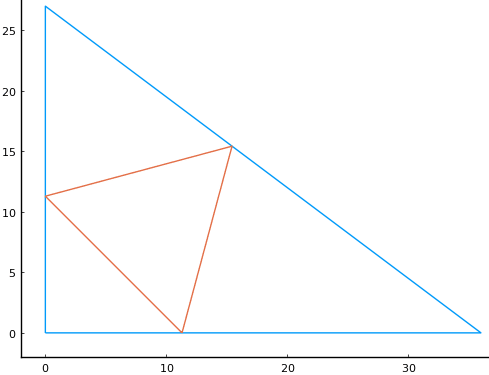
寸法を 10 倍し(「分」で表し)図のように記号を定め,方程式を解く。
算額の問題文に明確な記載はないが,∠DBC = 45° が仮定されているのだろうか(これ以外の仮定をする場合の解を後半に示す)。
using SymPy
@syms a::positive, b::positive, x::positive
a = 36*27//(36+27)
eq1 = (a-b)^2 + a^2 - x^2
eq2 = x/sqrt(Sym(2)) - b
solve([eq1, eq2])
1-element Vector{Dict{Any, Any}}:
Dict(b => sqrt(2)*(-108*sqrt(2)/7 + 108*sqrt(6)/7)/2, x => -108*sqrt(2)/7 + 108*sqrt(6)/7)
-108*sqrt(Sym(2))/7 + 108*sqrt(Sym(6))/7 |> factor |> println
-108*(-sqrt(6) + sqrt(2))/7
(√6 - √2)*108/7
15.972832497755562
正三角形の一辺の長さは (√6 - √2)*108/7 = 15.972832497755562 となる。もとの単位では 1寸5分9厘7毛...であるが,算額では1寸5分5厘8毛になっている。
using Plots
function point(x, y, string="", color=:green, position=:left, vertical=:top; fontsize=10, mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, fontsize, position, color, vertical))
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="")
a = 36*27/(36+27)
b = sqrt(2)*(-108*sqrt(2)/7 + 108*sqrt(6)/7)/2
x = 108*(sqrt(6) - sqrt(2))/7
println("x = $x")
plot([0, 36, 0, 0], [0, 0, 27, 0], xlims=(-2, 37), ylims=(-2, 28))
plot!([b, a, 0, b], [0, a, b, 0])
if more == true
point(0, 27, "A ", :black, :right)
point(0, 0, "B ", :black, :right)
point(36, 0, " C", :black)
point(a, a, " D (a,a)")
point(0, b, "b ", :green, :right)
point(a, 0, " a")
point(b, 0, " b")
plot!([0, a], [0, a])
end
end;
---
上述の解は,左下にできる三角形が二等辺三角形であると仮定したものである。この仮定の代わりに左下にできる三角形が外形の三角形と相似であると仮定した場合の解について考察してみる。
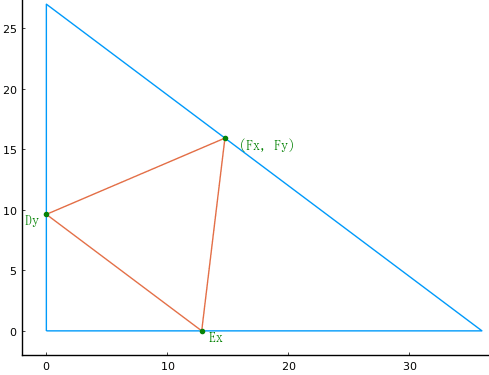
方程式は以下のようになる。正三角形の一辺を x として,5本の方程式を立てて解く。
using SymPy
@syms Dy::positive, Ex::positive, Fx::positive, Fy::positive, x::positive;
eq1 = Ex^2 + Dy^2 - x^2
eq2 = (Fx - Ex)^2 + Fy^2 - x^2
eq3 = Fx^2 + (Fy - Dy)^2 - x^2
eq4 = Dy - x*27//45
eq5 = 27Fx + 36Fy - 27*36; # 面積の制約
p = solve([eq1, eq2, eq3, eq4, eq5])
1-element Vector{Dict{Any, Any}}:
Dict(Ex => -6912/433 + 7200*sqrt(3)/433, Dy => -5184/433 + 5400*sqrt(3)/433, x => -8640/433 + 9000*sqrt(3)/433, Fx => 1008*sqrt(3)/433 + 4644/433, Fy => 8208/433 - 756*sqrt(3)/433)
p[1][x].evalf()
16.0472454229097
function draw2(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="")
p = Dict(Dy => -5184/433 + 5400*sqrt(3)/433, Ex => -6912/433 + 7200*sqrt(3)/433, Fx => 1008*sqrt(3)/433 + 4644/433, x => -8640/433 + 9000*sqrt(3)/433, Fy => 8208/433 - 756*sqrt(3)/433)
plot([0, 36, 0, 0], [0, 0, 27, 0], xlims=(-2, 37), ylims=(-2, 28))
plot!([0, p[Ex], p[Fx], 0], [p[Dy], 0, p[Fy], p[Dy]])
if more
println("x = $(p[x])\nDy = $(p[Dy])\nEx = $(p[Ex])\n(Fx, Fy) = $((p[Fx], p[Fy]))")
point(0, p[Dy], "Dy ", :green, :right)
point(p[Ex], 0, " Ex")
point(p[Fx], p[Fy], " (Fx, Fy)")
end
end
draw2(true)
x = 16.047245422909686
Dy = 9.628347253745813
Ex = 12.837796338327747
(Fx, Fy) = (14.757291487365883, 15.932031384475586)