算額（その1489）

算額（その1489）

五十 岩手県一関市西風 西風白山神社 弘化2年(1845)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，正方形
#Julia, #SymPy, #算額, #和算

正方形と大円が交わっており，隙間に小円 3 個を容れる。小円の直径が与えられたとき，大円の直径を求める術を述べよ。

追記：https://www.city.ichinoseki.iwate.jp/museum/wasan/h25/normal.html にあるように，図が曖昧なために難点が数々指摘されている。

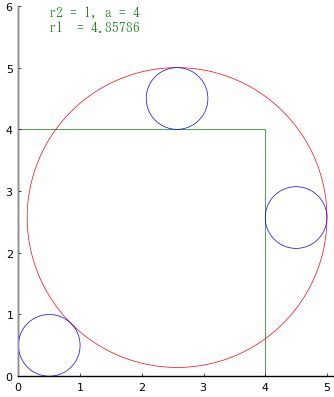
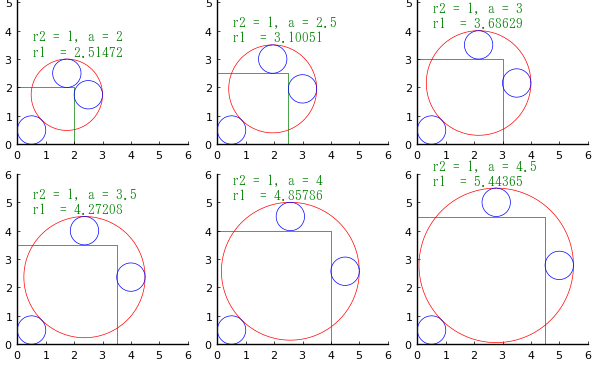
小円の直径が与えられただけでは，大円の直径は決まらない。小円の直径が同じでも，正方形の一辺の長さが違えば大円の直径も変わる。

制約条件としては正方形の大きさであろう。

大円と左下の小円の中心は正方形の対角線上にある。
また，右の小円の中心と大円の中心は水平線上に，上の小円の中心と大円の中心は垂直線上にある。
正方形の左下隅を原点とする。
正方形の一辺の長さを a
大円の半径と中心座標を r1, (x1, x1)
小円の半径と中心座標を r2, (r2, r2), (a + r2, x1), (x1, a + r2)
とおき，a, r2 を既知数，r1, x1 を未知数とする以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a, r1, x1, r2
eq1 = 2(x1 - r2)^2 - (r1 + r2)^2
eq2 = a - (x1 + r1 -2r2);

res = solve([eq1, eq2], (r1, x1))[1]  # 1 of 2

    (2*a + 3*r2 - sqrt(2)*(a + 2*r2), -a - r2 + sqrt(2)*(a + 2*r2))

術は「大円の直径 = (√8 + 4)*小円の直径」であるがなぜそうなるのか山村も教えてくれない。

function draw(a, r2, more=false)
    pyplot(size=(600, 400), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (r1, x1) = (2*a + 3*r2 - sqrt(2)*(a + 2*r2), -a - r2 + sqrt(2)*(a + 2*r2))
    p = plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
    circle(x1, x1, r1)
    circle(r2, r2, r2, :blue)
    circle(a + r2, x1, r2, :blue)
    circle(x1, a + r2, r2, :blue)
    point(r2, a + 4r2, @sprintf("r2 = %g, a = %g\nr1  = %g", 2r2, a, 2r1), mark=false)
    plot!(xlims=(0, 6), ylims=(0, 6))
    if more        
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end
    return p
end;

draw(4, 1/2, true)