算額（その1490）

算額（その1490）

五十五 岩手県花泉町老松 林観世音堂 文政7年(1824)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円14個，半円，円弧
#Julia, #SymPy, #算額, #和算

半円の中に円弧を描きできた隙間に，甲，乙，丙，丁，天，地，人の 14 個の円を容れる。丁円の直径が 77 寸のとき，人円の直径はいかほどか。

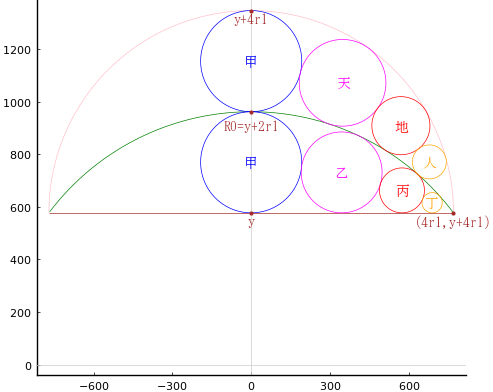
いつものように図は妥当ではないが，それはたいして問題ではない。

円弧の半径と中心座標を R0, (0, 0)
円弧の弦と y 軸の交点座標を (0, y)
甲円の半径と中心座標を r1, (0, y + r1), (0, y + 3r1)
半円の半径と中心座標を 4r1, (0, y + 2r1)
乙円の半径と中心座標を r2, (x2, y + r2)
丙円の半径と中心座標を r3, (x3, y + r3)
丁円の半径と中心座標を r4, (x4, y + r4)
天円の半径と中心座標を r5, (x5, y5)
地円の半径と中心座標を r6, (x6, y6)
人円の半径と中心座標を r7, (x7, y7)
とおき，以下の 16 元連立方程式を解く。（今までの最高次数だ）

include("julia-source.txt");

using SymPy

@syms R0, y, r1, r2, x2, r3, x3, r4, x4, r5, x5, y5, r6, x6, y6, r7, x7, y7
y = R0 - 2r1
eq1 = x2^2 + (y + r2)^2 - (R0 - r2)^2
eq2 = x3^2 + (y + r3)^2 - (R0 - r3)^2
eq3 = x4^2 + (y + r4)^2 - (R0 - r4)^2
eq4 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq5 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2
eq6 = (x4 - x3)^2 + (r3 - r4)^2 - (r3 + r4)^2
eq7 = (4r1)^2 + y^2 - R0^2
eq8 = x5^2 + (y5 - y)^2 - (4r1 - r5)^2
eq9 = x6^2 + (y6 - y)^2 - (4r1 - r6)^2
eq10 = x7^2 + (y7 - y)^2 - (4r1 - r7)^2
eq11 = x5^2 + y5^2 - (R0 + r5)^2
eq12 = x6^2 + y6^2 - (R0 + r6)^2
eq13 = x7^2 + y7^2 - (R0 + r7)^2
eq14 = x5^2 + (y + 3r1 - y5)^2 - (r1 + r5)^2
eq15 = (x6 - x5)^2 + (y5 - y6)^2 - (r5 + r6)^2
eq16 = (x7 - x6)^2 + (y6 - y7)^2 - (r6 + r7)^2;

using NLsolve

function nls(func, params...; ini = [0.0])
    if typeof(ini) <: Number
        r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
        v = r.zero[1]
    else
        r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
        v = r.zero
    end
    return Float64.(v), r.f_converged
end;

function H(u)
    (R0, r1, r2, x2, r3, x3, x4,  r5, x5, y5, r6, x6, y6, r7, x7, y7) = u
    return [
        x2^2 - (R0 - r2)^2 + (R0 - 2*r1 + r2)^2,  # eq1
        x3^2 - (R0 - r3)^2 + (R0 - 2*r1 + r3)^2,  # eq2
        x4^2 - (R0 - r4)^2 + (R0 - 2*r1 + r4)^2,  # eq3
        x2^2 + (r1 - r2)^2 - (r1 + r2)^2,  # eq4
        (r2 - r3)^2 - (r2 + r3)^2 + (-x2 + x3)^2,  # eq5
        (r3 - r4)^2 - (r3 + r4)^2 + (-x3 + x4)^2,  # eq6
        -R0^2 + 16*r1^2 + (R0 - 2*r1)^2,  # eq7
        x5^2 - (4*r1 - r5)^2 + (-R0 + 2*r1 + y5)^2,  # eq8
        x6^2 - (4*r1 - r6)^2 + (-R0 + 2*r1 + y6)^2,  # eq9
        x7^2 - (4*r1 - r7)^2 + (-R0 + 2*r1 + y7)^2,  # eq10
        x5^2 + y5^2 - (R0 + r5)^2,  # eq11
        x6^2 + y6^2 - (R0 + r6)^2,  # eq12
        x7^2 + y7^2 - (R0 + r7)^2,  # eq13
        x5^2 - (r1 + r5)^2 + (R0 + r1 - y5)^2,  # eq14
        -(r5 + r6)^2 + (-x5 + x6)^2 + (y5 - y6)^2,  # eq15
        -(r6 + r7)^2 + (-x6 + x7)^2 + (y6 - y7)^2,  # eq16
    ]
end;
r4 = 77/2
iniv = BigFloat[0.63267, 0.12628, 0.10193, 0.22742, 0.05565, 0.37825, 0.45332,
    0.10887, 0.22892, 0.32654, 0.07277, 0.7558, 0.2196, 0.04294, 0.44643, 0.12817].*1520
iniv = BigFloat[962, 192, 154, 344, 86, 574, 689, 165, 348, 1073, 111, 570, 909, 65, 678, 771]
res = nls(H, ini=iniv)

    ([962.5, 192.5, 154.0, 344.3544685349676, 85.55555555555556, 573.924114224946, 688.7089370699352, 165.0, 347.85054261852173, 1072.5, 110.58510638297872, 569.8828038643867, 909.2553191489362, 64.6544574982723, 678.1523018153765, 771.4633724948169], true)

丁円の半径が 77/2 寸のとき，人円の半径は 64.6544574982723 寸，直径は 129.3089149965446 寸である。

術は「人円の直径は，丁円の直径（77）を 135 倍して 77 で割ると，ほら，135 寸だよ」という，術とは名ばかりの，とんでもないものである。しかも誤差がある。

function draw(r4, more=false)
    pyplot(size=(600, 400), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (R0, r1, r2, x2, r3, x3, x4) = [0.63267, 0.12628, 0.10193, 0.22742, 0.05565, 0.37825, 0.45332]
    (R0, r1, r2, x2, r3, x3, x4,  r5, x5, y5, r6, x6, y6, r7, x7, y7) = res[1]
    y = R0 - 2r1
    x = sqrt(R0^2 - y^2)
    θ = atand(y, x)
    plot()
    segment(-x, y, x, y, :brown)
    circle(0, 0, R0, :green, beginangle=θ, endangle=180 - θ)
    circle(0, y + r1, r1, :blue)
    circle(x2, y + r2, r2, :magenta)
    circle(x3, y + r3, r3)
    circle(x4, y + r4, r4, :orange)
    println("2r7 = $(2r7)")
    circle(0, y, 4r1, :pink, beginangle=0, endangle=180)
    circle(0, R0 + r1, r1, :blue)
    circle(x5, y5, r5, :magenta)
    circle(x6, y6, r6)
    circle(x7, y7, r7, :orange)
    if more        
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, y + 3r1, "甲", :blue, :center, :vcenter, mark=false)
        point(x2, y + r2, "乙", :magenta, :center, :vcenter, mark=false)
        point(x3,y + r3, "丙", :red, :center, :vcenter, mark=false)
        point(x4, y + r4, "丁", :orange, :center, :vcenter, mark=false)
        point(0, y + r1, "甲", :blue, :center, :vcenter, mark=false)
        point(x5, y5, "天", :magenta, :center, :vcenter, mark=false)
        point(x6, y6, "地", :red, :center, :vcenter, mark=false)
        point(x7, y7, "人", :orange, :center, :vcenter, mark=false)
        point(0, y, "y", :brown, :center, delta=-delta)
        point(0, y + 2r1, "R0=y+2r1", :brown, :center, delta=-3delta)
        point(0, y + 4r1, "y+4r1", :brown, :center, delta=-delta)
        point(4r1, y, "(4r1,y+4r1)", :brown, :center, delta=-delta)
    end
end;

draw(77/2, true)