算額(その1575)
愛知県名古屋市中央区 大須観音(北野山真福寺寶生院) 天保8年(1837)
深川英俊,トニー・ロスマン:聖なる数学:算額,森北出版株式会社,2010年4月22日.
キーワード:円8個,外円
#Julia, #SymPy, #算額, #和算
外円の中に,大円 4 個,小円 3 個を容れる。外円と小円の直径が与えられたとき,大円の直径はいかほどか。
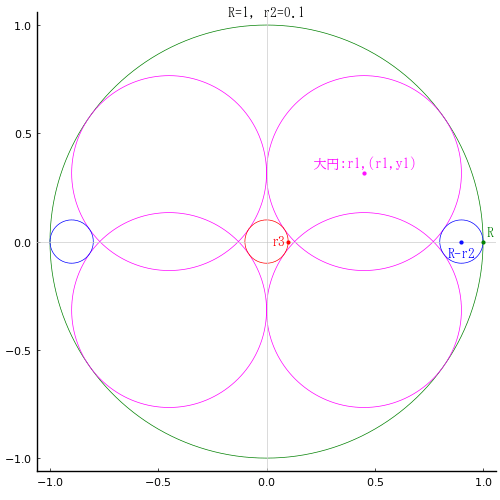
深川は,「中央の小円1と左右の小円2の直径の関係を示せ」という問題としている。
図を見ただけで直径は等しいとわかるが,ちゃんと式で示せということではある。
大円の中心の y 座標はどんな非負の値も取れるが,3個の小円の直径は同じであるということで,算額問題としては,「大円の直径を外円と小円の直径であらわせ」という問題にした。
include("julia-source.txt")
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r1::positive, y1::positive, r2::positive, r3::positive
eq1 = r1^2 + y1^2 - (R - r1)^2
eq2 = r1^2 + y1^2 - (r1 + r2)^2
res = solve([eq1, eq2], (r1, y1))[1]
(-(-R + r2)/2, sqrt(R)*sqrt(r2))
大円の直径は,外円の直径から小円の直径を差し引いたものの半分である。
外円の直径が同じでも,小円の直径により印象の異なる図が得られる。

function draw(R, r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, y1) = ((R - r2)/2, sqrt(R)*sqrt(r2))
r3 = r2
p = plot()
circle(0, 0, R, :green)
circle4(r1, y1, r1, :magenta)
circle2(R - r2, 0, r2, :blue)
circle(0, 0, r3)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, "R", :green, :left, :bottom, delta=delta/2, deltax=delta/2)
point(R - r2, 0, "R-r2", :blue, :center, delta=-delta)
point(r3, 0, "r3", :red, :right, :vcenter, deltax=-delta/2)
point(r1, y1, "大円:r1,(r1,y1)", :magenta, :center, :bottom, delta=delta/2)
pos = max(R, r2)
str = @sprintf(" R=%.3g, r2=%.3g", R, r2)
point(0, pos, str, :black, :center, :bottom, delta=delta, mark=false)
end
return p
end;
draw(1, 0.1, true)



























