算額(その1393)
四 武州川越町 八幡宮 寛政7年(1795)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
キーワード:円6個,共通接線,等脚台形
#Julia, #SymPy, #算額, #和算
共通接線2本を持つ 3 個の円が 2 セットある。甲円,乙円の直径が 81 寸,16 寸のとき,戊円の直径はいかほどか。
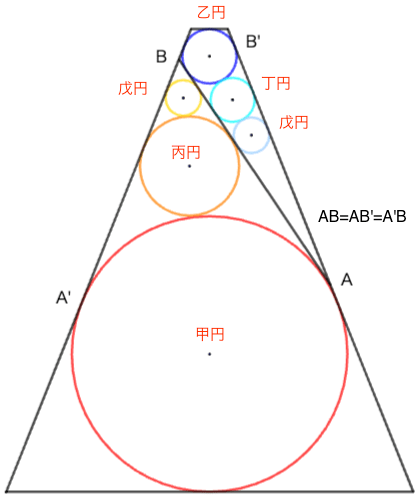
甲円,丙円,戊円と,乙円,丁円,戊円の 3 個の円が,共通接線 2 本で挟まれている。台形は必要な条件ではない。和算の心(その008)を 2 回適用し,連立方程式を解けばよい。
甲円,乙円,丙円,丁円,戊円の半径を r1, r2, r3, r4, r5 とする。
甲円,丙円,戊円のセットで,円の相似比を p
乙円,丁円,戊円のセットで,円の相似比を q
とする。
共通接線の交点から甲円との接点までの長さは 2r1*√p/(1 - p)
もう一組の共通接線の交点から乙円との接点までの長さは 2r2*√q/(1 - q)
一本の接線は共通なので,2 つの距離は等しい。
以上の関係式を eq0 としてまとめる。
using SymPy
@syms r1, r2, r5, p, q
p = sqrt(r5/r1)
q = sqrt(r5/r2)
eq0 = 2r1*√p/(1 - p) - 2r2*√q/(1 - q);
r1, r2 に実値を代入し,方程式を解き r5 を求める。
eq1 = eq0(r1 => 81//2, r2 => 16//2) |> simplify |> numerator
eq1 |> println
2^(1/4)*r5^(1/4)*(-211*sqrt(2)*sqrt(r5) + 684)
直径は r5 の 2 倍で,分数になる。
2solve(eq1, r5)[2] |> println # 2 of 2
467856/44521
帯分数は小学校時代以来使わないが,467856/44521 = 10 + 22646/44521 である。
divrem(467856,44521)
(10, 22646)