算額(その32)
岩手県一関市花泉町 大門神社・大門観世音菩薩 明治 33 年
http://www.wasan.jp/iwate/daimon5.html
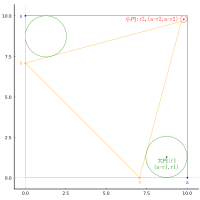
図のように,外円の中に 3 種類の円が入っている。そのうちの 3 つは直線に接している。
外円,小円,中円,大円の半径と中心座標を {1, (0, y3)}, {r1, (0, r1)}, {r2, (x2, r2)},{r3, (0, 2r1 + r3)} と置き,4 本の方程式を立てる。
しかし,これでは未知数 5 個に対して条件が一つ足りない。そこで,r1 を何らかの値に設定する。
r2, r3 も比較的きれいな分数式になるのは r1 = 7//64, 12//64, 15//64, 16//64 の 4 通りである。
算額的に最もきれいなのは次の解(r1 = 1/4)であろう。このとき,大円の径は小円の径の 2 倍になる。
r1 = 0.25, r2 = 0.375, r3 = 0.5
x2 = 0.6123724356957945, y3 = 0.5
using SymPy
@syms r1::positive, r2::positive, r3::positive, x2::positive, y3::positive;
r1 = 16 // 64
eq1 = x2^2 + (r2 - r1)^2 - (r1 + r2)^2
eq2 = x2^2 + (2r1 + r3 - r2)^2 - (r2 + r3)^2
eq3 = x2^2 + (y3 - r2)^2 - (1 - r2)^2
eq4 = 2r1 + 2r3 - y3 - 1;
res = solve([eq1, eq2, eq3, eq4], (r2, r3, x2, y3))
println("parameter = [$r1, $(res[1][1]), $(res[1][2]), $(res[1][3]), $(res[1][4])]")
parameter = [1//4, 3/8, 1/2, sqrt(6)/4, 1/2]
draw(parameter, false)
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top)
scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(parameter, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1, r2, r3, x2, y3 = parameter
println("r1 = $r1, r2 = $r2, r3 = $r3")
println("x2 = $x2, y3 = $y3")
plot()
circle(0, r1, r1, :green)
circle(x2, r2, r2, :blue)
circle(0, 2r1 + r3, r3, :magenta)
if more
point(0, 2r1+r3, "2r1+r3 ", :magenta, :right)
point(0, r1, "r1 ", :green, :right)
point(x2, r2, "(x2,r2)", :blue, :center)
point(0, y3, "y3 ", :black, :right)
vline!([0], color=:black, linewidth=0.25)
end
circle(0, y3, 1, :black)
hline!([0], color=:black, linewidth=0.25)
end;



























※コメント投稿者のブログIDはブログ作成者のみに通知されます