算額（その1520）

算額（その1520）

九　岩手県水沢市佐倉河 胆沢城八幡神社 弘化2年(1845)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図 03025
https://w.atwiki.jp/sangaku/pages/143.html

キーワード：直角三角形，正五角形，五芒星
#Julia, #SymPy, #算額, #和算

問：今有鈎股内如図設桔梗形(乃矩五角)其内面若干問得弦術如何

直訳：直角三角形の中に桔梗形を置き，その内部の五角形の一辺から弦を求める術を述べよ。

直角三角形の中に五芒星を描く。その頂点の 2 つは底辺（股）上に，もう 2 つは 斜辺（弦）上に，残りの 1 つが垂線（鈎）上にある。内部にできる正五角形の一辺の長さが与えられたとき，弦の長さを求める術を述べよ。

村山の図は本人自身も問が何を表しているのかわからなかったのであろう。図，問を自分勝手に解釈し，それに合うように術を作り変えてしまっている。本末転倒とはこのことだ。

「今有如図」はちゃんとした図を示している。この図があれば，解を求めるのは簡単である。

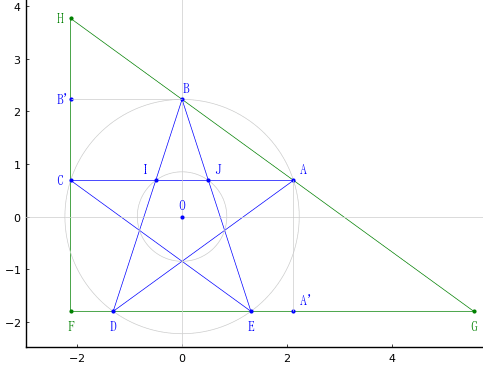
正五角形の一辺の長さを a とする。一般性を失わずに a = 1 と置くことができる。
正五角形が内接する円の半径を r，五芒星が内接する円の半径を R とおく。
五芒星の 5 個の頂点の x-y 座標を求める。
直角三角形の鈎，股はこれらの座標によって表すことができる。
鈎，股が得られれば，弦も求めることができる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r::positive, a::positive, outer::positive,
    s18, s36, s54, ax, ay, bx, by, cx, cy, dx, dy, ex, ey
a = 1  # IJ, 一般性を失わずに，内部の正五角形の一辺の長さを 1 と置くことができる
s18 = Sym(18)
s36 = Sym(36)  
s54 = Sym(54)
r = a/2cosd(s54)

R = r*sind(s54)/sind(s18)
# outer = 2R*sind(s36)  # 五芒星が内接する正五角形の一辺の長さ

(ax, ay) = (R*cosd(s18), R*sind(s18))
(bx, by) = (0, R)
(cx, cy) = (-ax, ay)
(ex, ey) = (R*sind(s36), -R*cosd(s36))
(dx, dy) = (-ex, ey)

股 = 2ax + (ax - dx)  # FG = CA + DA' = CA + A'G
鈎 = (ay - ey) + 2(by - cy)  # FH = AA' + 2B'C

弦 = sqrt(鈎^2 + 股^2);  # GH

弦は複雑な長い式で表されるが，簡約化すると (2√5 + 5) になる。

@syms d
apart(弦,d) |> println

    2*sqrt(5) + 5

弦は内部の正五角形の一辺の長さの (2√5 + 5) 倍である。

「術」の (√20 + 5) に一致した。

function draw(more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    a = 1  # 一般性を失わずに，内部の正五角形の一辺の長さを 1 と置くことができる
    (s18, s36, s54) = (18, 36, 54)
    r = a/2cosd(s54)
    R = r*sind(s54)/sind(s18)
    # outer = 2R*sind(s36)  # 五芒星が内接する正五角形の一辺の長さ
    (ax, ay) = (R*cosd(s18), R*sind(s18))
    (bx, by) = (0, R)
    (cx, cy) = (-ax, ay)
    (ex, ey) = (R*sind(s36), -R*cosd(s36))
    (dx, dy) = (-ex, ey)
    股 = 2ax + (ax - dx)
    鈎 = (ay - ey) + 2(by - cy)
    弦 = sqrt(鈎^2 + 股^2)
    (ix, iy) = float.(intersection(cx, cy, ax, ay, bx, by, dx, dy))
    @printf("R = %g;  鈎 = %g;  股 = %g;  弦 = %g\n", R, 鈎, 股, 弦)
    plot(cx .+ [0, 股, 0, 0], dy .+ [0, 0, 鈎, 0], color=:green, lw=0.5)
    plot!([ax, cx, ex, bx, dx, ax], [ay, cy, ey, by, dy, ay], color=:blue, lw=0.5)
    circle(0, 0, R, :gray80)
    circle(0, 0, r, :gray80)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(ax, ay, " A", :blue, :left, :bottom, delta=delta)
        point(ax, dy, " A'", :blue, :left, :bottom, delta=delta)
        segment(ax, ay, ax, dy, :gray80)
        point(bx, by, "B", :blue, :left, :bottom, delta=delta)
        point(cx, by, "B'", :blue, :right, :vcenter)
        segment(bx, by, cx, by, :gray80)
        point(cx, cy, "C ", :blue, :right, :vcenter)
        point(dx, dy, "D", :blue, :center, delta=-2delta)
        point(ex, ey, "E", :blue, :center, delta=-2delta)
        point(cx, dy, "F", :green, :center, delta=-2delta)
        point(cx + 股, dy, "G", :green, :center, delta=-2delta)
        point(cx, dy + 鈎, "H ", :green, :right, :vcenter)
        point(0, 0, "O", :blue, :center, :bottom, delta=delta)
        point(ix, iy, "I ", :blue, :right, :bottom, delta=delta)
        point(-ix, iy, " J", :blue, :left, :bottom, delta=delta)
        plot!(xlims=(cx - 10delta, cx + 股 + 5delta), ylims=(dy - 8delta, dy + 鈎 + 5delta))
    end
end;

draw(true)