算額(その1524)
二十七 一関市萩荘 赤萩観音寺 弘化4年(1847)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
今有如図 03034
https://w.atwiki.jp/sangaku/pages/307.html
キーワード:円3個,正三角形,正方形
#Julia, #SymPy, #算額, #和算
正方形の中に正三角形と大円 2 個,小円 1 個を容れる。正三角形の一辺の長さは正方形の一辺の長さに等しい。大円の直径が与えられたとき,小円の直径を求める術を述べよ。
山村の図は,(またしても)不適切である。その図に従って解を得ても「答」,「術」とは一致しない。
なお,直接の関係はないが,村山の図は「九十四 五葉神社」にある算額と同じである。しかし(当然ながら)それに対する「答」,「術」と本題の「答」,「術」は違う。
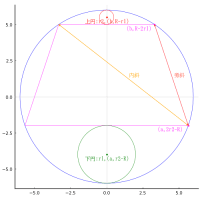
いつものごとく,「今有如図」の図は正しい。その図に従って得た解は「答」,「術」と一致する。

正方形,正三角形の一辺の長さを a
大円の半径と中心座標を r1, (a - r1, r1)
小円の半径と中心座標を r2, (a - r2, a - r2)
とおく。
正三角形の右上の頂点の座標は (a - r2 - r2/√2, a - r2 - r2/√2) となる。
以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive, r1::positive, r2::positive
s2 = √Sym(2)
b = a/√Sym(2)
eq1 = dist2(b, 0, a - r2 - r2/s2, a - r2 - r2/s2, a - r1, r1, r1)
eq2 = (a - r2 - r2/s2 - b)^2 + (a - r2 - r2/s2)^2 - a^2;
SymPy では一度に解くことができないが,eq2 は未知数が a だけなのですぐに解くことができる。
res = solve(eq2, r2)[1] # 1 of 2
res |> println
a*(-sqrt(3)*(2*sqrt(2) + 3) + (sqrt(2) + 3)*sqrt(2*sqrt(2) + 3))/(2*(2*sqrt(2) + 3)^(3/2))
@syms d
ans_r2 = apart(res, d) |> sympy.sqrtdenest |> simplify |> factor
ans_r2 |> println
-a*(-5 - sqrt(3) + sqrt(6) + 3*sqrt(2))/2
たとえば,一辺の長さが a = 10 のとき,小円の直径は 0.399203776664140 である。
ans_r2(a => 10).evalf() * 2 |> println
0.399203776664140
つぎに,eq1 の r2 に ans_r2 を 代入して,新たな方程式 eq11 とする。
eq11 = eq1(r2 => ans_r2) |> simplify
eq11 |> println
-sqrt(2)*a^2/2 - sqrt(6)*a^2/4 + 3*sqrt(3)*a^2/8 + 3*a^2/4 - 3*a*r1/2 - sqrt(3)*a*r1/2 + sqrt(6)*a*r1/4 + 3*sqrt(2)*a*r1/4 + r1^2/2
eq11 から r1 を求めると以下のようになる。
ans_r1 = solve(eq11, r1)[1] |> sympy.sqrtdenest |> simplify
ans_r1 |> println
a*(-3*sqrt(6) - 5*sqrt(2) + 4*sqrt(3) + 8)/4
たとえば,一辺の長さが a = 10 のとき,大円の直径は 2.54333095030250 である。
ans_r1(a => 10).evalf() * 2 |> println
2.54333095030250
問は,「大円径から小円径を得る術」であるから,r2/r1 を求めればよい。
apart(ans_r2/ans_r1, d) |> simplify |> println
-2*sqrt(3) - 2*sqrt(2) + sqrt(6) + 4
√6 - 2√3 - 2√2 + 4 で,SymPy ではそれ以上簡約化できないが,(2 - √2)*(2 - √3) であり,術と一致する。
なお,村山はここでも誤りを犯しており (2 - √2)*(3 - √3) としてしまっている。
小円の直径は,大円の直径の (2 - √2)*(2 - √3) = 0.15696100289923345 倍である。
(2 - √2)*(2 - √3)
0.15696100289923345
正方形の一辺の長さが 10 のとき,
大円の直径が 2.54333095030250 である。
そのとき,小円の直径は 2.54333095030250 * 0.15696100289923345 = 0.39920377666414086 となり,直接求めた小円の直径と一致する。
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
b = a/√2
r2 = -a*(-5 - sqrt(3) + sqrt(6) + 3*sqrt(2))/2
r1 = a*(-3*sqrt(6) - 5*sqrt(2) + 4*sqrt(3) + 8)/4
@printf("正方形の一辺の長さが %g のとき,大円の直径は %g,小円の直径は %g である。\n", a, 2r1, 2r2)
@printf("a = %g; b = %g; r1 = %g; r2 = %g\n", a, b, r1, r2)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
plot!([0, b, a - r2 - r2/√2, 0], [b, 0, a - r2 - r2/√2, b], color=:orange, lw=0.5)
circle(a - r1, r1, r1, :green)
circle(r1, a - r1, r1, :green)
circle(a - r2, a - r2, r2)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a - r1, r1, "大円:r1\n(a-r1,r1)", :green, :center, delta=-delta/2)
point(a - r2, a - r2, "小円:r2,(a-r2,a-r2) ", :red, :right, :vcenter)
point(a, 0, "a", :blue, :center, delta=-delta)
point(0, a, "a ", :blue, :right, :vcenter)
point(0, b, "b ", :orange, :right, :vcenter)
point(b, 0, "b", :orange, :center, delta=-delta)
plot!(xlims=(-5delta, a + 5delta), ylims=(-5delta, a + 5delta))
end
end;
draw(10, true)