スイッチを反転しても同じ数だけ点灯する?
締め切りが 2017/11/07 10:00 AM なので,その 1 分後に投稿されるように予約
設問
家庭に必ずある分電盤。その中にはブレーカーがあり、家庭内の電気スイッチやコンセントなどにつながっています。
ここでは、1つのブレーカーが2つのスイッチにつながっているものとします。
また、それぞれのスイッチに対して電球が1つずつ付いています。
スイッチをONにしても、そのスイッチにつながるブレーカーでONになっていないと電球は点灯しません。
もちろん、ブレーカーがONになっていても、スイッチがONになっていないと電球は点灯しません。
今、m 個のブレーカーがあり、n 個の電球が点灯しています。
ここで、すべてのスイッチを反転させたとき、点灯している電球の数が同じでした。
(あくまでもスイッチ部分の反転のみで、ブレーカーを触ることはありません。)
このようなブレーカー、スイッチの状態が何通りあるか求めます。
例えば、m = 2, n = 1 のとき、以下のような16通りがあります。
(色が付いている部分が点灯している部分)
同様に、m = 3, n = 2 のときは72通りがあります。
標準入力から m, n がスペース区切りで与えられたとき、上記のような状態が何通りあるか求め、
そのパターン数を標準出力に出力してください。
なお、m, n はともに20以下の正の整数とします。
【入出力サンプル】
標準入力
2 1
標準出力
16
=======================================================
m, n の小さい場合に対するプログラム(最後尾に記載)により,下図の配列 b を得る。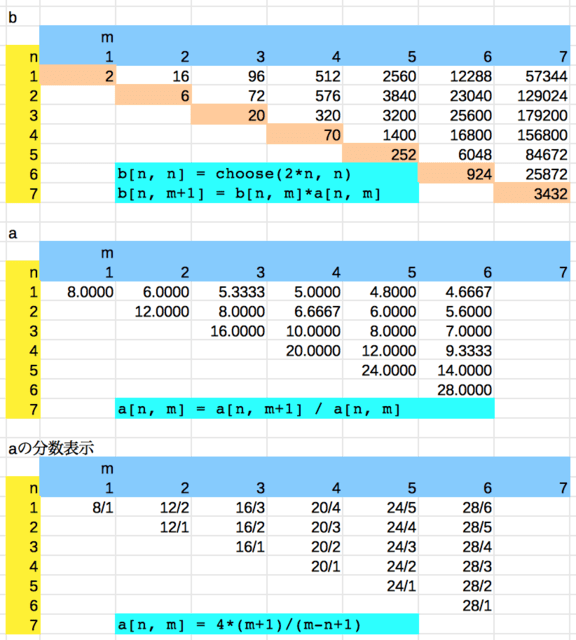
配列 b の対角成分 b[n, n] は choose(2*n, n)
n 行において b[n, m+1] = b[n, m] * a[n, m ]
配列 a は,分数表示すると,規則性があることがわかる。
a[n, m ] = 4*(m+1)/(m-n+1)
これをプログラム化する(面倒くさいので,m = n = 20 までの全てについて表を作る)。
f = function(M, N) {
options(scipen=100)
mx = 20
b = a = matrix(0, mx, mx)
for (m in 1:mx) {
for (n in m:1) {
a[n, m] = 4*(m+1)/(m-n+1)
}
}
for (n in 1:mx) {
b[n, n] = x = choose(2*n, n)
if (n < mx) {
for (m in n:(mx-1)) {
b[n, m+1] = b[n, m]*a[n, m]
}
}
}
cat(b[N, M])
}
f(2, 1) # 16
f(3, 2) # 72
f(10, 5) # 65028096
f(16, 15) # 9927521280
f(20, 20) # 137846528820
小規模な配列 b を求めるプログラム
f = function(m, n) {
library(e1071)
a = bincombinations(3*m)
count = 0
for (j in 1:nrow(a)) {
N1 = N2 = 0
for (i in 1:m) {
N1 = N1+sum(a[j, i]*a[j, m+2*i-1:0])
N2 = N2+sum(a[j, i]*(1-a[j, m+2*i-1:0]))
}
count = count + (N1 == N2 && N1 == n)
}
count
}


















