「ストレート・ラインズ」問題

「ストレート・ラインズ」問題

締め切りが 2017/11/23 10:00 AM なので，その 1 分後に投稿されるように予約

設問

2 以上の自然数 n に対し、n×n の格子状に並んだ点を考えます。
これらの点のうちちょうど 2 個の点を通る直線の数を F(n) と定義します。
 
例えば F(2)＝6 です。題意を満たす直線は以下の 6 通りです。
 

 
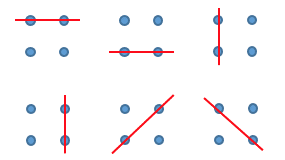
また、F(3)＝12 です。題意を満たす直線は以下の 12 通りです。
 

 
同様に、F(4)＝48, F(5)＝108, F(6)＝248, F(7)＝428, F(10)＝1900 となることが確かめられます。
 
標準入力から、自然数 n （2 ≦ n ≦ 40）が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。
 
===================================

問題文中にある数列情報だけで，オンライン整数列大辞典の A018809 であることがわかる。その説明書きが "Number of lines through exactly 2 points of an n X n grid of points." と，問題の趣旨そのものである。
ただ，記事中の (x, y) = 1 というのが何なのか，分からなかったが，関連する論文を読んで，「x, y の最大公約数が 1」ということが分かったのでプログラムを書き下ろす。

euclid = function(m, n) {
    repeat {
        temp = n%%m
        if (temp == 0) {
            return(m)
        }
        n = m
        m = temp
    }
}

g = function(n, k) {
    count = 0
    for (x in 0:n) {
        for (y in 0:n) {
            if (x != 0 && y != 0 && euclid(x, y) == k)
                count = count + (n - x) * (n - y)
        }
    }
    count
}

f = function(n) {
    if (n == 2) {
        cat(6)
    } else {
        cat(2 * g(n, 3) - 4 * g(n, 2) + 2 * g(n, 1))
    }
}

# f(scan(file("stdin", "r")))

#    n: 0  1  2   3   4    5    6    7    8     9    10
# f(n): 0, 0, 6, 12, 48, 108, 248, 428, 764, 1196, 1900
f(13) # 5244
f(27) # 98492
f(38) # 388212
f(40) # 475068