奥村先生が,「PIAACデータ解析」を書いている。(途中みたいだが)
https://oku.edu.mie-u.ac.jp/~okumura/stat/piaac.html
そのきっかけは
https://twitter.com/tmaita77/status/930020451899678720
https://twitter.com/kohske/status/930218156508946432
のようであるが,以下のようなプロットを作成すれば,実態が見えてくる。
データは31カ国の wh: 週あたり仕事時間(連続量) と ll: 新しいことを学ぶのが好き(5段階)
ただし,1カ国は wh が全て欠損値のため相関係数が計算できない(ので,除外する)
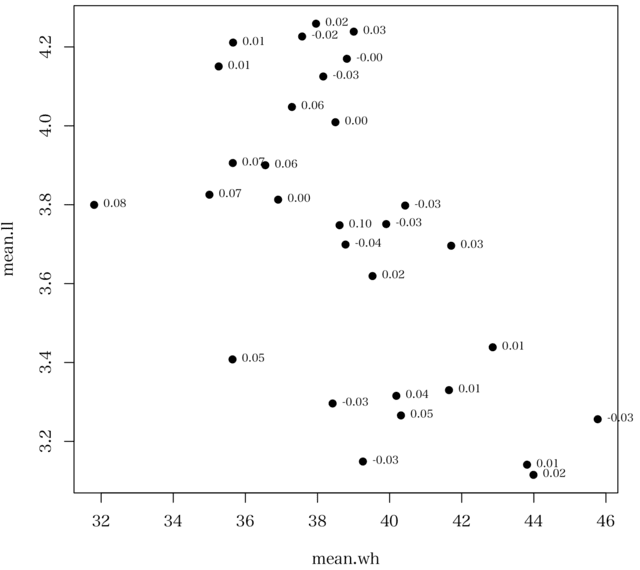
図には,黒丸で30カ国の wh, ll の平均値がプロットされている。
隣にある数値は,それぞれの国の対象者についての wh と ll のピアソンの積率相関係数である。各国での相関係数は小さなものである。無相関といってよい。
しかし,30カ国の wh と ll の平均値をデータとしたピアソンの積率相関係数はなんと -0.581 になる!!(図からも予想できるが)。なお,厳密にいえば(こんなところで厳密もへったくれもないが),30 個のデータ点はそれぞれの背景となったサンプルサイズによる重み付けが必要。
素データを国ごとにまとめた平均値間の相関係数は,実態を表さないのである。
もとの分析は,「新しいことを学ぶのが好き」の上位 2 カテゴリーに属するか否かの 2 値データにしたり,30〜40 歳代のフルタイムワーカーに限定したりしているが,大局的には大差ない。
また,「新しいことを学ぶのが好き」がカテゴリーデータなので,順位相関係数を求めても,またプロットの縦軸を mediann にしても,これまた大局的に大差ない。
library(data.table)
data = fread("all.dat")
cntryid = factor(data$CNTRYID)
wh = as.numeric(data$D_Q10) # 週あたり仕事時間
ll = as.numeric(data$I_Q04d) # 新しいことを学ぶのが好き
cor.wh.ll = sapply(data3, function(d) {
d2 = subset(d, complete.cases(d))
if (nrow(d2) == 0) NA else cor(d2$wh, d2$ll, use="complete.obs")
})
mean.wh = sapply(data3, function(d) mean(d$wh, na.rm=TRUE))
mean.ll = sapply(data3, function(d) mean(d$ll, na.rm=TRUE))
cor(mean.wh, mean.ll, method="spearman", use="complete.obs")
plot(mean.wh, mean.ll, pch=19)
text(mean.wh, mean.ll, sprintf("%.2f", cor.wh.ll), cex=0.7, pos=4, xpd=TRUE)
なお,all.dat は gawk, getdata.awk を使って
$ gawk -f getdata.awk *.csv > all.dat
で作成する(なんとなれば,それぞれの .csv ファイルの1行目が変数名なので)
getdata.awk ファイルの内容
NR == 1 { print }
FNR != 1 {print}



















