算額(その123)
長野県佐久市香坂 明泉寺千手観音堂 文化元年(1804)3月
http://www.wasan.jp/nagano/senju.html
五角形の中に大円と小円 2 個がある。上辺 18 寸,斜辺 25 寸のとき,大円の径はいかほどか。

算額(その117)に似ているが,台形ではなく五角形であるところがちょっと違う。
図が不鮮明であるが,[電子復刻 中村信弥著「改訂増補長野県の算額」] http://www.wasan.jp/zoho/nagano3.pdf に詳しいページ(74ページ)があった。
方程式を立てる都合上左右反転させる。
算額(その117)では,円の直径は AB * CD / (AB + CD) * 2 という公式があるが,本問では CD は 18 寸であるが,もう一つの長さが AB ではなく「AD の一部」が 25 寸とされている。「AD の一部」は,下図では DE である。DX は三角形の比例関係で求められるので,そのあとピタゴラスの定理で OX も求まり,件の公式が使える。
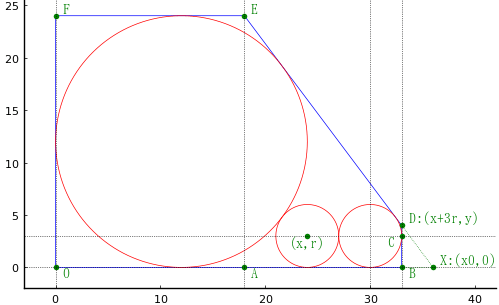
しかし,手で計算するのは面倒なので,以下のように方程式を立て,それを解く。
using SymPy
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))^2 # 二乗距離を返す!!
end;
@syms x0::positive, x::positive, y::positive, L::positive, r::positive, R::positive;
#@syms x0, x, y, L, r, R;
eq1 = (x + 3r - 18)^2 + (2R - y)^2 - 25^2 |> expand # ED の長さ
eq2 = (x - R)^2 + (R - r)^2 - (R + r)^2 |> expand # 大円と左の小円が外接する
eq3 = R*(x0-x-2r) - r*(x0-R) |> expand # R/r = (x0-R)/(x0-x-2r); R と r の比
eq4 = (x0 - 18)^2 + 4R^2 - L^2 |> expand # ⊿AXE EX を L とする
eq5 = 2R*(x0 - x - 3r) - y*(x0 - 18) |> expand # 2R/y = (x0-18)/(x0-x-3r); AE と BD の比
eq6 = distance(18, 2R, x0, 0, x+2r, r) - r^2; # 右の小円が EX に接する
例によって,複雑な方程式群は nlsolve() でなくては解けないようなので,以下のようにする。
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (x0, x, y, L, r, R))
println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
4*R^2 - 4*R*y + 9*r^2 + 6*r*x - 108*r + x^2 - 36*x + y^2 - 301,
R^2 - 4*R*r - 2*R*x + x^2,
-R*r - R*x + R*x0 - r*x0,
-L^2 + 4*R^2 + x0^2 - 36*x0 + 324,
-6*R*r - 2*R*x + 2*R*x0 - x0*y + 18*y,
-r^2 + (-2*R*(2*R*r - 2*r*x0 + 36*r - x*x0 + 18*x + x0^2 - 18*x0)/(4*R^2 + x0^2 - 36*x0 + 324) + r)^2 + (2*r + x - (4*R^2*x0 - 2*R*r*x0 + 36*R*r + 2*r*x0^2 - 72*r*x0 + 648*r + x*x0^2 - 36*x*x0 + 324*x)/(4*R^2 + x0^2 - 36*x0 + 324))^2,
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(x0, x, y, L, r, R) = u
return [
4*R^2 - 4*R*y + 9*r^2 + 6*r*x - 108*r + x^2 - 36*x + y^2 - 301,
R^2 - 4*R*r - 2*R*x + x^2,
-R*r - R*x + R*x0 - r*x0,
-L^2 + 4*R^2 + x0^2 - 36*x0 + 324,
-6*R*r - 2*R*x + 2*R*x0 - x0*y + 18*y,
-r^2 + (-2*R*(2*R*r - 2*r*x0 + 36*r - x*x0 + 18*x + x0^2 - 18*x0)/(4*R^2 + x0^2 - 36*x0 + 324) + r)^2 + (2*r + x - (-2*R*(4*R*r + 2*R*x - 2*R*x0 + r*x0 - 18*r) + (2*r + x)*(4*R^2 + x0^2 - 36*x0 + 324))/(4*R^2 + x0^2 - 36*x0 + 324))^2,
]
end;
iniv = [35.0, 22, 5, 31, 4, 13]
res = nls(H, ini=iniv)
println(res)
([36.000000000000014, 24.0, 4.000000000000003, 30.000000000000007, 3.000000000000002, 11.999999999999998], false)
大円の半径は 12 なので,もとの単位では直径が 24 寸 ということになる。
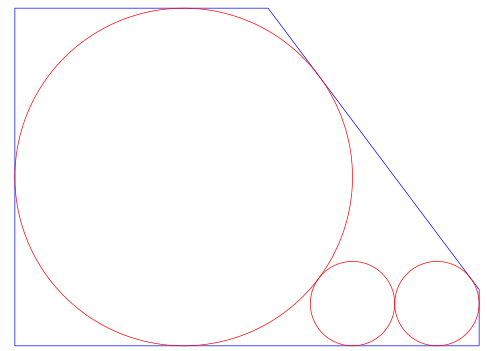
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
if fill
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
else
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x0, x, y, L, r, R) = res[1]
plot([0, x+3r, x+3r, 18, 0, 0], [0, 0, y, 2R, 2R, 0], color=:blue, lw=0.5)
circle(R, R, R)
circle(x, r, r)
circle(x+2r, r, r)
if more == true
point(0, 0, " O")
point(18, 0, " A")
point(x+3r, 0, " B")
point(x+3r, r, "C ", :green, :right)
point(x+3r, y, " D:(x+3r,y)", :green, :left, :bottom)
point(18, 2R, " E", :green, :left, :bottom)
point(0, 2R, " F", :green, :left, :bottom)
point(x0, 0, " X:(x0,0)", :green, :left, :bottom)
point(x, r, "(x,r)", :green, :bottom)
plot!([x+3r, x0, x+3r], [y, 0, 0], color=:green, lw=0.5, linestyle=:dot)
hline!([0, r], color=:black, lw=0.5, linestyle=:dot, xlims=(-3, 38), ylims=(-2, 26))
vline!([0, 18, 30, 33], color=:black, lw=0.5, linestyle=:dot)
else
plot!(showaxis=false)
end
end;


















