算額(その133)
岐阜県大垣市西外側町 大垣八幡神社 天保年間
http://www.wasan.jp/gifu/ogakihatiman.html
圭の中に甲円,乙円,丙円があり,甲円と乙円と別の丙円が外円の中にある。それぞれの円の径を求めよ。
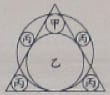
圭とは二等辺三角形である。最初正三角形だと勝手に解釈して解を求めようとしたが,求まらなかった。算額の問を読み返して,「圭」であることがわかった。
底辺の長さを 2 とする
圭の高さを y とする
図のように,記号を定め,方程式を解く
外円の中心座標と半径 (0, r0), r0
甲円の中心座標と半径 (0, 2r2+r1), r1
乙円の中心座標と半径 (0, r2), r2
右上の丙円の中心座標と半径 (x3, y3), r3
右下の丙円の中心座標と半径 (x4, r3), r3

using SymPy
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))^2 # 二乗距離を返す!!
end;
@syms y::positive, r0::positive, r1::positive, r2::positive, r3::positive, x3::positive, y3::positive, x4::positive;
eq1 = r2*(1 - x4) - r3 # r2 と r3 の比
eq2 = r1/r2 - (y - 2r2 - r1)/(y - r2)
eq3 = distance(1, 0, 0, y, x3, y3) - r3^2
eq4 = x3^2 + (y3 - r0)^2 - (r0 - r3)^2 # 外丙1
eq5 = x4^2 + (r0 - r3)^2 - (r0 + r3)^2 # 外丙2
eq6 = r1 + r2 - r0 # 外円の半径
eq7 = (y - r2)^2 - r2^2 * (y^2 + 1) # r2 と底辺の比
eq8 = r2*(sqrt(y^2 + 1) + 1) - y; # 面積
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (r0, r1, r3, x3, y3, x4, y, r2))
nlsolve() で解を求める。
println(simplify(eq1), ",")
println(simplify(eq2), ",")
println(simplify(eq3), ",")
println(simplify(eq4), ",")
println(simplify(eq5), ",")
println(simplify(eq6), ",")
println(simplify(eq7), ",")
println(simplify(eq8), ",")
-r2*x4 + r2 - r3,
(r1*y + 2*r2^2 - r2*y)/(r2*(-r2 + y)),
(-r3^2*y^2 - r3^2 + x3^2*y^2 - 2*x3*y^2 + 2*x3*y*y3 + y^2 - 2*y*y3 + y3^2)/(y^2 + 1),
x3^2 - (r0 - r3)^2 + (r0 - y3)^2,
-4*r0*r3 + x4^2,
-r0 + r1 + r2,
y*(-r2^2*y - 2*r2 + y),
r2*(sqrt(y^2 + 1) + 1) - y,
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r0, r1, r3, x3, y3, x4, y, r2) = u
return [
-r2*x4 + r2 - r3,
(r1*y + 2*r2^2 - r2*y)/(r2*(-r2 + y)),
(-r3^2*y^2 - r3^2 + x3^2*y^2 - 2*x3*y^2 + 2*x3*y*y3 + y^2 - 2*y*y3 + y3^2)/(y^2 + 1),
x3^2 - (r0 - r3)^2 + (r0 - y3)^2,
-4*r0*r3 + x4^2,
-r0 + r1 + r2,
y*(-r2^2*y - 2*r2 + y),
r2*(sqrt(y^2 + 1) + 1) - y,
]
end;
iniv = [0.8, 0.3, 0.16, 0.55, 1.11, 0.72, 1.81, 0.62]
res = nls(H, ini=iniv)
println(res)
([0.8304913036228202, 0.2235659941776492, 0.16186914316948992, 0.619774964637473,
1.0813589712444132, 0.7332964359033489, 1.921739300833543, 0.606925309445171], true)
外円の半径 = 0.830, 甲円の半径 = 0.224, 乙円の半径 = 0.607, 丙円の半径 = 0.162
圭の高さ = 1.922, x3 = 0.620, y3 = 1.081, x4 = 0.733

using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r0, r1, r3, x3, y3, x4, y, r2) = res[1]
@printf("外円の半径 = %.3f, 甲円の半径 = %.3f, 乙円の半径 = %.3f, 丙円の半径 = %.3f\n", r0, r1, r2, r3)
@printf("圭の高さ = %.3f, x3 = %.3f, y3 = %.3f, x4 = %.3f\n", y, x3, y3, x4)
plot([1, 0, -1, 1], [0, y, 0, 0], color=:black, lw=0.5)
circle(0, r2, r2)
circle(0, r0, r0, :green)
circle(0, 2r2+r1, r1, :blue)
circle(x4, r3, r3, :magenta)
circle(-x4, r3, r3, :magenta)
circle(x3, y3, r3, :magenta)
circle(-x3, y3, r3, :magenta)
if more == true
point(0, y, " y", :black, :left, :bottom)
point(0, r0, "外:(0,r0,r0)", :green)
point(0, 2r2+r1, "甲:(0,2r2+r1,r1)", :blue, :center, :top)
point(0, r2, "乙:(0,r2,r2)", :red)
point(x3, y3, "丙1:(x3,y3,r3)", :magenta, :center, :top)
point(x4, r3, "丙2:(x4,r3,r3)", :magenta, :center, :top)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;





















