算額(その127)
百二十四 群馬県桐生市天神町 天満宮 明治11年(1878)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
群馬県桐生市天神町 桐生天満宮 明治11年(1878)4月
http://www.wasan.jp/gunma/kiryutenmangu1.html
キーワード:円6個,外円
#Julia, #SymPy, #算額, #和算
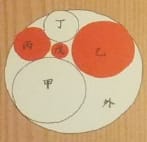
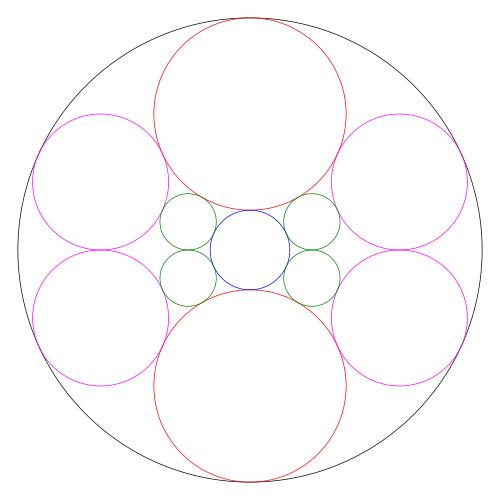
外円の中に 甲,乙,丙,丁,戊の円が入っている。乙円,丙円,戊円の径が 15寸,6寸,4寸であるとき,甲円,丁円,外円の径を求めよ。
復元奉納された算額は,もともとなのかもしれないが,正確な比率に基づくものではない。正解を書いているので,図の比率がおかしいのはすぐに分かるのではあるが。
http://www.wasan.jp/gunma/tenmangukaisetu.png
それにしても,方程式が 12 本というのは,今の所最多記録である。変数は 13 個であるが,どれか一つの円(丁円にした)の中心座標が 0 になるように回転するとすれば変数は 12 個になり無事方程式を解くことができる。
算額(その723)で解き直した。
https://blog.goo.ne.jp/r-de-r/e/4a0d1938c82c456123641ba6c54462d1
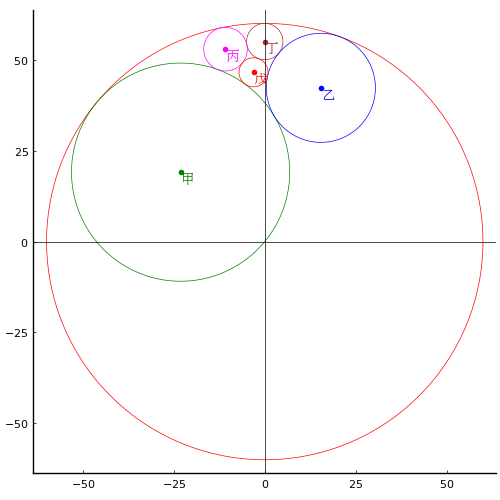
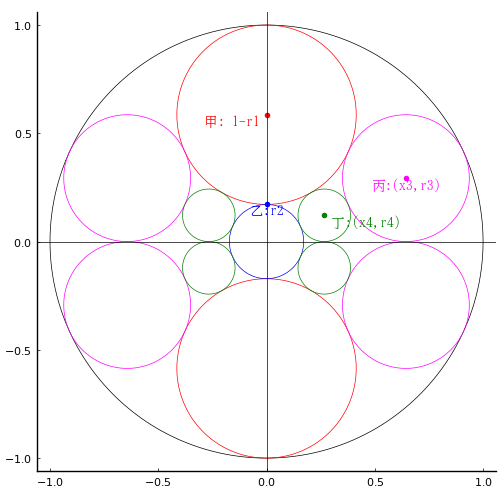
甲円の中心座標,半径 x1, y1, r1
丁円の中心座標,半径 0, y2, r2
乙円の中心座標 x3, y3
丙円の中心座標 x4, y4
戊円の中心座標 x5, y5
外円の半径 r0
using SymPy
@syms x1, y1, r1, x2, y2, r2, x3, y3, x4, y4, x5, y5, r0;
x2 = 0
eq1 = (x1 - x3)^2 + (y1 - y3)^2 - (r1 + 15)^2 # 甲乙
eq2 = (x1 - x4)^2 + (y1 - y4)^2 - (r1 +6)^2 # 甲丙
eq3 = (x1 - x5)^2 + (y1 - y5)^2 - (r1 + 4)^2 # 甲戊
eq4 = x1^2 + y1^2 - (r0 - r1)^2 # 甲外
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + 15)^2 # 乙丁
eq6 = (x3 - x5)^2 + (y3 - y5)^2 - (4 + 15)^2 # 乙戊
eq7 = x3^2 + y3^2 - (r0 - 15)^2 # 乙外
eq8 = (x4 - x5)^2 + (y4 - y5)^2 - (4 + 6)^2 # 丙戊
eq9 = x4^2 + y4^2 - (r0 - 6)^2 # 丙外
eq10 = (x2 - x4)^2 + (y2 - y4)^2 - (r2 + 6)^2 # 丁丙
eq11 = (x2 - x5)^2 + (y2 - y5)^2 - (r2 + 4)^2 # 丁戊
eq12 = x2^2 + y2^2 - (r0 - r2)^2; # 丁外
しかし例のごとく,nlsolve() でなくては解けない。また,初期値の設定に敏感なので手こずる。
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10, eq11, eq12])
println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
println(eq8, ",")
println(eq9, ",")
println(eq10, ",")
println(eq11, ",")
println(eq12, ",")
-(r1 + 15)^2 + (x1 - x3)^2 + (y1 - y3)^2,
-(r1 + 6)^2 + (x1 - x4)^2 + (y1 - y4)^2,
-(r1 + 4)^2 + (x1 - x5)^2 + (y1 - y5)^2,
x1^2 + y1^2 - (r0 - r1)^2,
x3^2 - (r2 + 15)^2 + (y2 - y3)^2,
(x3 - x5)^2 + (y3 - y5)^2 - 361,
x3^2 + y3^2 - (r0 - 15)^2,
(x4 - x5)^2 + (y4 - y5)^2 - 100,
x4^2 + y4^2 - (r0 - 6)^2,
x4^2 - (r2 + 6)^2 + (y2 - y4)^2,
x5^2 - (r2 + 4)^2 + (y2 - y5)^2,
y2^2 - (r0 - r2)^2,
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]))#, ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini)#, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(x1, y1, r1, y2, r2, x3, y3, x4, y4, x5, y5, r0) = u
return [
-(r1 + 15)^2 + (x1 - x3)^2 + (y1 - y3)^2,
-(r1 + 6)^2 + (x1 - x4)^2 + (y1 - y4)^2,
-(r1 + 4)^2 + (x1 - x5)^2 + (y1 - y5)^2,
x1^2 + y1^2 - (r0 - r1)^2,
x3^2 - (r2 + 15)^2 + (y2 - y3)^2,
(x3 - x5)^2 + (y3 - y5)^2 - 361,
x3^2 + y3^2 - (r0 - 15)^2,
(x4 - x5)^2 + (y4 - y5)^2 - 100,
x4^2 + y4^2 - (r0 - 6)^2,
x4^2 - (r2 + 6)^2 + (y2 - y4)^2,
x5^2 - (r2 + 4)^2 + (y2 - y5)^2,
y2^2 - (r0 - r2)^2,
]
end;
iniv = [-28.0, 26, 36, # x1, y1, r1 甲
67, 5, # y2, r2 丁
19, 51, # x3, y3 乙
-12, 64, # x4, y4 丙
-3, 57, # x5, y5 戊
63] .* (60/66)
res = nls(H, ini=iniv)
println(res)
([-23.141676475196107, 19.090909090909108, 30.00000000000001, 55.00000000000003, 5.000000000000002, 15.4277843167974, 42.2727272727273, -10.799449021758182, 52.909090909090935, -3.085556863359481, 46.54545454545457, 60.00000000000003], true)
外円の径 = 60.000, 甲円の径 = 30.000, 丁円の径 5.000 である。

using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
if fill
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
else
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x1, y1, r1, y2, r2, x3, y3, x4, y4, x5, y5, r0) = res[1]
@printf("外円の径 = %.3f, 甲円の径 = %.3f, 丁円の径 %.3f\n", r0, r1, r2)
x2 = 0
plot()
circle(0, 0, r0)
circle(x1, y1, r1, :green)
circle(x2, y2, r2, :brown)
circle(x3, y3, 15, :blue)
circle(x4, y4, 6, :magenta)
circle(x5, y5, 4)
if more == true
point(x1, y1, "甲", :green)
point(x2, y2, "丁", :brown)
point(x3, y3, "乙", :blue)
point(x4, y4, "丙", :magenta)
point(x5, y5, "戊", :red)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;