算額（その128）

算額（その128）

新潟県長岡市 蒼柴神社 亨和元年(1801)3月
http://www.wasan.jp/niigata/aoshi.html

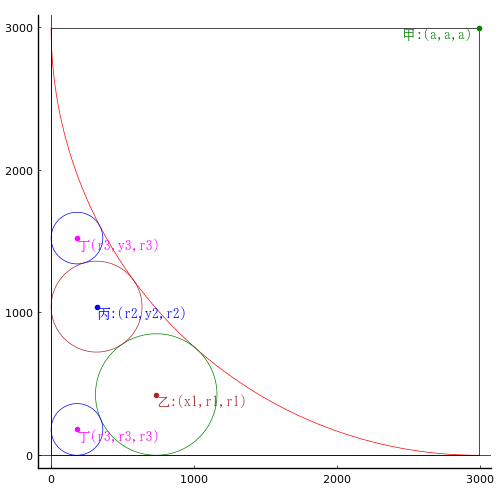
正方形内に甲円，乙円，丙円，丁円が入っている。甲円の径が 2993寸であるとき，丁円の径を求めよ。

以下のように記号を定め，方程式を立てて，解く。
甲円の中心座標，半径　a, a, a
乙円の中心座標，半径　x1, r1, r1
丙円の中心座標，半径　r2, y2, r2
丁円1の中心座標，半径　r3, y3, r3
丁円2の中心座標，半径　r3, r3, r3

using SymPy

@syms x1, r1, y2, r2, y3, r3;
@syms x1::positive, r1::positive, y2::positive, r2::positive, y3::positive, r3::positive;
a = 2993
eq1 = (a - x1)^2 + (a - r1)^2 - (a + r1)^2 # 甲乙
eq2 = (a - r2)^2 + (a - y2)^2 - (a + r2)^2 # 甲丙
eq3 = (a - r3)^2 + (a - y3)^2 - (a + r3)^2 # 甲丁
eq4 = (x1 - r2)^2 + (r1 - y2)^2 - (r1 + r2)^2 # 乙丙
eq5 = (x1 - r3)^2 + (r1 - r3)^2 - (r1 + r3)^2 # 乙丁
eq6 = (r2 - r3)^2 + (y2 - y3)^2 - (r2 + r3)^2; # 丙丁

res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (x1, r1, y2, r2, y3, r3))

   3-element Vector{NTuple{6, Sym}}:
    (2993*(-2705*sqrt(2)*sqrt(88*sqrt(2) + 145) - 3708*sqrt(88*sqrt(2) + 145) + 61516 + 43911*sqrt(2))/(14*(-97*sqrt(88*sqrt(2) + 145) - 64*sqrt(2)*sqrt(88*sqrt(2) + 145) + 1076*sqrt(2) + 1543)), 2993*(-53*sqrt(88*sqrt(2) + 145) + 6*sqrt(2)*sqrt(88*sqrt(2) + 145) + 154*sqrt(2) + 483)/(56*(-sqrt(88*sqrt(2) + 145) + 4*sqrt(2) + 7)), (-50881*sqrt(88*sqrt(2) + 145)/7 - 17958*sqrt(176*sqrt(2) + 290)/7 + 53874*sqrt(2) + 98769)/(-sqrt(88*sqrt(2) + 145) + 4*sqrt(2) + 7), -2993*sqrt(176*sqrt(2) + 290)/28 - 2993*sqrt(88*sqrt(2) + 145)/56 + 2993*sqrt(2)/4 + 20951/8, (-86797*sqrt(2) - 86797 + 14965*sqrt(88*sqrt(2) + 145)/7 + 50881*sqrt(176*sqrt(2) + 290)/7)/(-sqrt(88*sqrt(2) + 145) + 4*sqrt(2) + 7), -2993*sqrt(22*sqrt(2) + 145/4)/2 + 2993*sqrt(2) + 32923/4)
    (2993*(178476*sqrt(648*sqrt(2) + 1009) + 7918716 + 5633873*sqrt(2) + 129799*sqrt(2)*sqrt(648*sqrt(2) + 1009))/(46*(576*sqrt(2)*sqrt(648*sqrt(2) + 1009) + 25884*sqrt(2) + 37079 + 865*sqrt(648*sqrt(2) + 1009))), 2993*(70*sqrt(2)*sqrt(648*sqrt(2) + 1009) + 7958*sqrt(2) + 14835 + 501*sqrt(648*sqrt(2) + 1009))/(184*(12*sqrt(2) + 23 + sqrt(648*sqrt(2) + 1009))), (-29930*sqrt(1296*sqrt(2) + 2018)/23 + 77818*sqrt(2) + 218489 + 218489*sqrt(648*sqrt(2) + 1009)/23)/(12*sqrt(2) + 23 + sqrt(648*sqrt(2) + 1009)), -14965*sqrt(1296*sqrt(2) + 2018)/92 - 2993*sqrt(2)/2 + 50881/16 + 92783*sqrt(648*sqrt(2) + 1009)/368, (248419*sqrt(648*sqrt(2) + 1009)/23 + 607579 + 487859*sqrt(2) + 308279*sqrt(1296*sqrt(2) + 2018)/23)/(12*sqrt(2) + 23 + sqrt(648*sqrt(2) + 1009)), 8979*sqrt(2) + 80811/4 + 2993*sqrt(162*sqrt(2) + 1009/4)/2)
    (20951 + 17958*sqrt(2), 53874*sqrt(2) + 80811, 5986, 2993/4, 8979, 2993)

for i = 1:3
   println("\ni = $i")
   for j = 1:6
       println("$j $(res[i][j].evalf())")
   end
end

   i = 1
   1 736.025275189970
   2 425.487379588315
   3 1040.89692642305
   4 318.301571155078
   5 1520.94944962006
   6 181.000068733201

   i = 2
   1 14026.4495979657
   2 10168.4772828975
   3 7926.31625151136
   4 2032.87748391464
   5 31045.8991959313
   6 65733.8083275212

   i = 3
   1 46347.4471530960
   2 157000.341459288
   3 5986.00000000000
   4 748.250000000000
   5 8979.00000000000
   6 2993.00000000000

1 番目の解が妥当なものである。すなわち，元の単位では丁円の径は 181 寸である。

a*(11/4 + sqrt(2) - sqrt(22*sqrt(2) + 145/4)/2)

   181.00006873320254

丁円の半径は
-2993*sqrt(22*sqrt(2) + 145/4)/2 + 2993*sqrt(2) + 32923/4
である。甲円の半径を a = 2993 とすると
a*(sqrt(2) + 11/4 - sqrt(22*sqrt(2) + 145/4)/2)

答えとして，
「術に曰く，置く 11 箇，4 で歸し，これに斜率を加え，極と命名する」この部分が「11/4 + √2」である。整数は「箇」で数え，割り算は「歸」，√2 を「斜率」と呼ぶのか...
続いて，「自乗しこれから五分を引き，平方に開き，これを以て極より減ずる」この部分が「極 - sqrt(極^2 - 0.5)」
更に，「甲円の径を乗ずれば丁円の径が得られる」ということで「a * (極 - sqrt(極^2 - 0.5))」となる。
確かに，極^2 - 1/2 = 22*sqrt(2)/4 + 145/16 である

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
 θ = beginangle:0.1:endangle
 x = r.*cosd.(θ)
 y = r.*sind.(θ)
  if fill
      plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
  else
      plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
  end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x1, r1, y2, r2, y3, r3) = res[1]
   a = 2993
   @printf("乙円の径 = %.3f,  丙円の径 = %.3f,  丁円の径 %.3f\n", r1, r2, r3)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5)
   circle(a, a, a, beginangle=180, endangle=270)
   circle(x1, r1, r1, :green)
   circle(r2, y2, r2, :brown)
   circle(r3, y3, r3, :blue)
   circle(r3, r3, r3, :blue)
   if more == true
       point(a, a, "甲:(a,a,a) ", :green, :right)
       point(x1, r1, "乙:(x1,r1,r1)", :brown)
       point(r2, y2, "丙:(r2,y2,r2)", :blue)
       point(r3, y3, "丁(r3,y3,r3)", :magenta)
       point(r3, r3, "丁(r3,r3,r3)", :magenta)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

   乙円の径 = 425.487,  丙円の径 = 318.302,  丁円の径 181.000