算額（その1553）

算額（その1553）

四 岩手県花巻市南笹間 東光寺慶応2年(1866)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円，多角形，矢
#Julia, #SymPy, #算額, #和算

正 n 角形に矢を n 本引き，内部に相似な正 n 角形を作る。外側の正 n 角形の一辺の長さと，内側の正 n 角形に内接する甲円の直径が与えられたとき，周辺の合同な三角形に内接する乙円の直径を求めよ。

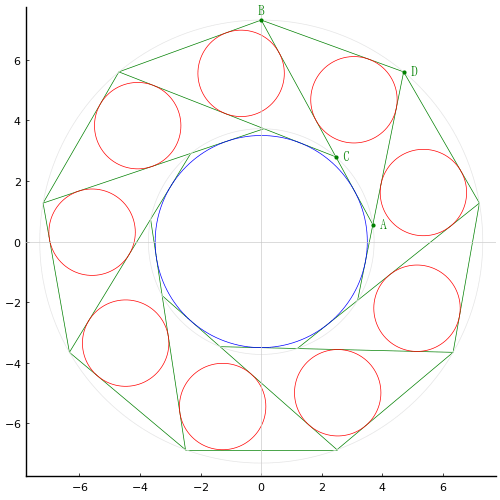
外側の正 n 角形が内接する円の半径を R
外側の正 n 角形の一辺の長さを a, 矢の長さを b + c; BD = a, DA = BC = b, AC = c
甲円の半径を r
とおき，以下の連立方程式を解く。

n, a, r が既知である。

include("julia-source.txt");
# # julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

三角形 ABD において，∠DAB について第二余弦定理を適用して b を求める。

@syms n, a, b, c, R, r, r2
c = 2r*tand(Sym(180)/n)
R = a/2sind(Sym(180)/n)
eq1 = a^2 - (b^2 + (b + c)^2 - 2b*(b + c)*cosd(Sym(360)/n))
ans_b = solve(eq1, b)[2]
ans_b |> println
ans_b(n => 7, a => 5, r => 3).evalf() |> println

    -r*tan(pi/n) + sqrt((4*r^2*sin(pi/n)^4 + (a^2 - 4*r^2*tan(pi/n)^2)*cos(pi/n)^2)*tan(pi/n)^2)/(2*sin(pi/n)^2)
    3.47458828453188

丙円の半径を求める。
丙円が内接する三角形の面積を表す二通りの方程式が等しいとする。

s = (a + b + (b + c))/2
eq2 = (a + b + (b + c))*r2/2 - sqrt(s*(s- a)*(s - b)*(s - (b + c)));
eq2 = eq2(b => ans_b) |> simplify
ans_r2 = solve(eq2[1], r2)[1]
ans_r2 |> println
ans_r2(n => 7, a => 5, r => 3).evalf() |> println

    sqrt(2)*sqrt(-(-a^2*sin(pi/n)^2 + a^2 - 4*r^2*sin(pi/n)^2)^2/(cos(4*pi/n) - 1))*sin(pi/n)^2/(a*sin(pi/n)^2 + sqrt((a^2 - 4*r^2*sin(pi/n)^2)*sin(pi/n)^2))
    1.16507932205657

丙円の半径は，sin(pi/n)，cos(4*pi/n) の関数として表すことができる。

t = sin(π/n)^2
u = a^2 - 4t*r^2
r2 = √2t*sqrt((u - a^2*t)^2/(1 - cos(4π/n)))/(a*t + sqrt(t*u))

以下は，図を描くためだけに必要なもの。

@syms θb, a, b, c
eq3 = a^2 + (b + c)^2 -2a*(b + c)*cosd(θb) - b^2
ans_θb = solve(eq3, θb)[2]
ans_θb |> println

    180*acos((a^2 + 2*b*c + c^2)/(2*a*(b + c)))/pi

@syms x3, y3, x01, y01, x02, y02
eq4 = dist(x01, y01, x02, y02, x3, y3) - r2^2
eq5 = dist(x01, y01, 0, R, x3, y3) - r2^2
res_x3 = solve(eq4, x3)[2];
eq5 = eq5(x3 => res_x3) |> simplify |> numerator
res_y3 = solve(eq5, y3)[2]
res_y3 |> println
res_x3 |> println

    (-a*r2*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2) + a*x01*y01 - a*x02*y01 + 2*r2*y01*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2)*sin(pi/n) + r2*(y01 - y02)*sqrt(a^2 - 4*a*y01*sin(pi/n) + 4*x01^2*sin(pi/n)^2 + 4*y01^2*sin(pi/n)^2) - 2*x01*y01*y02*sin(pi/n) + 2*x02*y01^2*sin(pi/n))/(a*x01 - a*x02 - 2*x01*y02*sin(pi/n) + 2*x02*y01*sin(pi/n))
    (r2*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2) - x01*y02 + x01*y3 + x02*y01 - x02*y3)/(y01 - y02)

function draw(n, a, r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    R = a/2sind(180/n)
    θ = 360/n
    θ2 = 90 .+ (0:θ:360)
    x = R.*cosd.(θ2)
    y = R.*sind.(θ2)
    b = -r*tan(pi/n) + sqrt((4*r^2*sin(pi/n)^4 + (a^2 - 4*r^2*tan(pi/n)^2)*cos(pi/n)^2)*tan(pi/n)^2)/(2*sin(pi/n)^2)
    c = 2r*tand(180/n)
    θb = 180*acos((a^2 + 2*b*c + c^2)/(2*a*(b + c)))/pi
    x01 = (b + c)*(cosd(θb + 180/n))
    y01 = R - (b + c)*sind(θb + 180/n)
    θ3 = atand(y01, x01)
    x2 = []
    y2 = []
    # r2 = sqrt(2)*sqrt(-(-a^2*sin(pi/n)^2 + a^2 - 4*r^2*sin(pi/n)^2)^2/(cos(4*pi/n) - 1))*sin(pi/n)^2/(a*sin(pi/n)^2 + sqrt((a^2 - 4*r^2*sin(pi/n)^2)*sin(pi/n)^2))
    t = sin(π/n)^2
    u = a^2 - 4t*r^2
    r2 = √2t*sqrt((u - a^2*t)^2/(1 - cos(4π/n)))/(a*t + sqrt(t*u))
    @printf("正%d角形の一辺の長さが %g，甲円の直径が %g のとき，乙円の直径は %g である。", n, a, 2r, 2r2)
    x02 = x[n]
    y02 = y[n]
    t = sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2)
    u = sin(pi/n)
    y3 = (-a*r2*t + a*x01*y01 - a*x02*y01 + 2*r2*y01*t*u + r2*(y01 - y02)*sqrt(a^2 - 4*a*y01*u + 4*x01^2*u^2 + 4*y01^2*u^2) - 2*x01*y01*y02*u + 2*x02*y01^2*u)/(a*x01 - a*x02 - 2*x01*y02*u + 2*x02*y01*u)
    x3 = (r2*t - x01*y02 + x01*y3 + x02*y01 - x02*y3)/(y01 - y02)
    l = c/2sind(180/n)
    for i = 1:n
        append!(x2, l*cosd(θ3))
        append!(y2, l*sind(θ3))
        θ3 += 360/n
    end
    plot()
    for i = 1:n
        segment(x[i], y[i], x[i + 1], y[i + 1], :green)
        segment(x[i], y[i], x2[i], y2[i], :green)      
    end
    circle(0, 0, R, :gray90)
    circle(0, 0, r, :blue)
    circle(0, 0, l, :gray90)
    rotate(x3, y3, r2, angle=360/n)
    if more        
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x01, y01, " A", :green, :left, :vcenter)
        point(x2[2], y2[2], " C", :green, :left, :vcenter)
        point(0, R, "B", :green, :center, :bottom, delta=delta/2)
        point(x[n], y[n], " D", :green, :left, :vcenter)
    end
end;

draw(9, 5, 3.5, true)