算額（その1244）

算額（その1244）

(9) 滋賀県マキノ町海津 天神社 明治8年(1875)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円3個，長方形，斜線2本

長方形の中に斜線を 2 本引き，大円 1 個，小円 2 個を容れる。長方形の長辺と短辺が 5 寸，4 寸，また，大円の直径が 2.2 寸のとき，小円の直径はいかほどか。

算額の図を見れば，長方形の長辺と短辺の比が 5:4 になっていないことが明白である。図面から測定すると，長方形の短辺を 4 寸とすれば，長辺は 5.788 寸，大円の直径は 2.73 寸である。上図はこの寸法で描いたものである。

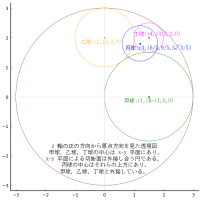
与えられた条件の寸法で解を求め，実際に図を書いてみると下図のようになる。小円は斜線と交わるし，小円は大円より大きい。

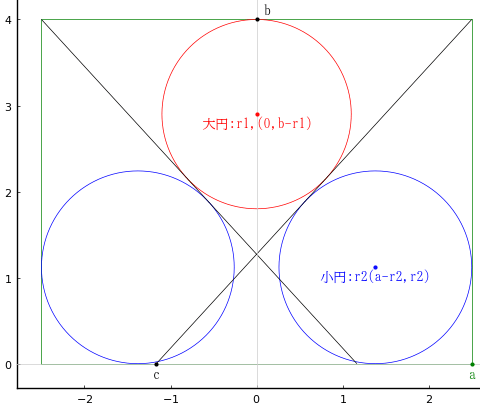
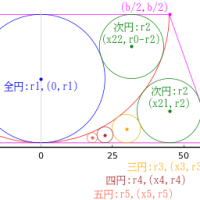
長方形の長辺と短辺を 2a, b
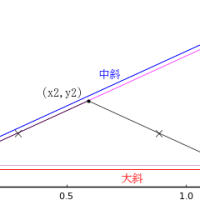
斜線と長方形の長辺の交点座標を (c, 0); c < 0
大円の半径と中心座標を r1, (0, b - r1)
小円の半径と中心座標を r2, (a - r2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::negative, r1::positive, r2::positive
eq1 = dist2(c, 0, a, b, 0, b - r1, r1)
eq2 = dist2(c, 0, a, b, a - r2, r2, r2)
res = solve([eq1, eq2], (r2, c))[1]

   ((a*b - b*r1)/(2*a), (-a^2*b + 2*a^2*r1 + b*r1^2)/(2*a*r1))

長方形の長辺と短辺が 5, 4，大円の直径が 2.2 のとき，小円の直径は 2.24 である。

その他のパラメータは以下のとおりである。

  a = 2.5;  b = 4;  r1 = 1.1;  r2 = 1.12;  c = -1.16545

function draw(a, b, r1, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, c) = ((a*b - b*r1)/(2*a), (-a^2*b + 2*a^2*r1 + b*r1^2)/(2*a*r1))
   @printf("長方形の長辺と短辺が %g, %g，大円の直径が %g のとき，小円の直径は %g である。\n", 2a, b, 2r1, 2r2)
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  c = %g\n", a, b, r1, r2, c)
   plot([a, a, -a, -a, a], [0, b, b, 0, 0], color=:green, lw=0.5)
   circle(0, b - r1, r1)
   circle2(a - r2, r2, r2, :blue)
   segment(c, 0, a, b)
   segment(-c, 0, -a, b)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, b - r1, "大円:r1,(0,b-r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "小円:r2(a-r2,r2)", :blue, :center, delta=-delta/2)
       point(a, 0, "a", :green, :center, delta=-delta)
       point(c, 0, "c", :black, :center, delta=-delta)
       point(0, b, " b", :black, :left, :bottom, delta=delta/2)
       plot!(xlims=(-a - 5delta, a + 5delta), ylims=(-5delta, b + 5delta))
   end
end;

draw(5/2, 4, 2.2/2, true)