算額（その1243）

算額（その1243）

(9) 滋賀県マキノ町海津 天神社 明治8年(1875)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：円4個，正三角形

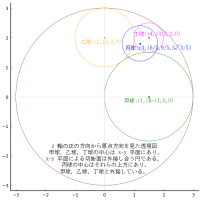
正三角形の頂点を中心とする天円，正三角形内に等円 3 個を容れる。等円の直径が 1 寸のとき，天円の直径，正三角形の一辺の長さはいかほどか。

「問」に「3 個の等円はそれぞれが，正三角形と 2 箇所で接する」と書かれているが，先に結論を書いておくが，この条件では図は描けない。

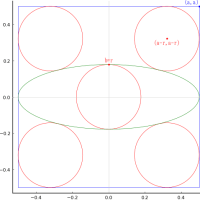
1.　「上の等円が正三角形の辺と 2 箇所で接する」とする場合

「答」では，「天円径三寸，三角面二寸八分〇六毛余」とあるので，「問」はこちらの場合を意図していたのであろう（正三角形の一辺の長さは不正確であるが）。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, a::positive
#@syms r1, r2, a
eq1 = r2^2 + (√Sym(3)a - r2)^2 - (r1 + r2)^2
eq2 = dist2(a, 0, 0, √Sym(3)a, 0, √Sym(3)a - r1 + r2, r2)
res = solve([eq1, eq2], (r1, a))[1]

   (7*r2*(-6*sqrt(15)/7 - 6/7)/12 - r2/2 + 49*r2*(-6*sqrt(15)/7 - 6/7)^2/144, -7*sqrt(3)*r2*(-6*sqrt(15)/7 - 6/7)/18)

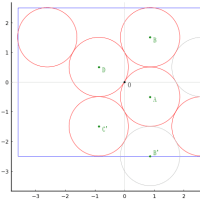
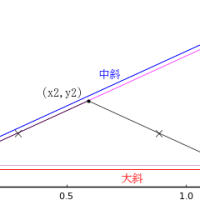
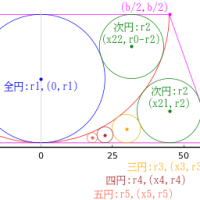
2.　「下の等円が正三角形の辺と 2 箇所で接する」とする場合

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, a::positive
#@syms r1, r2, a
eq1 = r2^2 + (√Sym(3)a - r2)^2 - (r1 + r2)^2
eq3 = dist2(a, 0, 0, √Sym(3)a, r2, r2, r2)
res = solve([eq1, eq3], (r1, a))[3]

   (sqrt(2)*sqrt(r2)*sqrt(r2 + sqrt(3)*r2 + r2*(sqrt(3) + 3)) - r2, 2*sqrt(3)*r2/3 + r2*(sqrt(3) + 3)/3)

3.　なぜこのような齟齬が生じるのか

算額を解く「和算」では，図形全体としての整合性の確認がおろそかだったのではないか。この「問」では，天円の直径と正三角形の一辺の 2 パラメータを求めよとしているが，多くの算額ではただ 1 つのパラメータを求めよとするものが普通である。この算額でも，実際に図を描いてみると，「3 個の等円はそれぞれが，正三角形と 2 箇所で接する」という条件を満たすことができないことはすぐに分かることである。もう一つの原因は，精密な図を描くことが難しかったので，「ちょっと接していないようだが，誤差範囲だよね」ということもあったのだろう。
「〇〇の算額」という書籍が何冊か発行されているが，著者がすべての問題を解いて，「問」，「答」，「術」の妥当性を確かめたとは思えない（不適切な解がそのまま載っている）ことが稀にあるのが残念である。

function draw(r2, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, a) = (7*r2*(-6*sqrt(15)/7 - 6/7)/12 - r2/2 + 49*r2*(-6*sqrt(15)/7 - 6/7)^2/144, -7*sqrt(3)*r2*(-6*sqrt(15)/7 - 6/7)/18)
   (r1, a) = (sqrt(2)*sqrt(r2)*sqrt(r2 + sqrt(3)*r2 + r2*(sqrt(3) + 3)) - r2, 2*sqrt(3)*r2/3 + r2*(sqrt(3) + 3)/3)
   string = @sprintf("上の等円が斜辺に接するように立式したとき\n等円の直径 = %g\n天円の直径 = %g\n正三角形の一辺の長さ = %g", 2r2, r1, 2a)
   @printf("等円の直径が %g のとき，天円の直径は %g，正三角形の一辺の長さは %g である。\n", 2r2, r1, 2a)
   @printf("r2 = %g;  r1 = %g;  a = %g\n", r2, r1, a)
   plot([a, 0, -a, a], [0, √3a, 0, 0], color=:green, lw=0.5)
   circle(0, √3a, r1)
   circle(0, √3a - r1 + r2, r2, :blue)
   circle2(r2, r2, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, √3a + 15delta, string, :black, :left, deltax=-22delta, mark=false)
       point(0, √3a, "天円:r1,(0,√3a)", :red, :center, :bottom, delta=delta)
       point(r2, r2, "等円:r2,(r2,r2)", :blue, :center, :bottom, delta=delta)
       point(0, √3a - r1 + r2, "等円:r2\n(0,√3a-r1+r2)", :blue, :center, :bottom, delta=delta)
   end
end;

draw(1/2, true)