異なる整数で作る逆三角形

異なる整数で作る逆三角形

締め切りが 2017/05/23 10:00 AM なので，その 1 分後に投稿されるように予約

設問

n 個の自然数を1段目に並べます。
2段目は n-1 個の自然数を、3段目は n-2 個の自然数を、…というように、図のように逆三角形の形に並べます。
このとき、2段目以降の自然数はそれぞれ、その自然数の左上と右上の数の和とします。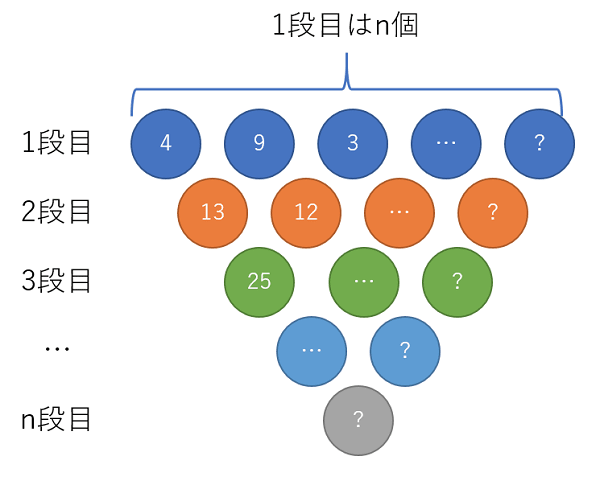

n 段目までに登場するすべての数が重複しないように1段目の数を選んだ時、n 段目の数が最小になるものを求めます。
ただし、いずれの数も正の整数とします。
例えば、n = 3 のとき、以下の左のようにすると3が重複しています。
そこで、右のように配置すると重複はなく、3段目が最小である「8」となります。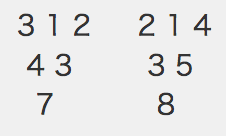

標準入力から n が与えられたとき、標準出力に n 段目の値を出力してください。
なお、n は 1≦n≦7を満たす整数とします。

【入出力サンプル】
標準入力
3

標準出力
8

===================================

R で，簡単に書ける。が，n = 7 のときは 6 秒ほどかかるので，後で Java で書き換える。

F = function(n) {
    G = function(X) {
        for (k in 1:nrow(p)) {
            x = X[p[k,]]
            if (sum(x * weight) >= Min) {
                next
            }
            a[1, ] = x
            for (i in 2:n) {
                for (j in 1:(n-i+1)) {
                    a[i, j] = a[i - 1, j] + a[i - 1, j+1]
                }
            }
            result = a[n, 1]
            if (result < Min && length(unique(a[a!=0])) == elements) {
                Min = result
            }
        }
        Min
    }
    elements = n*(n+1)/2
    Min = 1e10
    library(e1071)
    p = permutations(n)
    a = matrix(0, n, n)
    x = combn(13, n)
    x = x[, x[1,] == 1]
    x = x[, x[2,] == 2]
    weight = choose(n-1, 0:(n-1))
    for (i in 1:ncol(x)) {
        Min = min(Min, G(x[,i]))
    }
    cat(Min)
}

> system.time(F(3)) # 8
8   ユーザ   システム       経過  
     0.043      0.002      0.045
> system.time(F(4)) # 20
20   ユーザ   システム       経過  
     0.004      0.000      0.003
> system.time(F(5)) # 43
43   ユーザ   システム       経過  
     0.066      0.003      0.068
> system.time(F(6)) # 98, 0.961 seq.
98   ユーザ   システム       経過  
     0.524      0.007      0.521
> system.time(F(7)) # 212, 6.095 sec.
212   ユーザ   システム       経過  
     5.822      0.052      5.850

計算処理時間対策のため，Java に移植。
あっという間に計算が終わる。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        String line;
        line = cin.nextLine();
        int n = Integer.parseInt(line);
        System.out.println(F(n));
    }

    static int G(int Min, int n, int [] weight, int [] X, int [][] p) {
        int i, j, k;
        int result;
        int [] x = new int[n+1];
        int nrow = p.length;
        int [][] a = new int[n+1][n+1];
        int [] check = new int[n*(n+1)/2];
        int m;
        boolean dup;
        for (k = 1; k < nrow; k++) {
            int sum = 0;
            for (j = 1; n >= j; j++) {
                x[j] = X[p[k][j]];
                sum += x[j]*weight[j];
            }
            if (sum >= Min) continue;
            for (j = 1; n >= j; j++) {
                a[1][j] = x[j];
            }
            for (i = 2; n >= i; i++) {
                for (j = 1; n-i+1 >= j; j++) {
                    a[i][j] = a[i-1][j]+a[i-1][j+1];
                }
            }
            result = a[n][1];
            m = 0;
            for (i = 1; n >= i; i++) {
                for (j = 1; n-i+1 >= j; j++) {
                    check[m++] = a[i][j];
                }
            }
            dup = false;
            for (i = 0; i < check.length-1; i++) {
                for (j = i+1; j < check.length; j++) {
                    if (check[i] == check[j]) {
                        dup = true;
                        break;
                    }
                }
                if (dup == true) break;
            }
            if (dup == false) {
                Min = result;
            }
        }
        
        return Min;
    }

    static int F(int n) {
        int elements = n * (n + 1) / 2;
        int [] weight = new int[n+2];
        int Min = 1000000000;
        int MAX = 15; // 実際には MAX = 13 で O.K.
        int    [][] p = permutations(n);
        int [] vec = new int[MAX+1];
        int [] y = new int[n+1];
        int i, j;
        for (i = 1; MAX >= i; i++) {
            vec[i] = i;
        }
        for (i = 1; n >= i; i++) {
            weight[i] = (int) (factorial(n-1) / factorial(i-1) / factorial(n-i));
        }
        int [][] x = combn(vec, MAX, n);
        int cols = (int) (factorial(MAX) / factorial(n) / factorial(MAX-n));
        for (i = 1; cols >= i; i++) {
            for (j = 1; n >= j; j++) {
                y[j] = x[j][i];
            }
            Min = Math.min(Min, G(Min, n, weight, y, p));
        }
        return Min;
    }

    static double factorial(int n) {
        int i;
        double result = 1;
        for (i = 1; n >= i; i++) {
            result *= i;
        }
        return result;
    }

    static int[][] permutations(int n) {
        int sizeZ = (int)factorial(n);
        int sizeX = sizeZ / (n - 1);
        int[][] z = new int[sizeZ + 1][n + 1];
        int[][] x = new int[sizeX + 1][n + 1];
        int nrowZ, ncolZ, nrowX, ncolX;
        int i, i2, j, j2;
        z[1][1] = 1;
        nrowZ = ncolZ = 1;
        for (i = 2; n >= i; i++) {
            for (i2 = 1; nrowZ >= i2; i2++) {
                for (j2 = 1; ncolZ >= j2; j2++) {
                    x[i2][j2] = z[i2][j2];
                }
                x[i2][ncolZ + 1] = i;
            }
            nrowX = nrowZ;
            ncolX = ncolZ + 1;
            for (j = 1; i >= j; j++) {
                for (j2 = 1; nrowX >= j2; j2++) {
                    for (i2 = 1; ncolX >= i2; i2++) {
                        z[(j - 1) * nrowX + j2][i2] = x[j2][(j + i2 - 2) % i
                                + 1];
                    }
                }
            }
            nrowZ = i * nrowX;
            ncolZ = ncolX;
        }

        return z;
    }

    static int[][] combn(int[] x, int n, int m) {
        int e, h, i, j, nmmp1, lenr;
        int[] a = new int[m + 1];
        int[] r = new int[m + 1];
        int count = (int) (factorial(n) / factorial(m) / factorial(n - m));
        int[][] out = new int[m + 1][count + 1];
        e = 0;
        h = m;
        for (i = 1; m >= i; i++) {
            a[i] = i;
            r[i] = x[i];
        }
        lenr = r.length - 1;
        for (j = 1; count >= j; j++) {
            for (i = 1; lenr >= i; i++) {
                out[i][j] = r[i];
            }
        }
        i = 2;
        nmmp1 = n - m + 1;
        while (a[1] != nmmp1) {
            if (e < n - h) {
                h = 1;
                e = a[m];
            } else {
                e = a[m - h];
                h++;
            }
            for (j = 1; h >= j; j++) {
                a[m - h + j] = e + j;
            }
            for (j = 1; m >= j; j++) {
                out[j][i] = x[a[j]];
            }
            i++;
        }
        return out;
    }
}