和算の心(その009)
円の直径,弦,矢の関係式を「径矢弦の定理」と呼ぶことがある。

直角三角形 OBD において,ピタゴラスの定理(三平方の定理)を適用する。
OB² + BD² = OD²
(径/2 - 矢)² + (弦/2)² = (径/2)²
方程式:(径/2 - 矢)^2 + (弦/2)^2 - (径/2)^2 は,径,矢,弦のうちの 2 つが与えられると,残りの 1 つが計算できる。
include("julia-source.txt");
@syms 径::posiitive, 矢::positive, 弦::positiiive
eq = (径/2 - 矢)^2 + (弦/2)^2 - (径/2)^2
径,矢がわかっているときに,弦を求める。
2 通りの解が得られるが,正のものが適解である。
弦 = 2*sqrt(矢)*sqrt(径 - 矢)
ans_弦 = solve(eq, 弦)
ans_弦 |> println
Sym{PyCall.PyObject}[-2*sqrt(矢)*sqrt(径 - 矢), 2*sqrt(矢)*sqrt(径 - 矢)]
径,弦が分かっているときに,矢を求める。
2 通りの解が得られる。小さい方が「矢」,大きい方は「大矢」と呼ばれることもある。「矢 + 大矢 = 径」である。
矢 = 径/2 - sqrt(-弦^2 + 径^2)/2
大矢 = 径/2 + sqrt(-弦^2 + 径^2)/2
ans_矢 = solve(eq, 矢)
ans_矢 |> println
Sym{PyCall.PyObject}[径/2 - sqrt(-弦^2 + 径^2)/2, 径/2 + sqrt(-弦^2 + 径^2)/2]
矢,弦が分かっているときに,径を求める。
径 = 弦^2/(4*矢) + 矢
ans_径 = solve(eq, 径)
ans_径 |> println
Sym{PyCall.PyObject}[弦^2/(4*矢) + 矢]
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
弦 = 0.8
径 = 1
矢 = 径/2 - sqrt(-弦^2 + 径^2)/2
矢2 = 径/2 + sqrt(-弦^2 + 径^2)/2
@printf("弦 = %g, 径 = %g のとき,矢 = %g, 大矢 = %g\n", 弦, 径, 矢, 矢2)
径 = 1
矢 = 0.2
弦 = 2*sqrt(矢*(径 - 矢))
@printf("径 = %g, 矢 = %g のとき,弦 = %g\n", 径, 矢, 弦)
矢 = 0.2
弦 = 0.8
径 = 弦^2/(4*矢) + 矢
@printf("矢 = %g, 弦 = %g のとき,径 = %g\n", 矢, 弦, 径)
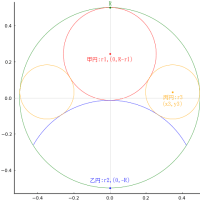
plot()
circle(0, 0, 径/2)
segment(-弦/2, 径/2 - 矢, 弦/2, 径/2 - 矢)
segment(-径/2, 0, 径/2, 0, :blue)
segment(0, 径/2, 0, 径/2 - 矢, :green)
segment(0, 0, 0, 径/2 - 矢, :orange)
segment(0, 0, 弦/2, 径/2 - 矢, :magenta)
if more == true
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
#hline!([0], color=:gray80, lw=0.5)
#vline!([0], color=:gray80, lw=0.5)
point(径/4, 径/4 - 矢/2, "OD:径/2", :magenta, :center, delta=-delta, mark=false)
point(-径/4, 0, "EF:径(直径)", :blue, :center, delta=-delta, mark=false)
point(-弦/4, 径/2 - 矢, " CD=弦", :black, :center, delta=-delta, mark=false)
point(弦/4, 径/2 - 矢, " BD=弦/2", :black, :center, delta=-delta, mark=false)
point(0, 径/2 - 矢/2, " AB:矢", :green, :left, delta=-delta/2, mark=false)
point(0, 径/2 - 3矢/2, "OB:径/2-矢 ", :orange, :right, delta=-delta/2, mark=false)
point(0, 径/2, "A", :black, :center, :bottom, delta=delta/2)
point(0, 径/2 - 矢, "B ", :black, :right, :bottom, delta=delta/2)
point(-弦/2, 径/2 - 矢, "C", :black, :right, :bottom, delta=delta/2)
point(弦/2, 径/2 - 矢, "D", :black, :left, :bottom, delta=delta/2)
point(-径/2, 0, "E ", :black, :right, :bottom, delta=delta/2)
point(径/2, 0, " F", :black, :left, :bottom, delta=delta/2)
point(0, 0, "O", :black, :center, delta=-delta)
xlims!(-径/2 - 5delta, 径/2 + 5delta)
end
end;
draw(true)