算額(その1430)
八十九 陸前高田市小友町 常膳寺観音堂 天保13年(1842)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円12個,外円,正三角形3個
#Julia, #SymPy, #算額, #和算
正三角形の中に斜線を 2 本,全円 1 個,甲円 1 個,乙円 3 個,全円 1 個を容れる。甲円の直径が与えられたとき,丙円の直径を得る術を述べよ。
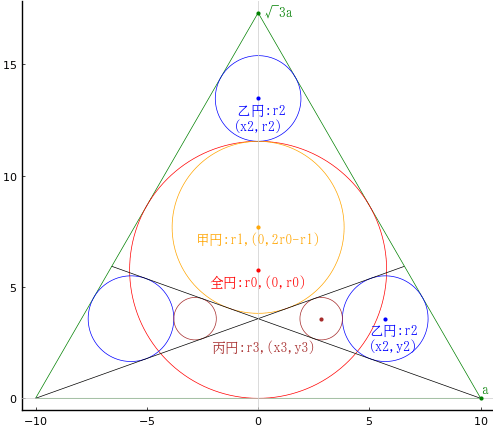
正三角形の一辺の長さを 2a
甲円の半径と中心座標を r1, (0, 2r0 - r1)
乙円の半径と中心座標を r2, (x2, y2), (0, 2r0 + r2)
丙円の半径と中心座標を r3, (x3, y3)
全円の半径と中心座標を r0, (0, r0)
とおき,以下の連立方程式を解く。
なお,r0 = √3a/3, r2 = √3a/9, y3 = y2 である。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms a, r0, r1, r2, x2, y2, r3, x3, y3, b
# eq1 = r0 - a/√Sym(3)
# eq2 = 2r2 - (√Sym(3)a - 2r0 - r2)
# res = solve([eq1, eq2], (r0, r2))
# r0 = √Sym(3)a/3
# r2 = √Sym(3)a/9
r0 = √Sym(3)a/3
r2 = √Sym(3)a/9
y3 = y2
# dist2() は使えない
eq3 = dist(-a, 0, b, √Sym(3)*(a - b), x2, y2) - r2^2
eq4 = dist(-a, 0, b, √Sym(3)*(a - b), 0, 2r0 - r1) - r1^2
eq5 = dist(a, 0, -b, √Sym(3)*(a - b), x2, y2) - r2^2
eq6 = dist(a, 0, 0, √Sym(3)a, x2, y2) - r2^2
eq7 = dist(-a, 0, b, √Sym(3)*(a - b), x3, y3) - r3^2
eq8 = (x2 - x3) - (r2 + r3);
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return Float64.(v), r.f_converged
end;
function H(u)
(x2, y2, r1, b, r3, x3) = u
return [
-a^2/27 + (y2 - sqrt(3)*(a - b)*(sqrt(3)*y2*(a - b) + (a + b)*(a + x2))/(3*(a - b)^2 + (a + b)^2))^2 + (a + x2 - (a + b)*(sqrt(3)*y2*(a - b) + (a + b)*(a + x2))/(3*(a - b)^2 + (a + b)^2))^2, # eq3
-r1^2 + (a - (a + b)*(a*(a + b) + sqrt(3)*(a - b)*(2*sqrt(3)*a/3 - r1))/(3*(a - b)^2 + (a + b)^2))^2 + (2*sqrt(3)*a/3 - r1 - sqrt(3)*(a - b)*(a*(a + b) + sqrt(3)*(a - b)*(2*sqrt(3)*a/3 - r1))/(3*(a - b)^2 + (a + b)^2))^2, # eq4
-a^2/27 + (y2 - sqrt(3)*(a - b)*(sqrt(3)*y2*(a - b) + (-a - b)*(-a + x2))/((-a - b)^2 + 3*(a - b)^2))^2 + (-a + x2 - (-a - b)*(sqrt(3)*y2*(a - b) + (-a - b)*(-a + x2))/((-a - b)^2 + 3*(a - b)^2))^2, # eq5
-a^2/27 + (y2 - sqrt(3)*a*(sqrt(3)*a*y2 - a*(-a + x2))/(4*a^2))^2 + (-a + x2 + a*(sqrt(3)*a*y2 - a*(-a + x2))/(4*a^2))^2, # eq6
-r3^2 + (y2 - sqrt(3)*(a - b)*(sqrt(3)*y2*(a - b) + (a + b)*(a + x3))/(3*(a - b)^2 + (a + b)^2))^2 + (a + x3 - (a + b)*(sqrt(3)*y2*(a - b) + (a + b)*(a + x3))/(3*(a - b)^2 + (a + b)^2))^2, # eq7
-sqrt(3)*a/9 - r3 + x2 - x3, # eq8
]
end;
a = 10
r0 = √3a/3 # a*0.5773502691896257
r2 = √3a/9 # a*0.19245008972987523
iniv = BigFloat[0.575411, 0.34912, 0.387466, 0.662547, 0.095137, 0.284131] .* a
res = nls(H, ini=iniv)
([5.711594854986474, 3.5787338000056996, 3.8641388667743293, 6.575250125060548, 0.9544492311458473, 2.832644726541875], true)
正三角形の一辺の長さが 2a = 20 のとき,
全円の半径 r0 = 5.773502691896257
甲円の半径 r1 = 3.8641388667743293
乙円の半径 r2 = 1.9245008972987523
丙円の半径 r3 = 0.9544492311458473
丙円の直径/甲円の直径 = 0.9544492311458473/3.8641388667743293 = 0.2470017936862072
甲円の直径/丙円の直径 = 3.8641388667743293/0.9544492311458473 = 4.048553595810754
術は,「15572 の平方根から 121 を引き,甲円の直径を掛ければ全円の直径がえられる」とあるが,√15572 - 121 = 3.787819918451973 であり,題意を満たさない。
function draw(a, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x2, y2, r1, b, r3, x3) = [5.711594854986474, 3.5787338000056996, 3.8641388667743293, 6.575250125060548, 0.9544492311458473, 2.832644726541875]
y3 = y2
r0 = √3a/3
r2 = √3a/9
plot([a, 0, -a, a], [0, sqrt(3)a, 0, 0], color=:green, lw=0.5)
circle(0, a/sqrt(3), r0)
circle(0, 2r0 + r2, r2, :blue)
circle2(x2, y2, r2, :blue)
circle2(x3, y3, r3, :brown)
circle(0, 2r0 - r1, r1, :orange)
segment(-a, 0, b, (a - b)*√3)
segment(a, 0, -b, (a - b)*√3)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, √3a, " √3a", :green, :left, :vcenter)
point(a, 0, "a", :green, :left, :bottom, delta=delta/2)
point(0, r0, "全円:r0,(0,r0)", :red, :center, delta=-delta)
point(0, 2r0 - r1, "甲円:r1,(0,2r0-r1)", :orange, :center, delta=-delta)
point(x2, y2, "乙円:r2\n(x2,y2)", :blue, :left, delta=-delta, deltax=-3delta)
point(0, 2r0 + r2, " 乙円:r2\n(x2,r2)", :blue, :center, delta=-delta)
point(x3, y3, "丙円:r3,(x3,y3)", :brown, :right, delta=-4delta, deltax=-delta)
end
end;
draw(10, true)