三角形に分割しよう

三角形に分割しよう

締め切りが 2018/01/31 10:00 AM なので，その 1 分後に投稿されるように予約

三次元のグラフィックにおいて、立体的な形状を、メッシュと呼ばれる多数の三角形で表現します。

ここでは平面に与えられる多角形を対角線で分割して、三角形を組み合わせて表現されるようにします。
このとき、切断する対角線の長さの和が最小になるような切り方を求め、その対角線の長さの和を求めてください。

下図のような場合、緑の対角線とオレンジの対角線が考えられますが、緑の方が短いので、この長さが最小になります。

各頂点の座標は整数で与えられるものとし、最大10個が入力されます。

答えは小数第三位を四捨五入して小数第二位まで求めてください。
（ヒント：対角線の長さは三平方の定理で求めることができます。）

例えば、以下の入力が与えられる下図のような五角形の場合、図にある緑の対角線の長さを合計して、答えは「4.47」となります。
（与えられた順に線をつなぎ、最後の点と最初の点をつなぐものとします）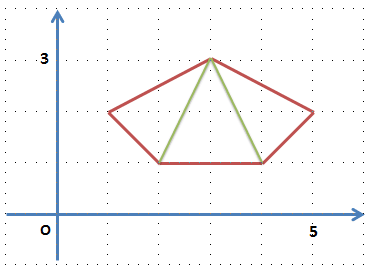

【入力】
1,2
2,1
4,1
5,2
3,3


なお、今回は凸多角形のみ対象とし、切断する対角線は頂点以外の場所で交差しないものとします。

============================================

f = function(x, y) {
  ans = Inf
  n = length(x) # 頂点数
  begin = end = integer(n*(n-3)/2) # 可能な対角線の始点と終点番号の対 1〜n
  m = n-3 # 実際に引かれる対角線の本数
  count = 0 # count = n*(n-3)/2 になる
  for (i in 1:(n-2)) {
    for (j in (i+2):(n-(i==1))) {
      count = count+1
      begin[count] = i
      end[count] = j
    }
  }
  # count 本の対角線から m 本の対角線を選び，内部で交差しないものを探す
  comb = combn(count, m)
  for (k in 1:ncol(comb)) {
    ok = TRUE
    for (i in 1:(m-1)) {
      for (j in (i+1):m) {
        if (!((begin[comb[i,k]] <= begin[comb[j,k]] && end[comb[j,k]] <= end[comb[i,k]]) ||
            (begin[comb[j,k]] <= begin[comb[i,k]] && end[comb[i,k]] <= end[comb[j,k]]) ||
            begin[comb[i,k]] >= end[comb[j,k]] ||
            begin[comb[j,k]] >= end[comb[i,k]])) {
          ok = FALSE
          break
        }
      }
      if (!ok) {
        break
      }
    }
    if (ok) {
      Length = 0
      for (i in 1:m) {
         Length = Length + sqrt((x[begin[comb[i,k]]] - x[end[comb[i,k]]])^2 +
            (y[begin[comb[i,k]]] - y[end[comb[i,k]]])^2)
      }
      ans = min(ans, Length)
    }
  }
  cat(round(ans, 2), "\n")
}
#arg = matrix(scan(file("stdin", "r"), sep=","), byrow=TRUE, ncol=2)
#f(arg[,1], arg[,2])

#f(c(1,2,4,5,3), c(2,1,1,2,3)) # 4.47
#f(c(0,1,3,4,2), c(1,0,0,1,2)) # 4.47
#system.time(f(c(0,2,3,3,2,0), c(1,0,1,3,4,3))) # 9.61
#system.time(f(c(0,1,2,3,3,2,1,0), c(1,0,0,1,2,3,3,2))) # 12.11, 0.133 s

Python3 に書き直してみる

import numpy as np
import itertools

def f(x, y):
    ans = np.Inf
    n = len(x) # 頂点数
    m = n-3 # 実際に引かれる対角線の本数
    begin = np.zeros(n*(n-3)/2) # 可能な対角線の始点番号 0〜n-1
    end = np.zeros(n*(n-3)/2)   # 可能な対角線の終点番号 0〜n-1
    count = 0 # count = n*(n-3)/2 になる
    for i in range(0, n-1):
        for j in range(i+2, n):
            if i != 0 or j != n-1:
                begin[count] = i
                end[count] = j
                count += 1
    # count 本の対角線から m 本の対角線を選び，内部で交差しないものを探す
    comb = list(itertools.combinations(range(count), m))
    for k in range(len(comb)):
        cb = comb[k]
        ok = True
        for i in range(m-1):
            for j in range(i+1, m):
                if not ((begin[cb[i]] <= begin[cb[j]] and end[cb[j]] <= end[cb[i]]) or
                (begin[cb[j]] <= begin[cb[i]] and end[cb[i]] <= end[cb[j]]) or
                begin[cb[i]] >= end[cb[j]] or begin[cb[j]] >= end[cb[i]]):
                    ok = False
                    break
            if not ok:
                break
        if ok:
            Length = 0
            for i in range(m):
                Length += np.sqrt((x[int(begin[cb[i]])] - x[int(end[cb[i]])])**2 +
                (y[int(begin[cb[i]])] - y[int(end[cb[i]])])**2)
            ans = min(ans, Length)
    print(round(ans, 2))

#f([1, 2, 4, 7, 8, 6, 3], [6, 4, 3, 3, 5, 8, 9]) # 19.49
#f([1,2,4,5,3], [2,1,1,2,3]) # 4.47
#f([0,1,3,4,2], [1,0,0,1,2]) # 4.47
#f([0,2,3,3,2,0], [1,0,1,3,4,3]) # 9.61
#f([0,1,2,3,3,2,1,0], [1,0,0,1,2,3,3,2]) # 12.11

def get_input():
    while True:
        try:
            yield ''.join(input())
        except EOFError:
            break

a = list(get_input())
x = np.zeros(len(a))
y = np.zeros(len(a))
for i in range(len(a)):
    b = a[i].split(",")
    x[i] = b[0]
    y[i] = b[1]
f(x, y)
# 1,2
# 2,1
# 4,1
# 5,2
# 3,3  # 4.47