算額(その1530)
四十四 岩手県一関市真滝 熊野白山滝神社 文久元年(1861)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
今有如図 03048
https://w.atwiki.jp/sangaku/pages/195.html
キーワード:円7個,外円
#Julia, #SymPy, #算額, #和算
山村は,「問・答・術は読めない」としているが,「今有如図」では問・答・術が記載されている。
問:今有全円内如図設至多大円二個容小円四個小円径一寸問大円径幾何
答:曰至多大円径二寸九分六厘有奇
術:術曰置八個開平方加三個二分五厘開平方加五
分乗小円径得至多大円径合問
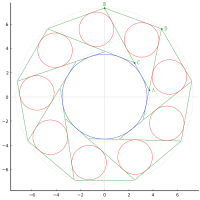
全円の中に,大円 2 個,小円 4 個を容れる。小円の直径が 1 寸のとき,大円の直径が最大になるときの大円の直径はいかほどか。

大円の直径が最大になるのは全円の直径の 1/2 のときである。また,小円は 2 個ずつグループを作りそれぞれは大円に外接し,隣同士の小円も外接し合っている(村山の図はこの点については不正確)。
以上のような前提で求めた解は答・術に一致した。
全円の半径と中心座標を R, (0, 0); R = 2r1
大円の半径と中心座標を r1, (r1, 0)
小円の半径と中心座標を r2, (r2, y21), (x2, y22)
とおき,以下の連立方程式を解く。
include("julia-source.txt")
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positive, y21::negative, y22::negative
R = 2r1
eq1 = x2^2 + y22^2 - (R - r2)^2
eq2 = (r1 - r2)^2 + y21^2 - (r1 + r2)^2
eq3 = (r1 - x2)^2 + y22^2 - (r1 + r2)^2
eq4 = (x2 - r2)^2 + (y21 - y22)^2 - 4r2^2
res = solve([eq1, eq2, eq3, eq4], (r1, x2, y21, y22))[1]
(r2*(1 + sqrt(8*sqrt(2) + 13))/2, r2*(-2 + sqrt(8*sqrt(2) + 13)), 2*r2*(-2 - sqrt(2))/sqrt(-1 + sqrt(8*sqrt(2) + 13)), -2*r2*sqrt(-1 + sqrt(8*sqrt(2) + 13)))
大円の半径 r1 は,小円の半径 r2 の (1 + sqrt(8√2 + 13))/2 倍である。
「術」は (sqrt(√8 + 3.25) + 0.5) で一致する。
小円の直径が 1 のとき,大円の直径は 2.965446637983915 であり,「答」と一致する。
function draw(r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, x2, y21, y22) = (r2*(1 + sqrt(8*sqrt(2) + 13))/2, r2*(-2 + sqrt(8*sqrt(2) + 13)), 2*r2*(-2 - sqrt(2))/sqrt(-1 + sqrt(8*sqrt(2) + 13)), -2*r2*sqrt(-1 + sqrt(8*sqrt(2) + 13)))
R = 2r1
@printf("r2 = %g; r1 = %g\n", 2r2, 2r1)
plot()
circle(0, 0, R, :green)
circle2(r1, 0, r1)
circle2(r2, y21, r2, :blue)
circle2(x2, y22, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :green, :center, :bottom, delta=delta)
point(r1, 0, "大円:r1,(r1,0)", :red, :center, delta=-delta)
point(r2, y21, "小円:r2\n(r2,y21)", :blue, :center, delta=-delta)
point(x2, y22, "小円:r2\n(x2,y22)", :blue, :center, delta=-delta)
end
end;
draw(1/2, true)