算額（その1380）

算額（その1380）

一七 大里郡岡部村岡 稲荷社 文化13年(1816)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：直角三角形，中鈎，正方形
#Julia, #SymPy, #算額, #和算

問：只云大積四寸小積一寸問方積

非常に短く書かれているが，もう少し分かりやすく書き直す。
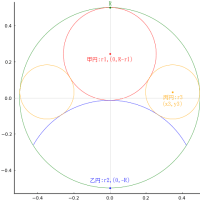
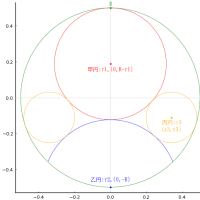
直角三角形の中に正方形を容れる。直角三角形の直角を挟む二辺の短い方を鈎，長い方を股，斜辺を弦と呼ぶ。直角の頂点から弦へおろした垂線を中鈎と呼ぶ。中鈎と弦の交点座標により区分される弦の短い方を短弦，長い方を長と弦呼ぶ。短弦と中鈎で構成される直角三角形の面積を小積，長弦と中鈎で構成される直角三角形の面積を大積と呼ぶ。大積が 4 平方寸(注1），小積が 1 平方寸のとき，正方形の一辺の長さはいかほどか。

注1：当時は，単位の次元の概念がなかった。「寸」×「寸」は「平方寸」であるが，「寸」と表していた。
注2：大積，小積の定義は明記されていないが，図に「中鈎」が描かれているので，短弦，長弦を底辺，中鈎を高さとする直角三角形の面積と解釈した。

正方形の一辺の長さを a
鈎，股，弦，短弦，長弦，中鈎に対する変数をそのまま，「鈎」，「股」，「弦」，「短弦」，「長弦」，「中鈎」
大積，小積を K1, K2
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive, 短弦::positive, 長弦::positive,
     中鈎::positive, x0::positive, y0::positive, a::positive, K1::positive, K2::positive
eq1 = 短弦/中鈎 - 鈎/股
eq2 = 中鈎/長弦 - 鈎/股
eq3 = 鈎^2 + 股^2 - 弦^2
eq4 = 短弦 + 長弦 - 弦
eq5 = 長弦*中鈎/2 - K1  # 大積
eq6 = 短弦*中鈎/2 - K2  # 小積
eq7 = (鈎 - a)/a - a/(股 - a)  # 正方形により区分される 2 つの直角三角形は相似であること
eq8 = sqrt(x0^2 + y0^2) - 中鈎
eq9 = (鈎 - y0)/x0 - y0/(股 - x0)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9],
   (a, 鈎, 股, 弦, 短弦, 長弦, 中鈎, x0, y0))[1]

   (K1^(1/4)*K2^(1/4)*(sqrt(K1) - sqrt(K2))*sqrt(2*K1 + 2*K2)/(K1 - K2), K2^(1/4)*sqrt(2*K1 + 2*K2)/K1^(1/4), K1^(1/4)*sqrt(2*K1 + 2*K2)/K2^(1/4), sqrt(2)*(K1 + K2)/(K1^(1/4)*K2^(1/4)), sqrt(2)*K2^(3/4)/K1^(1/4), sqrt(2)*K1^(3/4)/K2^(1/4), sqrt(2)*K1^(1/4)*K2^(1/4), sqrt(2)*K1^(1/4)*K2^(3/4)/sqrt(K1 + K2), sqrt(2)*K1^(3/4)*K2^(1/4)/sqrt(K1 + K2))

for i = 1:9
   println("$i: $(res[i](K1 => 4, K2 => 1).evalf())")
end

   1: 1.49071198499986
   2: 2.23606797749979
   3: 4.47213595499958
   4: 5.00000000000000
   5: 1.00000000000000
   6: 4.00000000000000
   7: 2.00000000000000
   8: 0.894427190999916
   9: 1.78885438199983

正方形の一辺の長さ

res[1] |> println
res[1](K1 => 4, K2 => 1) |> println
res[1](K1 => 4, K2 => 1).evalf() |> println

   K1^(1/4)*K2^(1/4)*(sqrt(K1) - sqrt(K2))*sqrt(2*K1 + 2*K2)/(K1 - K2)
   2*sqrt(5)/3
   1.49071198499986

正方形の面積

S = res[1]^2
S |>  println
S(K1 => 4, K2 => 1) |> println
S(K1 => 4, K2 => 1).evalf() |> println

   sqrt(K1)*sqrt(K2)*(sqrt(K1) - sqrt(K2))^2*(2*K1 + 2*K2)/(K1 - K2)^2
   20/9
   2.22222222222222

短弦 = 1, 中鈎 = 2, 小積 = 1
長弦 = 4, 中鈎 = 2, 大積 = 4
正方形の一辺の長さ = 1.49071, 面積 = 2.22222

全てのパラメータは以下のとおりである。
K1 = 4;  K2 = 1;  a = 1.49071;  鈎 = 2.23607;  股 = 4.47214;  弦 = 5;  短弦 = 1;  長弦 = 4;  中鈎 = 2;  x0 = 0.894427;  y0 = 1.78885

function draw(K1, K2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, 鈎, 股, 弦, 短弦, 長弦, 中鈎, x0, y0) = (K1^(1/4)*K2^(1/4)*(sqrt(K1) - sqrt(K2))*sqrt(2*K1 + 2*K2)/(K1 - K2), K2^(1/4)*sqrt(2*K1 + 2*K2)/K1^(1/4), K1^(1/4)*sqrt(2*K1 + 2*K2)/K2^(1/4), sqrt(2)*(K1 + K2)/(K1^(1/4)*K2^(1/4)), sqrt(2)*K2^(3/4)/K1^(1/4), sqrt(2)*K1^(3/4)/K2^(1/4), sqrt(2)*K1^(1/4)*K2^(1/4), sqrt(2)*K1^(1/4)*K2^(3/4)/sqrt(K1 + K2), sqrt(2)*K1^(3/4)*K2^(1/4)/sqrt(K1 + K2))
   @printf("短弦 = %g, 中鈎 = %g, 小積 = %g\n", 短弦, 中鈎, 短弦*中鈎/2)
   @printf("長弦 = %g, 中鈎 = %g, 大積 = %g\n", 長弦, 中鈎, 長弦*中鈎/2)
   @printf("正方形の一辺の長さ = %g, 面積 = %g\n", a, a^2)
   @printf("K1 = %g;  K2 = %g;  a = %g;  鈎 = %g;  股 = %g;  弦 = %g;  短弦 = %g;  長弦 = %g;  中鈎 = %g;  x0 = %g;  y0 = %g\n", K1, K2, a, 鈎, 股, 弦, 短弦, 長弦, 中鈎, x0, y0)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   rect(0, 0, a, a, :red)
   segment(0, 0, x0, y0, :green)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, a, "(a,a)", :red, :left, :bottom, delta=delta/2)
       point(x0, y0, "(x0,y0)", :green, :left, :bottom, delta=delta/2)
       point(股, 0, "股", :blue, :left, :bottom, delta=delta)
       point(0, 鈎, " 鈎", :blue, :left, :bottom, delta=delta)
       point(x0/2, y0/2, "中鈎", :green, mark=false)
   end
end;

draw(4, 1, true)