算額（その856）

算額（その856）

二十二　岩手県一関市瑞山 駒形根神社 明治41年(1908)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

外円内に大円 2 個，小円 6 個が入っている。外円の直径が 10 寸のとき，小円の直径を得る術を問う。

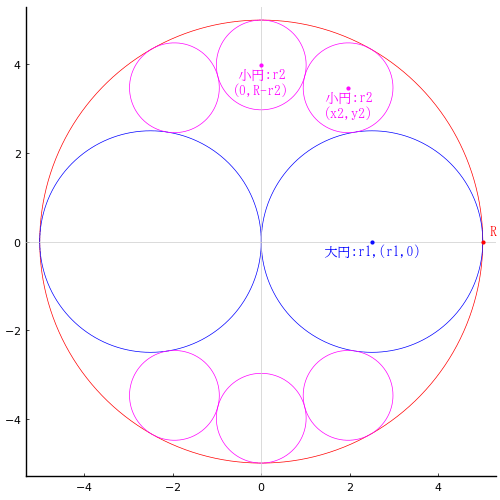
外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (r1, 0)
小円の半径と中心座標を r2, (0, R - r2), (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R, r1, r2, x2, y2
r1 = R/2
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = (r1 - x2)^2 + y2^2 - (r1 + r2)^2
eq3 = x2^2 + (R - r2 - y2)^2 - 4r2^2;
res = solve([eq1, eq2, eq3], (r2, x2, y2));

4 組の解が得られるが，2 番目のものが適解である。

(res[2][1](R=>5).evalf(),
res[2][2](R=>5).evalf(),
res[2][3](R=>5).evalf())

   (1.01331143350161, 1.96006569949517, 3.47157430856830)

それぞれは非常に長い式であるが，R が与えられれば小円の直径を求める「術」はある。以下のように計算すればよい。

# res[2][1] を求める関数を定義する

function 直径(R)
   f = ∛2
   h = f^2
   m = √69
   e = 69m + 997
   c = ∛e
   b = c^2
   a = 3h*b
   d = 330f + 37*c + a
   g = √d
   i = ∜d
   j = e^(5/6)
   k = d^(3/4)
   s = √e
   q = e^(1/6)
   r = (138m + 1994)^(2/3)
   n = sqrt(-a*g - 330f*g + 430*s + 74*c*g)
   o = sqrt(-207h*b*g - 22770f*g + 29670s + 5106c*g)
   p = sqrt(22770f + 2553c + 207h*b)
   R*(-17750573f*b*k*n/1242 - 154556461h*c*k*n/1242 - 2602054165k*n/1242 - 214763h*c*k*o/18 - 3923195k*o/18 - 21809f*b*k*o/18 - 4907453r*g/2 - 1625993r*p/6 - 341870903*c*g/9 - 11855327c*p/3 - 171811097f*g - 48431557f*p/3 + 658961h*m*s*i*n/9 + 28361659q*i*o/18 + 83669f*j*i*o/9 + 494602117h*s*i*n/621 + 18810834773q*i*n/1242 + 64451243f*j*i*n/621 + 8457376h*m*j + 488797196sqrt(4761*m + 68793)/3 + 1660341296f*m*q + 14095396844s/9 + 45213761744f*q/3 + 268114864h*j/3)/(19029096h*m*j + 366597897*m*s + 3735767916f*m*q + 3523849211s + 33910321308f*q + 201086148h*j)
end;
直径(10/2)

   1.01331143350161

算額では「術」はなく「答」も天下り式に「小円二寸」とある。
山村の記述では，「外円径÷5 = 小円径」としているが，こじつけである。

何度も経験することであるが，この文書に収められている算額および山村の記述には問題が多い。

function draw(more=false)
   pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10/2
   r1 = R/2
   (r2, x2, y2) = (1.01331143350161, 1.96006569949517, 3.47157430856830)
   plot()
   circle(0, 0, R)
   circle2(r1, 0, r1, :blue)
   circle22(0, R - r2, r2, :magenta)
   circle4(x2, y2, r2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(r1, 0, "大円:r1,(r1,0)", :blue, :center, delta=-delta/2)
       point(0, R - r2, "小円:r2\n(0,R-r2)", :magenta, :center, delta=-delta/2)
       point(x2, y2, "小円:r2\n(x2,y2)", :magenta, :center, delta=-delta/2)
   end
end;