算額(その1542)
四十 埼玉県熊谷市玉井 玉井大神社 嘉永元年(1848)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
山口正義:やまぶき 第 4 号
https://yamabukiwasan.sakura.ne.jp/ymbk4.pdf
キーワード:正五角形,面積分割
#Julia, #SymPy, #算額, #和算
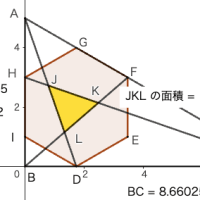
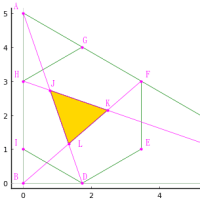
正五角形の一辺が 1 寸のとき,この面積を三等分するときの截面(一辺の分割した長さ;図参照)はいかほどか。

計算しなくても,図を見ればわかる。
四角形OAEB = 五角形OECDE' ならば,三角形OBE が三角形OCE の二倍,すなわち CE が BC の 1/3 である。
あえて計算すると,以下のようになる。
正五角形が内接する円の半径を r,一辺の長さを「五角面」,截面を「截面」とおき,以下の連立方程式を解く。
include("julia-source.txt");
# # julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
@syms r, x, y, 五角面
s18 = Sym(18)
s36 = Sym(36)
r = 五角面/2sind(s36)
S = r^2*sind(s36)*cosd(s36) # 正五角形の面積/5
s1 = area([0 0; r*cosd(s18) r*sind(s18); x y]) # 面積/5 の更に 2/3
s2 = area([0 0; x y; r*sind(s36) -r*cosd(s36)]) # 面積/5 の更に 1/3
eq1 = s1 - 2S/3 # S/5 + s1 = S/5 + s2
eq2 = s2 - S/3;
res = solve([eq1, eq2], (x, y));
@syms d
ans_x = apart(res[x]) |> simplify
ans_x |> println
五角面*(sqrt(5) + 5)/12
ans_y = apart(res[y]) |> simplify
ans_y|> println
-五角面*(5*sqrt(2) + 3*sqrt(10))*sqrt(sqrt(5) + 5)/120
截面 = sqrt((r*sind(s36) - ans_x)^2 + (-r*cosd(s36) - ans_y)^2) |> simplify
截面 |> println
截面(五角面 => 1).evalf() |> println
sqrt(10)*sqrt(-15*sqrt(5 - sqrt(5))*sqrt(sqrt(5) + 5) - 6*sqrt(5)*sqrt(5 - sqrt(5))*sqrt(sqrt(5) + 5) + 20*sqrt(5) + 110)*sqrt(五角面^2)/(30*sqrt(5 - sqrt(5)))
0.333333333333333
截面は五角面の 1/3 である。
function draw(五角面, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 五角面/2sind(36)
x = 五角面*(√5 + 5)/12
y = -五角面*(5√2 + 3√10)*sqrt(√5 + 5)/120
(x1, y1) = r.*(sind(36), -cosd(36))
(x2, y2) = r.*(cosd(18), sind(18))
length = sqrt((x - x1)^2 + (y - y1)^2)
@printf("正五角形の一辺の長さが %g のとき,面積を 3 分割するときの\"截面\"は %g である。\n", 五角面, length)
plot([-x, 0, x], [y, 0, y], color=:blue, lw=0.5, showaxis=false)
polygon(0, 0, r, 5, color=:red)
segment(0, 0, 0, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
# hline!([0], color=:gray80, lw=0.5)
# vline!([0], color=:gray80, lw=0.5)
point(x, y, " (x,y)", :blue, :left, :vcenter)
point(x1, y1, " (x1,y1)", :red, :left, :bottom, delta=delta/2)
dimension_line(-x1, y1 - delta, x1, y1 - delta, "五角面", :red, :center, delta=-2delta)
dimension_line(-x1 - 1.5delta, y1 - delta/2, -x - 1.5delta, y - delta/2, "截面", :magenta, :right)
segment(0, 0, -x2, y2, :gray80)
segment(0, 0, -x1, y1, :gray80)
segment(0, 0, x1, y1, :gray80)
point(0, 0, " O", :blue, :left, :bottom, delta=delta/2)
point(0, r, "A", :blue, :center, :bottom, delta=delta/2)
point(-x2, y2, "B ", :blue, :right, :vcenter)
point(-x1, y1, " C", :blue, :left, :bottom, delta=delta/2)
point(x1, y1, "D ", :blue, :right, :bottom, delta=delta/2)
point(-x, y, "E ", :blue, :right, :bottom, delta=delta/2)
point(x, y, "E' ", :blue, :right, delta=-delta/2)
end
end;
draw(1, true)