算額(その1216)
(19) 兵庫県姫路市広峯山 広峰神社 明治18年(1885)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
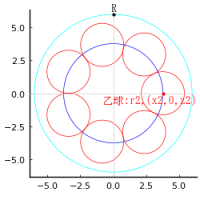
キーワード:円4個,楕円
楕円の中に,甲円 4 個,乙円 2 個を容れる。楕円の長径と短径が与えられたとき,甲円の直径はいかほどか。

注:甲円,乙円,楕円は共通接点で接する。
楕円に内接する 2 個の等円については算法助術の公式84を適用する。
楕円の長半径,短半径,中心座標を a, b, (0, 0)
甲円の半径と中心座標を r1, (r1, 0)
乙円の半径と中心座標を r2, (x2, r2)
甲円,乙円,楕円の共通接点を (x0, y0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive, r1::positive,
r2::positive, x2::positive,
x0::positive, y0::positive
eq1 = (2r1)^2/4 - (a^2 - b^2)*(b^2 - r1^2)/b^2 # 算法助術の公式84
eq2 = (x2 - r1)^2 + r2^2 - (r1 - r2)^2
eq3 = (x0 - r1)^2 + y0^2 - r1^2
eq4 = (x0 - x2)^2 + (y0 - r2)^2 - r2^2
eq5 = x0^2/a^2 + y0^2/b^2 - 1;
連立方程式を解くと,かなり長い式で表される解が得られる。
res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, x2, x0, y0))[4] # 4 0f 4
(b*(a^2 - b^2)*sqrt(1/(a - b))/(a*sqrt(a + b)), (a^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) - a^4*sqrt(a + b)*sqrt(1/(a - b)) + a^3*b*sqrt(a + b)*sqrt(1/(a - b)) - 2*a^2*b^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) + 2*a^2*b^2*sqrt(a + b)*sqrt(1/(a - b)) - 2*a*b^3*sqrt(a + b)*sqrt(1/(a - b)) + b^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))/b^3, (-a^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) + a^2*sqrt(a + b)*sqrt(1/(a - b)) - a*b*sqrt(a + b)*sqrt(1/(a - b)) + b^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))/b, a*b*sqrt(1/(a - b))/sqrt(a + b), b*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))
乙円の半径は r1 = b*(a^2 - b^2)*sqrt(1/(a - b))/(a*sqrt(a + b)) となるが,eq1 を r1 についてとくと,もう少し簡約化された解 r1 = b*sqrt(a^2 - b^2)/a が得られる。
ans_r1 = solve(eq1, r1)[1]
ans_r1 |> println
b*sqrt(a^2 - b^2)/a
甲円の式も長いものであるが,たとえば長径,短径がそれぞれ 11170 寸,4204 寸のとき,式に代入することにより甲円の直径は 1934.000000079764 寸である。
res[2] |> println
(a^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) - a^4*sqrt(a + b)*sqrt(1/(a - b)) + a^3*b*sqrt(a + b)*sqrt(1/(a - b)) - 2*a^2*b^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) + 2*a^2*b^2*sqrt(a + b)*sqrt(1/(a - b)) - 2*a*b^3*sqrt(a + b)*sqrt(1/(a - b)) + b^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))/b^3
2res[2](a => 11170/2, b => 4204/2).evalf() |> println
1934.00000007983
その他のパラメータは以下のとおりである
a = 5585; b = 2102; r1 = 1947.44280674992, r2 = 967.000000039889, x2 = 2109.24; x0 = 2268.82; y0 = 1920.74
function draw(a, b, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = b*sqrt(a^2 - b^2)/a
println("r1 = $r1")
(r1, r2, x2, x0, y0) = (b*(a^2 - b^2)*sqrt(1/(a - b))/(a*sqrt(a + b)), (a^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) - a^4*sqrt(a + b)*sqrt(1/(a - b)) + a^3*b*sqrt(a + b)*sqrt(1/(a - b)) - 2*a^2*b^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) + 2*a^2*b^2*sqrt(a + b)*sqrt(1/(a - b)) - 2*a*b^3*sqrt(a + b)*sqrt(1/(a - b)) + b^4*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))/b^3, (-a^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)) + a^2*sqrt(a + b)*sqrt(1/(a - b)) - a*b*sqrt(a + b)*sqrt(1/(a - b)) + b^2*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))/b, a*b*sqrt(1/(a - b))/sqrt(a + b), b*sqrt((a^2 - 2*b^2)/(a^2 - b^2)))
println("r1 = $r1")
@printf("長径,短径がそれぞれ %g,%g のとき,甲円の直径は %.15g 寸である。\n", 2a, 2b, 2r2)
@printf("a = %g; b = %g; r1 = %.15g, r2 = %.15g, x2 = %g; x0 = %g; y0 = %g\n", a, b, r1, r2, x2, x0, y0)
plot()
ellipse(0, 0, a, b, color=:green)
circle2(r1, 0, r1)
circle4(x2, r2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x2, r2, "甲円:r2\n(x2,r2)", :blue, :center, delta=-delta)
point(r1, 0, " 乙円:r1\n (r1,0)", :red, :center, delta=-4delta)
point(x0, y0, "(x0,y0)", :green, :left, :bottom, delta=delta)
point(a, 0, " a", :green, :left, :bottom, delta=delta)
point(0, b, " b", :green, :left, :bottom, delta=delta)
end
end;
draw(11170/2, 4204/2, true)