算額(その1610)
福島県田村市船引町門鹿宮林 古室神社 明治16年(1883)頃
http://www.wasan.jp/fukusima/komuro.html
キーワード:直角三角形,正五角形
#Julia, #SymPy, #算額, #和算, #数学
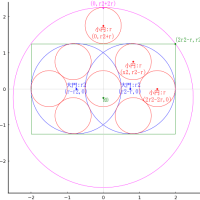
長方形の中に大小の正方形を容れ,長方形の一つの頂点と大小の正方形の頂点を結ぶ斜線を引く。長方形の長辺が 51 寸,小正方形の一辺の長さが 9 寸のとき,長方形の短辺の長さはいかほどか。
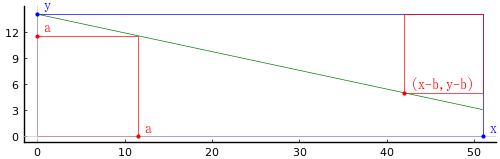
大正方形,小正方形の一辺の長さを a, b
長方形の長辺,短辺の長さを x, y
とおき,以下の方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms a::positive, b::positive, x::positive, y::positive
eq1 = b/(x - b) - (y - a)/a
ans_y = solve(eq1, y)[1]
ans_y |> println
a*x/(-b + x)
x = 51, b = 9 のとき,y = a*(17/14) である。
y, a の間には 17a = 14y の関係がある。
長方形の短辺の長さ y は,9 ≦ y ≦ 51 の範囲の任意の値を取れる。

しかし,問の最後に「乃各寸止」とある。整数解を求めよという意味であろう。
答は「横17寸」(現代で云う縦を横と称していた。横は長という)とある。
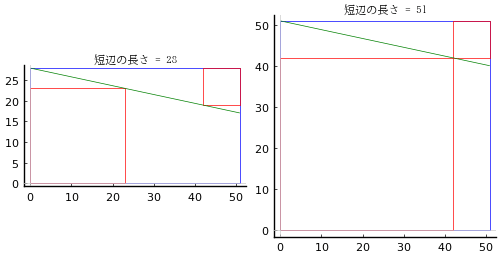
y, a の組としては,(17, 14) が最小解であるが,(34, 28), (51, 42) もありうる。
function draw(y, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x, b) = (51, 9)
a = y*(14/17)
p = plot([0, x, x, 0, 0], [0, 0, y, y, 0], color=:blue, lw=0.5)
rect(0, 0, a, a, :red)
rect(x - b, y - b, x, y, :red)
abline(0, y, -(y - a)/a, 0, x, :green)
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
if more
point(0, y, " y", :blue, :left, :bottom, delta=delta)
point(0, a, " a", :red, :left, :bottom, delta=delta)
point(x, 0, " x", :blue, :left, :bottom, delta=delta)
point(x - b, y - b, " (x-b,y-b)", :red, :left, :bottom, delta=delta)
point(a, 0, " a", :red, :left, :bottom, delta=delta)
ylims!(-3delta, y + 5delta)
end
if !more
point(51/2, y, @sprintf("短辺の長さ = %g", y), :black, :center, :bottom, delta=2delta, mark=false, fontsize=8)
end
return p
end;
draw(14, true)