算額（その1369）

算額（その1369）

五十九 群馬県佐波郡玉村町飯塚 光琳寺 天保8年(1837)
六十一 群馬県高崎市石原町 清水寺 天保10年(1839)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円22個，部分円（円欠），面積
#Julia, #SymPy, #算額, #和算

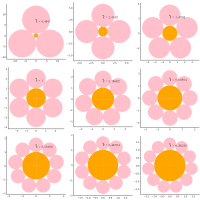
水平な弦で欠き取られた円の一部の中に等円を 22 個容れる。等円の直径が 1 寸のとき，黒積（図で黒塗りした面積の2倍）はいかほどか。

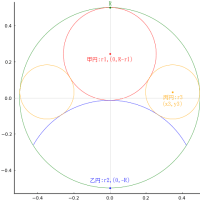
等円の半径を r，部分円の半径を R とする。

⊿ABC は一辺の長さが 8r，高さ（OD）が 2√3r の正三角形である。
A を中心として B, C を通る円（灰色で示す）は O を中心とする元の円と相似で，半径は AC = 8r である。
したがって，A, C は O を中心とする円の直径の上にある。

黒積は，半径 R の面積の 1/4 から，台形（OABD）の面積と等円の面積の (2 + 120/360 +  240/360) 倍を差し引いたものの 2 倍である。

等円の面積の 120/360 は A の等円から差し引くべき面積，240/360 は B の等円から差し引くべき面積である。

r = 1/2
R = 8r
S = 2*(pi*R^2/4 - (r + 5r)*4√3r/2 - pi*r^2*(2 + 120/360 +  240/360))

   10.028047402920391

黒積は 10.028047402920391 である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

function draw(r, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 8r
   plot()
   circlef(0, 0, R, :black, beginangle=0, endangle=180)
   circlef(0, 0, R, :white, beginangle=90, endangle=270)
   plot!([5r, r, -r, -5r, 5r], [0, 4√3r, 4√3r, 0, 0], seriestype=:shape, color=:white, lw=0.5)
   circle(0, 0, R, :blue)
   [circle2f(i*r, 0, r, :white) for i in (1,3,5,7)]
   [circle2f(i*r, 2√3r, r, :white) for i in (1,3)]
   circle2f(r, 4√3r, r, :white)
   [circle2f(i*r, √3r, r, :white) for i in (2, 4)]
   circle2f(2r, 3√3r, r, :white)
   circlef(0, 3√3r, r, :white)
   circlef(0, √3r, r, :white)

   [circle2(i*r, 0, r) for i in (1,3,5,7)]
   [circle2(i*r, 2√3r, r) for i in (1,3)]
   circle2(r, 4√3r, r)
   [circle2(i*r, √3r, r) for i in (2, 4)]
   circle2(2r, 3√3r, r)
   circle(0, 3√3r, r)
   circle(0, √3r, r)
   circle(5r, 0, R, :gray70)
   plot!([5r, r, 0, 0, 5r], [0, 4√3r, 4√3r, 0, 0], color=:green, lw=0.5)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, "R", :blue, :left, :bottom, delta=delta/2, deltax=delta/2)
       point(5r, 0, "A", :red, :center, delta=-delta/2)
       point(r, 4√3r, "B", :red, :center, :bottom, delta=delta/2)
       point(-3r, 0, "C", :red, :center, delta=-delta/2)
       point(0, 0, "O", :red, :left, delta=-delta/2, deltax=delta)
       point(0, 4√3r, "D", :red, :right, :bottom, delta=delta/2, deltax=-delta)
   end
end;

draw(1/2, true)