算額(その326)
早坂平四郎:算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
正方形に関するもの
千葉県成田市 成田不動新勝寺光明堂 明治30年(1897)
正方形内に半円 2 個,等円 3 個を図のように入れる。正方形の一辺の長さを等円の半径で表わせ。
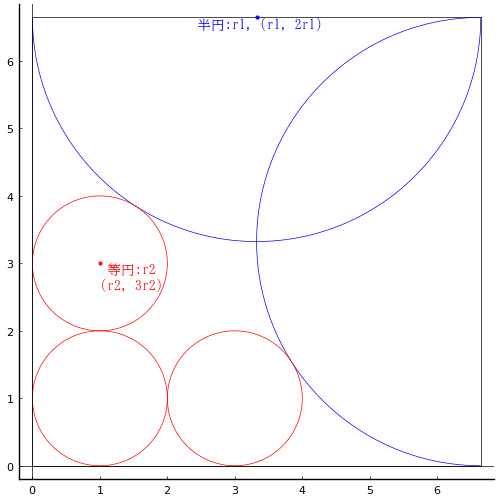
正方形の一辺の長さを 2r1 とする(半円の半径を r1 とする)。
等円の半径を r2 とする。
左上の半円と上の等円が接するという条件で,以下の方程式を解く。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::positive;
eq = (r1 - r2)^2 + (2r1 - 3r2)^2 - (r1 + r2)^2
solve(eq, r1) |> println
Sym[r2*(4 - sqrt(7))/2, r2*(sqrt(7) + 4)/2]
二通りの解が得られるが,r1 = r2*(sqrt(7) + 4)/2 が題意を満たす。
すなわち,正方形の一辺の長さ 2r1 は等円の半径の 4 + √7 倍である。
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r2 = 1
r1 = (4 + √7)/2
plot([0, 2r1, 2r1, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
circle(r1, 2r1, r1, :blue, beginangle=180, endangle=360)
circle(2r1, r1, r1, :blue, beginangle=90, endangle=270)
circle(r2, r2, r2)
circle(r2, 3r2, r2)
circle(3r2, r2, r2)
if more
point(r1, 2r1, " 半円:r1, (r1, 2r1)", :blue, :center)
point(r2, 3r2, " 等円:r2\n(r2, 3r2)", :red)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その325)
早坂平四郎:算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
正方形に関するもの
三重県津市大門町 慧日山観音寺 明治10年(1877)
正方形内に四分円 4 個,甲円 1 個,乙円 4 個,丙円 4 個を図のように入れる。丙円の直径を正方形の一辺の長さで表わせ。
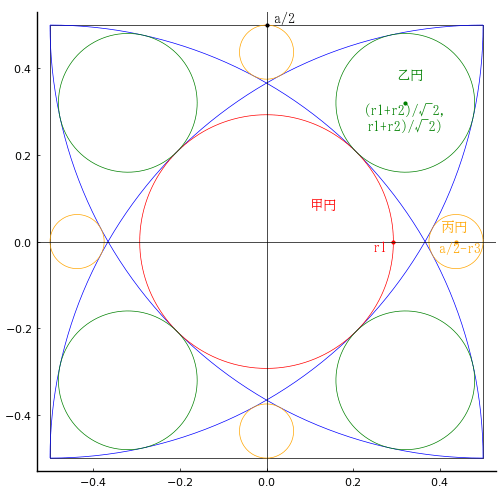
正方形の一辺の長さを a とする。
甲円の半径,中心座標を r1, (0, 0)
乙円の半径,中心座標を r2, ((r1+r2)/√2, (r1+r2)/√2)
丙円の半径,中心座標を r3, (a/2 - r3, 0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, r1::positive, r2::positive, r3::positive, x2::positive;
eq1 = 2(a/2)^2 - (a - r1)^2
eq2 = (a/2 + (r1 + r2)/sqrt(Sym(2)))^2 + (a/2 - (r1 + r2)/sqrt(Sym(2)))^2 - (a - r2)^2
eq3 = (a/2 - r3 + a/2)^2 + (a/2)^2 - (a + r3)^2
solve([eq1, eq2, eq3], (r1, r2, r3))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(-7*a*(-1/7 + 3*sqrt(2)/14)/3 + 2*a/3, a*(-1/7 + 3*sqrt(2)/14), a/16)
丙円の直径は a/8 すなわち正方形の一変の長さの 1/8 である。
甲円の半径は正方形の一変の長さの (2 - √2)/2 倍
-7*a*(-1//7 + 3*sqrt(Sym(2))/14)/3 + 2*a/3 |> simplify |> println
a*(2 - sqrt(2))/2
乙円の半径は正方形の一変の長さの (3√2 - 2)/14 倍
a*(-1//7 + 3*sqrt(Sym(2))/14) |> simplify |> println # r2
a*(-2 + 3*sqrt(2))/14
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = 1
(r1, r2, r3) = (a*(2 - √2)/2, a*(3√2 - 2)/14, a/16)
plot()
rect(-a/2, -a/2, a/2, a/2, :black)
circle(a/2, a/2, a, :blue, beginangle=180, endangle=270)
circle(-a/2, a/2, a, :blue, beginangle=270, endangle=360)
circle(-a/2, -a/2, a, :blue, beginangle=0, endangle=90)
circle(a/2, -a/2, a, :blue, beginangle=90, endangle=180)
circle(0, 0, r1)
circle4((r1 + r2)/√2, (r1 + r2)/√2, r2, :green)
circle42(0, a/2 - r3, r3, :orange)
if more
point(r1, 0, "r1 ", :red, :right)
point((r1 + r2)/√2, (r1 + r2)/√2, "(r1+r2)/√2,\nr1+r2)/√2)", :green, :center)
point(a/2 - r3, 0, " a/2-r3", :orange, :center)
point(0, a/2, " a/2", :black, :left, :bottom)
point(0.1a, 0.1a, "甲円", :red, mark=false)
point(0.3a, 0.4a, "乙円", :green, mark=false)
point(0.4a, 0.05a, "丙円", :orange, mark=false)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その324)
早坂平四郎:算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
四分円に関するもの
千葉県成田市 成田不動新勝寺光明堂 明治30年(1897)
元の算額では第一象限のみにいて書いているが,その限定は不要なので全体について述べる。
外円の中に,大円 4 個,中円 4 個,小円 4 個を入れる。図のように,中円は大円の交差する領域に,小円は 2 個の大円と外円に接する。小円の直径を中円の直径で表わせ。
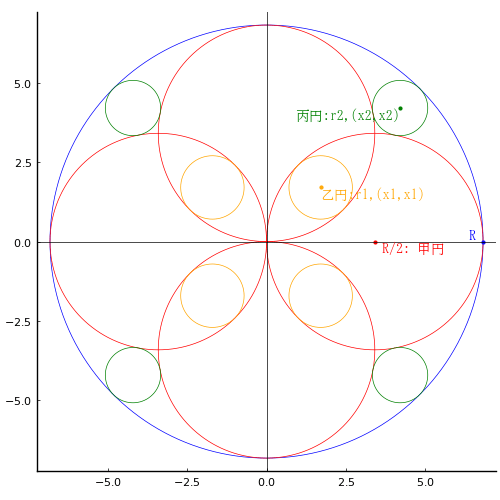
大円の半径,中心座標を R, (0, 0)
右側の大円の半径,中心座標を R/2, (R/2, 0)
第一象限にある中円の半径,中心座標を r1, (x1, x1), x1 = R/4
第一象限にある小円の半径,中心座標を r2, (x2, x2)
とし,r1 は未知数のまま,以下の連立方程式を r2, x2, R について解く。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, x1::positive, r2::positive, x2::positive;
r1 = 1
x1 = R/4
eq1 = (R/4)^2 + x1^2 - (R/2 - r1)^2
eq2 = 2x2^2 - (R - r2)^2
eq3 = (x2 - R/2)^2 + x2^2 - (R/2 + r2)^2
res = solve([eq1, eq2, eq3], (r2, x2, R));
res |> println
Tuple{Sym, Sym, Sym}[(2*r1*(-5*sqrt(2) - 4*sqrt(3 - 2*sqrt(2)) + 10)/17, 4*r1*(2 - sqrt(2))/17 + 24*r1*sqrt(3 - 2*sqrt(2))/17, 2*r1*(2 - sqrt(2))), (2*r1*(-5*sqrt(2) + 4*sqrt(3 - 2*sqrt(2)) + 10)/17, -24*r1*sqrt(3 - 2*sqrt(2))/17 + 4*r1*(2 - sqrt(2))/17, 2*r1*(2 - sqrt(2))), (2*r1*(5*sqrt(2) + 4*sqrt(2*sqrt(2) + 3) + 10)/17, -24*r1*sqrt(2*sqrt(2) + 3)/17 + 4*r1*(sqrt(2) + 2)/17, 2*r1*(sqrt(2) + 2)), (2*r1*(-4*sqrt(2*sqrt(2) + 3) + 5*sqrt(2) + 10)/17, 4*r1*(sqrt(2) + 2)/17 + 24*r1*sqrt(2*sqrt(2) + 3)/17, 2*r1*(sqrt(2) + 2))]
4 組目のものが適解である。
res[4]
(2*r1*(-4*sqrt(2*sqrt(2) + 3) + 5*sqrt(2) + 10)/17, 4*r1*(sqrt(2) + 2)/17 + 24*r1*sqrt(2*sqrt(2) + 3)/17, 2*r1*(sqrt(2) + 2))
それぞれを簡約化する。
res[4][1] |> sympy.sqrtdenest |> simplify |> println # r2
2*r1*(sqrt(2) + 6)/17
丙円の直径は乙円の直径の 2(√2 + 6)/17 倍である。
res[4][2] |> sympy.sqrtdenest |> simplify |> println # x2
4*r1*(8 + 7*sqrt(2))/17
res[4][3] |> simplify |> println # R
2*r1*(sqrt(2) + 2)
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 1
r2 = 2*r1*(sqrt(2) + 6)/17
x2 = 4*r1*(8 + 7*sqrt(2))/17
R = 2*r1*(sqrt(2) + 2)
x1 = R/4
plot()
circle(0, 0, R, :blue)
circle42(0, R/2, R/2)
circle4(x1, x1, r1, :orange)
circle4(x2, x2, r2, :green)
if more
point(R, 0, "R ", :blue, :right, :bottom)
point(R/2, 0, " R/2: 甲円", :red)
point(x1, x1, "乙円:r1,(x1,x1)", :orange)
point(x2, x2, "丙円:r2,(x2,x2)", :green, :right)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その323)
早坂平四郎:算額の一考察
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
長方形に関するもの
千葉県千葉市千葉寺 千葉寺 明治30年(1897)
外円内に長方形を入れ,対角線を引く。区切られた領域に 6 個の等円を入れる。外円の直径は等円の直径の何倍か。

外円の半径を R,等円の半径を r とおき,長方形内の等円の一個から対角線までの距離が等円の半径に等しいという方程式を解く。
include("julia-source.txt");
using SymPy
@syms R::positive, r::positive;
eq1 = distance(0, 0, R - 2r, sqrt(R^2 - (R - 2r)^2), R - 3r, r) - r^2;
res = solve(eq1, (R));
res |> println
Sym[2*r, 5*r, r*(5/2 - sqrt(5)/2)]
2 番目のものが適解。すなわち,外円の直径は等円の直径の 5 倍である。
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1
R = 5r
@printf("外円の径 = %.6f * 内円の径\n", R)
plot()
circle(0, 0, R, :blue)
circle(R - r, 0, r)
circle(r - R, 0, r)
circle4(R - 3r, r, r)
x = R - 2r
y = sqrt(R^2 - (R - 2r)^2)
rect(-x, -y, x, y, :green)
segment(-x, -y, x, y, :green)
segment(-x, y, x, -y, :green)
if more
point(R, 0, " R", :blue)
point(R - r, 0, " R-r", :red)
point(R - 2r, 0, " R-2r", :red)
point(R - 3r, r, "\n(R-3r,r)", :red, :center)
point(0, sqrt(R^2 - (R - 2r)^2), " √(R^2-(R-2r)^2)")
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その322)
早坂平四郎:算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
(16) 京都府京都市右京区山ノ内宮脇町 山王神社 明治23年(1890)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
直角三角形に関するもの
京都府京都市左京区西院 猿田彦神社 明治23年(1890)
鉤股弦内に正方形と正三角形を入れる。鈎が 3 寸,股が 7 寸のとき,三角形の一辺を求めよ。

正三角形と正方形の一辺の長さをそれぞれ a, b とする。
⊿OBE と ⊿OCF と ⊿ ODG は相似。
BE:BO = CF:CO = DG:DO = 3:7 なので以下の連立方程式を a, b について(鈎,股は未知数のままとして)解く。
include("julia-source.txt");
using SymPy
@syms 鈎::positive, 股::positive, 弦::positive, a::positive, b::positive, c::positive;
eq1 = sqrt(Sym(3))/2*a/(股 - b - a/2) - 鈎//股
eq2 = b/(股 - b) - 鈎//股
res = solve([eq1, eq2], (a, b));
res[a] |> factor |> println
res[b] |> println
2*股^2*鈎*(sqrt(3)*股 + 鈎)/((股 + 鈎)*(3*股^2 + 2*sqrt(3)*股*鈎 + 鈎^2))
股*鈎/(股 + 鈎)
a の分母にある 3*股^2 + 2*sqrt(3)*股*鈎 + 鈎^2 は (sqrt(3)*股 + 鈎)^2 で分子の (sqrt(3)*股 + 鈎) と約分され 2*股^2*鈎/((股 + 鈎)*(sqrt(3)*股 + 鈎)) になるが,SymPy ではそこまでの簡約化はできない。
鈎 = 3, 股 = 7 を代入すると,
正三角形の一辺 = 1.943884; 正方形の一辺 = 2.100000
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鈎, 股) = (3, 7)
a = 2*股^2*鈎/((股 + 鈎)*(sqrt(3)*股 + 鈎))
b = 股*鈎/(股 + 鈎)
@printf("正三角形の一辺 = %.6f; 正方形の一辺 = %.6f\n", a, b)
plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
rect(股 - b, 0, 股, b, :red)
plot!([股 - b - a, 股 - b - a/2, 股 - b], [0, √3a/2, 0, 0], color=:blue, lw=0.5)
if more
point(0, 0, "O ", :green, :right, :bottom)
point(股 - b - a, 0, "A ", :blue, :right, :bottom)
point(股 - b - a/2, 0, "B ", :blue, :right, :bottom)
point(股 - b, 0, " C", :red, :left, :bottom)
point(股, 0, "D ", :red, :right, :bottom)
point(股 - b - a/2, √3a/2, "E ", :blue, :right, :bottom)
point(股 - b, b, "F ", :red, :right, :bottom)
point(股, 鈎, "G ", :red, :right, :bottom)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その321)
長野県上田市別所温泉 北向観音堂 安永9年(1780)
中村信弥「改訂増補 長野県の算額」(32)
http://www.wasan.jp/zoho/zoho.html
大きな正方形の中に,甲, 乙, 丙, 丁 の正方形が入っている。
大きな正方形の一辺の長さが 10,甲,乙,丙,丁の面積の和が 30 歩,甲と乙の一辺の3乗和が 91,丙と丁の一辺の3乗和が 9 のとき,各正方形の一辺の長さを求めよ。
include("julia-source.txt");
using SymPy
@syms 甲::positive, 乙::positive, 丙::positive, 丁::positive;
eq1 = 甲^2 + 乙^2 + 丙^2 + 丁^2 - 30
eq2 = 甲^3 + 乙^3 - 91
eq3 = 丙^3 + 丁^3 - 9
eq4 = 甲 + 乙 + 丙 + 丁 - 10
solve([eq1, eq2, eq3, eq4], (甲, 乙, 丙, 丁))
4-element Vector{NTuple{4, Sym}}:
(3, 4, 1, 2)
(3, 4, 2, 1)
(4, 3, 1, 2)
(4, 3, 2, 1)
県内の算額(83)
長野県上田市別所温泉 北向観音堂 文化4年(1807) 前者との異同が不明。
同じ問題で数値の異なるもの。
@syms 単::positive, 複::positive, 奇::positive, 偶::positive;
eq1 = 単^2 + 複^2 + 奇^2 + 偶^2 - 30
eq2 = 単^3 + 複^3 - 72
eq3 = 奇^3 + 偶^3 - 28
eq4 = 単 + 複 + 奇 + 偶 - 10
solve([eq1, eq2, eq3, eq4], (単, 複, 奇, 偶))
4-element Vector{NTuple{4, Sym}}:
(2, 4, 1, 3)
(2, 4, 3, 1)
(4, 2, 1, 3)
(4, 2, 3, 1)

using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(単, 複, 奇, 偶) = (2, 4, 3, 1)
plot()
rect(0, 0, 10, 10, :black)
rect(0, 0, 偶, 偶, :blue)
rect(偶, 偶, 偶 + 奇, 偶 + 奇, :red)
rect(10 - 単 - 複, 10 - 単 - 複, 10 - 単, 10 - 単, :orange)
rect(10 - 単, 10 - 単, 10, 10, :magenta)
if more
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その320)
解析解は 算額(その834)を参照のこと
長野県長野市戸隠 戸隠山中院権現堂 安永5年(1776)
中村信弥「改訂増補 長野県の算額」(26)
http://www.wasan.jp/zoho/zoho.html
外円の中に中円1個,小円2個が入っている。外円の面積から中円・小円の面積を引くと 120 歩である。また,中円と小円の直径の差は 5 寸である。小円の直径を求めよ。

以下の連立方程式を解く。
eq4 の 3 は,この算額で用いる円周率の近似値である(120 はこれに依存している)。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, y::negative;
@syms R, r1, r2, y;
eq1 = r1 - r2 - 5//2
eq2 = r2^2 + (R - r1 - y)^2 - (r1 + r2)^2
eq3 = r2^2 + y^2 - (R - r2)^2
eq4 = 3*(R^2 - (r1^2 + 2r2^2)) - 120
# eq4 = r1 - 2r2
res = solve([eq1, eq2, eq3, eq4], (R, r1, r2, y))
2-element Vector{NTuple{4, Sym}}:
(-sqrt(185)/2, 5/2, 0, -sqrt(185)/2)
(sqrt(185)/2, 5/2, 0, sqrt(185)/2)
この連立方程式は正しいにも関わらず,小円の半径 = 0 という不適切な解を与える。
nlsolve() で数値解を求めると解が求まる。
println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
println(eq4, ", # eq4")
r1 - r2 - 5/2, # eq1
r2^2 - (r1 + r2)^2 + (R - r1 - y)^2, # eq2
r2^2 + y^2 - (R - r2)^2, # eq3
3*R^2 - 3*r1^2 - 6*r2^2 - 120, # eq4
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(R, r1, r2, y) = u
return [
2*r1 - 2*r2 - 5, # eq1
r2^2 - (r1 + r2)^2 + (R - r1 - y)^2, # eq2
r2^2 + y^2 - (R - r2)^2, # eq3
3*R^2 - 3*r1^2 - 6*r2^2 - 120, # eq4
]
end;
iniv = [big"10.0", 6, 4, -5]
res = nls(H, ini=iniv);
println(res);
(BigFloat[10.56270582162731798080457930499016663309319075011358623115618193017898504536659, 6.40671194097832904571536744155326822289140318621162475377480880617077430209802, 3.90671194097832904571536744155326822289140318621162475377480880881194616675602, -5.388864105677014011100110408852971086316399261553975564921545695903341835297999], true)
R = 10.562706; r1 = 6.406712; r2 = 3.906712; y = -5.388864
小円の直径 = 7.813423881956658
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r1, r2, y) = res[1]
@printf("R = %.6f; r1 = %.6f; r2 = %.6f; y = %.6f\n", R, r1, r2, y)
println("小円の直径 = $(Float64(2r2))")
plot()
circle(0, 0, R, :black)
circle(0, R - r1, r1)
circle(r2, y, r2, :blue)
circle(-r2, y, r2, :blue)
if more
point(0, R - r1, " R-r1")
point(R, 0, " R")
point(r2, y, "(r2,y)")
annotate!(0.8, -4, text("小円の直径 = " * @sprintf("%.5f", 2r2), :left, 9))
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その319)
長野県長野市戸隠 戸隠山中院権現堂 安永5年(1776)
中村信弥「改訂増補 長野県の算額」(27)
http://www.wasan.jp/zoho/zoho.html
鈎股内に中鈎を引き,区切られた領域に中円,小円を入れる。中円の直径と弦の和が 48 寸,股と小円の直径の和が 52 寸であるとき,中鈎はいかほどか。

以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms 鈎::positive, 股::positive, 弦::positive, 中鈎::positive,
長弦::positive, 短弦::positive, 中円径::positive, 小円径::positive,
x::positive, y::positive;
eq1 = 中円径 + 長弦 - 48
eq2 = 股 + 小円径 - 52
eq3 = 鈎*股/2 - 中鈎*弦/2
eq4 = (長弦 + 股 + 中鈎)*中円径/4 + (鈎 + 短弦 + 中鈎)*小円径/4 - 中鈎*弦/2
eq5 = 短弦^2 + 中鈎^2 - 鈎^2
eq6 = 中鈎^2 + 長弦^2 - 股^2
eq7 = 長弦 + 中鈎 - 股 - 中円径
eq8 = 短弦 + 中鈎 - 鈎 - 小円径
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (鈎, 股, 弦, 中鈎, 長弦, 短弦, 中円径, 小円径))
1-element Vector{NTuple{8, Sym}}:
(30, 40, 50, 24, 32, 18, 16, 12)
中鈎は 24 寸
図を描くためには中円,小円の中心座標が必要であるが,上の連立方程式とまとめて解こうとすると solve() では無理である。そこで,上で得られた値に基づいて連立方程式を解く。
using SymPy
@syms 鈎::positive, 股::positive, 弦::positive, 中鈎::positive,
長弦::positive, 短弦::positive, 中円径::positive, 小円径::positive,
x::positive, # 中円の中心の x 座標
y::positive; # 小円の中心の y 座標
(鈎, 股, 弦, 中鈎, 長弦, 短弦, 中円径, 小円径) = (30, 40, 50, 24, 32, 18, 16, 12)
eq9 = distance(0, 鈎, 股, 0, x, 中円径//2) - (中円径//2)^2
eq10 = distance(0, 鈎, 股, 0, 小円径//2, y) - (小円径//2)^2
res2 = solve([eq9, eq10], (x, y))
4-element Vector{Tuple{Sym, Sym}}:
(16, 18)
(16, 33)
(128/3, 18)
(128/3, 33)
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鈎, 股, 弦, 中鈎, 長弦, 短弦, 中円径, 小円径) = (30, 40, 50, 24, 32, 18, 16, 12)
(x, y) = (16, 18)
@printf("中円の直径 = %.6f\n", 中円径)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
circle(x, 中円径/2, 中円径/2)
circle(小円径/2, y, 小円径/2, :blue)
(x1, y1) = (中鈎*3/5, 中鈎*4/5)
segment(0, 0, x1, y1)
if more
point(0, 0, " O", :green, :left, :bottom)
point(股, 0, " A", :green, :left, :bottom)
point(0, 鈎, " B", :green, :left, :bottom)
point(x1, y1, " C", :green, :left, :bottom)
annotate!(15, 25, text("鈎:OB, 股:OA, 弦:AB, 中鈎:OC\n長弦:AC, 短弦:BC", 10, :left))
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その318)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額(75)
長野県長野市元善町 善光寺 文化元年(1804)
正八角形の対角線で区切られた三角形に内接する円の直径を求めよ。

問では,間に一つの頂点を挟んだ2つの頂点間の対角線の長さ(距斜)と正八角形の一辺(濶)を与えたときの各円の直径を求めよと書かれているが,この 2 つの量はいずれも外円の半径により求められるので,外円の半径 R を適当に定めれば各円の直径を求めることができる。ここでは,R = 1 とする。
外円の半径と中心座標 R, (0, 0)
甲円の半径と中心座標 r1, (R/√2 + r1, 0)
乙円の半径と中心座標 r2, (R/√2 - r2, y2)
丙円の半径と中心座標 r3, (x3, y3)
丁円の半径と中心座標 r3, (-y3, -x3)
戊円の半径と中心座標 r2, (-y2, -R/√2 + r2)
以下の連立方程式を解く。3 組の連立方程式 [eq1], [eq2, eq3], [eq4, eq5, eq6] は互いに独立。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive;
@syms a, b
R = 1
a = R/sqrt(Sym(2))
b = sqrt((R - R/sqrt(Sym(2)))^2 + (R/sqrt(Sym(2)))^2)
eq1 = distance(R/sqrt(Sym(2)), R/sqrt(Sym(2)), R, 0, R/sqrt(Sym(2)) + r1, 0) - r1^2
res1 = solve(eq1, r1)[1]
res1 |> println
(-sqrt(2 - sqrt(2)) + sqrt(2)*(2 - sqrt(2)))/(2 - sqrt(2))^(3/2)
@syms r2::positive, y2::positive;
eq2 = distance(0, R, R/sqrt(Sym(2)), R/sqrt(Sym(2)), R/sqrt(Sym(2)) - r2, y2) - r2^2
eq3 = distance(0, R, R/sqrt(Sym(2)), -R/sqrt(Sym(2)), R/sqrt(Sym(2)) - r2, y2) - r2^2
res2 = solve([eq2, eq3], (r2, y2))
2-element Vector{Tuple{Sym, Sym}}:
(sqrt(2)*(-sqrt(2)/2 - (1 - sqrt(2)/2)^(3/2) + 1/2 + sqrt(1 - sqrt(2)/2)), sqrt(1 - sqrt(2)/2))
(sqrt(2)*(-(sqrt(2)/2 + 1)^(3/2) + 1/2 + sqrt(2)/2 + sqrt(sqrt(2)/2 + 1)), sqrt(sqrt(2)/2 + 1))
最初の解が適解である。
@syms r3::positive, x3::negative, y3::positive;
eq4 = distance(0, R, R/sqrt(Sym(2)), -R/sqrt(Sym(2)), x3, y3) - r3^2
eq5 = distance(0, R, -R/sqrt(Sym(2)), R/sqrt(Sym(2)), x3, y3) - r3^2
eq6 = distance(R/sqrt(Sym(2)), -R/sqrt(Sym(2)), -R/sqrt(Sym(2)), R/sqrt(Sym(2)), x3, y3) - r3^2
res3 = solve([eq4, eq5, eq6], (r3, x3, y3))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(sqrt(-sqrt(4 - 2*sqrt(2)) - sqrt(2)/2 + 2), sqrt(2)*(-sqrt(2)*sqrt(2 - sqrt(2)) - sqrt(2 - sqrt(2)) + 1)/2, sqrt(1 - sqrt(2)/2) + sqrt(2)/2)
(sqrt(-sqrt(2*sqrt(2) + 4) + sqrt(2)/2 + 2), sqrt(2)*(-sqrt(sqrt(2) + 2) - 1 + sqrt(2)*sqrt(sqrt(2) + 2))/2, -sqrt(2)/2 + sqrt(sqrt(2)/2 + 1))
2番めの解が適解である。
甲円の直径 = 0.281305
乙円(戊円)の直径 = 0.496606
丙円(丁円)の直径 = 0.613126
# 正八角形の頂点座標
R = 1
x = zeros(9)
y = zeros(9)
for i in 1:8
θ = (i - 1)*pi/4
x[i] = cos(θ)R
y[i] = sin(θ)R
end
x[9] = x[1]
y[9] = y[1]
function symmetry(x, y, r, color=:red)
circle(x, y, r, color)
circle(-y, -x, r, color)
end;
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = (-sqrt(2 - sqrt(2)) + sqrt(2)*(2 - sqrt(2)))/(2 - sqrt(2))^(3/2)
(r2, y2) = (sqrt(2)*(-sqrt(2)/2 - (1 - sqrt(2)/2)^(3/2) + 1/2 + sqrt(1 - sqrt(2)/2)), sqrt(1 - sqrt(2)/2))
(r3, x3, y3) = (sqrt(-sqrt(2*sqrt(2) + 4) + sqrt(2)/2 + 2), sqrt(2)*(-sqrt(sqrt(2) + 2) - 1 + sqrt(2)*sqrt(sqrt(2) + 2))/2, -sqrt(2)/2 + sqrt(sqrt(2)/2 + 1))
@printf("甲円の直径 = %.6f\n乙円(戊円)の直径 = %.6f\n丙円(丁円)の直径 = %.6f\n", 2r1, 2r2, 2r3)
plot(x, y, color=:black, lw=0.5)
circle(0, 0, R)
symmetry(R/√2 + r1, 0, r1, :green)
symmetry(R/√2 - r2, y2, r2, :orange)
symmetry(x3, y3, r3, :magenta)
for i in 2:6
segment(x[i], y[i], x[8], y[8], :blue)
end
if more
point(R/√2 + r1, 0, "甲:r1\n(R/√2,0)", :green, :center, :bottom)
point(R/√2 - r2, y2, "乙:r2\n(R/√2-r2,y2)\n", :orange, :center, :bottom)
point(x3, y3, "丙:r3\n(x3,y3)\n", :magenta, :center, :bottom)
point(-y3, -x3, " 丁", :magenta)
point(-y2, -R/√2 + r2, " 戊", :orange)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その317)
p02-03 特集「算額」(杉浦).indd
https://www.s-coop.net/lifestage/backnumber/2011/pdf/1106_02-03.pdf
御香宮の算額
甲,乙,丙の 3 つの正方形は,以下の条件を満たす。
1. 各面積の和はある一定の値を取る
2. 甲の一辺の 3 乗根,乙の一辺の 5 乗根,丙の一辺の 7 乗根の和はある一定の値を取る
3. 甲と乙の一辺の長さの差と,乙と丙の一辺の長さの差は等しい
このとき,甲,乙,丙それぞれの辺の長さを求めよ。
御香宮神社の算額
http://tadahikostar.blog21.fc2.com/blog-entry-3847.html
には,鮮明な写真が掲載されている。

読んだところでは,
1. 甲乙丙の各平積の和が既知,
2. 甲の開立方,乙の開四乗方,丙の開六乗方の和が既知
3. 甲,乙,丙の一辺の長さは等差数列(甲>乙>丙)
で,条件 2. が違う。
また,
御香宮(京都・伏見)の算額の問題 - 高精度計算サイト - Keisan
https://keisan.casio.jp/exec/user/1465639202
では,
2. 甲の1辺の3乗と乙の1辺の5乗と丙の1辺の7乗がある値をとり
と書かれている。これは明らかに誤りである。
「開立」は立方根を表す。三乗は「再自乗」という。
以下では,「甲の開立方,乙の開四乗方,丙の開六乗方の和」を採用する。
既知である値を記号(変数)として解くのは solve() でも無理である。
また,既知の値を具体的に与えても solve() では解けないので,nlsolve() で数値解を求める。
具体的に,既知の値を求めておく。甲,乙,丙の辺の長さをそれぞれ 6, 4, 2 として,条件 1, 2 で表される数値を計算する。
(甲, 乙, 丙) = (6, 4, 2)
甲^2 + 乙^2 + 丙^2 |> println # a とする
甲^(1/3) + 乙^(1/4) + 丙^(1/6) |> println # b とする
56
4.353796203514608
丙^2 + 乙^2 + 甲^2 - 56, # eq1
丙^0.166666666666667 + 乙^0.25 + 甲^0.333333333333333 - 4.35379620351461, # eq2
丙 - 2*乙 + 甲, # eq3
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(甲, 乙, 丙) = u
return [
丙^2 + 乙^2 + 甲^2 - 56, # eq1
丙^0.166666666666667 + 乙^0.25 + 甲^0.333333333333333 - 4.35379620351461, # eq2
丙 - 2*乙 + 甲, # eq3
]
end;
初期値により,二通りの解が示される。両方ともに,条件を満たしている。
iniv = [big"7.0", 4.1, 1.1]
res = nls(H, ini=iniv);
println(res);
(BigFloat[5.999999999999978421814505360998991236330686683731818877458530801081713663484236, 4.000000000000010789092747335389143058164701865210416514719281049866373768067708, 2.000000000000043156370989309779294879998717046689014151980031298601986612507766], true)
(甲, 乙, 丙) = res[1] # 6, 4, 2
丙^2 + 乙^2 + 甲^2 - 56, # eq1
丙^0.166666666666667 + 乙^0.25 + 甲^0.333333333333333 - 4.35379620351461, # eq2
丙 - 2*乙 + 甲 # eq3
(2.566627137897993161354744300647618625279842621939623293996006529315262445625456e-25, -3.867992033135278266328028707026632666657885527869404966426262217141461630526278e-27, -4.904726014337897321140092172924707876804539997277609351100695166069929253914544e-65)
iniv = [big"3.0", 2.1, 1.2]
res = nls(H, ini=iniv);
println(res);
(BigFloat[4.417532066579428278706241618180857546089192311716748510275041555425975958939494, 4.319756156028245623996284797567623698490811039184724945910874439881535311042085, 4.221980245477062969286327976954389850892429766652701381546707324388269228906724], true)
(甲, 乙, 丙) = res[1] # 4.417532066579429, 4.319756156028245, 4.221980245477063
丙^2 + 乙^2 + 甲^2 - 56, # eq1
丙^0.166666666666667 + 乙^0.25 + 甲^0.333333333333333 - 4.35379620351461, # eq2
丙 - 2*乙 + 甲 # eq3
(7.928474500472361481718927810447226817906506437873289558404530451020621884955364e-25, -5.071109598580144750966960369570845052151000656128305908528664840899463931562674e-27, 5.117456576204827560281226639245275222567489206961363157351246079614929159341669e-65)
算額(その316)
(4) 京都府長岡京市天神 長岡天満宮 寛政2年(1970)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
森田健(2020): 日本文化としての数学:和算と算額, 日本語・日本文化,2020,47,p81-107.
https://ir.library.osaka-u.ac.jp/repo/ouka/all/75881/JLC_47_081.pdf
p02-03 特集「算額」(杉浦).indd
https://www.s-coop.net/lifestage/backnumber/2011/pdf/1106_02-03.pdf
キーワード:円2個,正三角形,直線上
大円と小円の間に正三角形が挟まっている。大円と小円の直径はそれぞれ 18cm,8cm である。正三角形の辺の長さを求めよ。
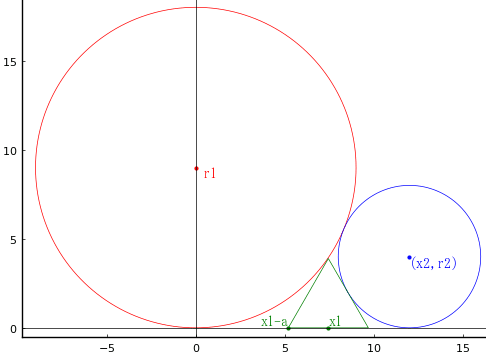
大円の半径を r1,中心座標を (0, r1)
小円の半径を r2,中心座標を (x2, r2)
正三角形の一辺の長さを 2a,底辺の中点の x 座標を x1 とする。
以下の連立方程式を解く。
なお,eq1 は直線の上にある外接する 2 つの円の中心間の距離を表すもので,距離 = x2 = 2sqrt(r1, r2) である。eq2, eq3 はそれれぞれの円の中心から正三角形の斜辺までの距離についての方程式である。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::positive, x2::positive, x1::positive, a::positive;
(r1, r2) = (9, 4)
eq1 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = distance(x1 - a, 0, x1, sqrt(Sym(3))a, 0, r1) - r1^2
eq3 = distance(x1 + a, 0, x1, sqrt(Sym(3))a, x2, r2) - r2^2;
res = solve([eq1, eq2, eq3], (x1, a, x2))
3-element Vector{Tuple{Sym, Sym, Sym}}:
(6 - 5*sqrt(3)/2, 6 + 13*sqrt(3)/2, 12)
(6 + 7*sqrt(3)/2, sqrt(3)/2 + 6, 12)
(5*sqrt(3)/6 + 6, 6 - 13*sqrt(3)/6, 12)
三番目の組が適解である。
(5*sqrt(3)/6 + 6, 6 - 13*sqrt(3)/6, 12)
(7.4433756729740645, 2.247223250267433, 12)
正三角形の一辺の長さ = 4.494446500534866 cm
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (9, 4)
x1 = 5*sqrt(3)/6 + 6
a = 6 - 13*sqrt(3)/6
x2 = 12
println("正三角形の一辺の長さ = $(2a) cm")
plot()
circle(0, r1, r1)
circle(x2, r2, r2, :blue)
plot!([x1 - a, x1 + a, x1, x1 - a], [0, 0, √3a, 0], color=:green, lw=0.5)
if more
point(0, r1, " r1", :red)
point(x2, r2, "(x2,r2)", :blue)
point(x1, 0, "x1", :green, :left, :bottom)
point(x1 - a, 0, "x1-a", :green, :right, :bottom)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
算額(その315)
(5) 京都府宮津市天橋立文殊 知恩寺文殊堂 文政元年(1818)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
p02-03 特集「算額」(杉浦).indd
https://www.s-coop.net/lifestage/backnumber/2011/pdf/1106_02-03.pdf
小円の直径を 8 cm,大円の直径を 16 cm とする。色をつけた部分の面積を求めよ。

似た図形を取り上げた算額は,京都府宮津市天橋立の知恩寺文殊堂に文政元年(1818)に奉納されたものがある(算額その28)。それは大円と小円の径を求めよというものである。
図形は点対称・線対称なので,角度 30° から 90°までの該当図形の面積を求めて 6 倍すればよい。
図中の下の灰色の三日月様の面積は,その上のピンクの領域の面積と同じである。求める灰色の領域の面積は大円の面積の 1/3 から小円の面積の 1/2 を引いたものである。

求める面積は 251.32741228718342 平方センチメートル
(r1, r2) = (8, 4)
pi*(r1^2/3 - r2^2/2) * 6
251.32741228718342
include("julia-source.txt");
function transform(x, y; deg=0, dx=0, dy=0)
(x, y) = [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * [x, y]
return (x .+ dx, y .+ dy)
end;
function arc(r; beginangle=0, endangle=360)
n = round(Int, abs(endangle - beginangle)r/4)
x = []
y = []
for θ in range(beginangle, endangle, length=n)
append!(x, cosd(θ))
append!(y, sind(θ))
end
#append!(x, x[1])
#append!(y, y[1])
return (r .* x, r .* y)
end;
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (8, 4)
plot()
if more
circle(0, 0, r1)
rotate(0, r1, r1)
rotate(0, r1 + r2, r2)
(x1, y1) = arc(r1, beginangle=90, endangle=-30)
(x1, y1) = transform(x1, y1, dy=r1)
(x2, y2) = arc(r2, beginangle=-90, endangle=90)
(x2, y2) = transform(x2, y2, dy=r1+r2)
(x3, y3) = arc(r1, beginangle=30, endangle=90)
plot!([x3; x2; x1], [y3; y2; y1], linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
(x4, y4) = arc(r1, beginangle=30, endangle=90)
append!(x4, x4[1])
append!(y4, y4[1])
plot!(x4, y4, linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:pink)
(x5, y5) = transform(x4, y4, deg=60, dx=r1√3/2, dy=-r1/2)
plot!(x5, y5, linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
rotatef(0, r1, r1, :gray)
rotatef(0, r1 + r2, r2, :white)
circlef(0, 0, r1, :white)
rotate(0, r1, r1, :red)
rotate(0, r1 + r2, r2, :red)
circle(0, 0, r1, :red)
(x4, y4) = arc(r1, beginangle=30, endangle=90)
(x5, y5) = transform(x4, y4, deg=60, dx=r1√3/2, dy=-r1/2)
(x6, y6) = transform(x4, y4, deg=-120, dy=r1)
x7 = [x5; x6]
y7 = [y5; y6]
plot!(x7, y7, linecolor=:red, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
(x8, y8) = transform(x7, y7, deg=120)
plot!(x8, y8, linecolor=:red, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
(x9, y9) = transform(x7, y7, deg=240)
plot!(x9, y9, linecolor=:red, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
plot!(showaxis=false)
end
end;
某氏のプログラムで(プログラミング言語は何だっていい,言わんとしていることはわかるだろう)
switch mat_ver
case 1
mat_name='R2019a';
case 2
mat_name='R2007b';
case 3
mat_name='ver7.1';
case 4
mat_name='ver5.3';
end
というような類似部分が,何箇所もある。簡明直截ではあるが,ダサい。
name = ['R2019a', 'R2007b', 'ver7.1', 'ver5.3']
mat_name = name[mat_ver]
でいいじゃないか。
更には,中間変数なんぞも不要で,
mat_name = ['R2019a', 'R2007b', 'ver7.1', 'ver5.3'][mat_ver]
のほうが,どれだけわかりやすいか。
こういうプログラムを書く人は信用ならん。
資格確認書をプッシュ型で届けると言っているけど,従来の保険証を自治体から送っていたのとどこが違うのか?マイナ保険証を使っていない人を特定してから,その人あてに資格確認証を送るの?なんかひと手間かかるようで,またそこで齟齬が発生する可能性が出るのでは?
今まで通り,自治体から保険証を送るので,なんの問題もないのでは?
バカ麻生も,「マイナンバーカードなんてなんのメリットもない,わしは使ったことない」といってるぞ。
そういうことをやってくれるなら(手間だの,費用だのは政府が持つということなら),マイナカード返上してしまおうかな。だって,マイナカード持っていなくても,今まで通りやってもらえるのなら,マイナカード持つ必要性ない(ちなみに,私は申請時期が遅かったので,マイナポイントはもらっていない。なんのメリットも受けていないので,マイナカード返上しても,「マイナポイントただ取り」などと言われる筋合いはない)。
もっとも,ばかな政府のばかな施策を利用した一般国民を「マイナポイントただ取り」呼ばわりするのは門違いなのだが。




















