算額（その1562）

算額（その1562）

七十一 岩手県一関市川崎町薄衣諏訪前 浪分神社 明治35年(1902)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：球4個，円錐1個，四角柱1個
#Julia, #SymPy, #算額, #和算

底面が正方形の四角柱の中に等球 4 個と円錐 1 個を容れる。円錐と四角柱の高さは等しい。等球は 2 個の等球と外接し，円錐と 1 点で外接し，四角柱に 3 点で内接する。等球の直径が与えられたとき，円錐（四角柱）の高さはいかほどか。

円錐の底面の半径と中心座標を a, (0, 0, 0)
四角柱の底面の座標を (a, a, 0), (a, -a, 0), (-a, a, 0), (-a, -a, 0)
等球の半径と中心座標を r, (a - r, a - r, h - r); a = 2r
とおき，以下の連立方程式を解く。

include("julia-source.txt")
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
using LinearAlgebra

function shortest_distance_to_line(p0, p1, p2)
    """
    点 p0 から p1, p2 を通る直線までの垂直距離を計算
    """
    line_dir = p2 - p1　　# 直線の方向ベクトル
    numerator = norm(cross(line_dir, p0 - p1))  # 外積の大きさ
    denominator = norm(line_dir)  # 直線の方向ベクトルの大きさ
    return numerator / denominator
end;

@syms a::positive, h::positive, r::positive
a = 2r
eq = shortest_distance_to_line([a - r, a - r, h - r], [a/√Sym(2), a/√Sym(2), 0], [0, 0, h]) - r
eq |> println

    -r + sqrt(2)*Abs(h*(-sqrt(2)*r + r) + sqrt(2)*r*(h - r))/sqrt(h^2 + 4*r^2)

ans_h = solve(eq, h)[1]
ans_h |> println

    4*sqrt(2)*r

円錐の高さ h は，等円の半径 r の 4√2 倍である。
等円の直径が 1 寸のとき，円錐の高さは 2√2 = 2.82842712474619 寸である。

算額（その1561）

算額（その1561）

六十五 岩手県花泉町金沢 大門神社・大門観世音菩薩 明治33年(1900)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，外円，二等辺三角形
#Julia, #SymPy, #算額, #和算

甲円と交差する二等辺三角形を設け，隙間に乙円 3 個を容れる。乙円の直径が与えられたとき，甲円の直径はいかほどか。

甲円の半径と中心座標を R, (0, 0)
乙円の半径と中心座標を r, (0, -R - r), (x, y)
二等辺三角形の底辺の端点の座標を (-R - 2r, a)
とおき，以下の連立方程式を解く。

include("julia-source.txt")
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, r, x, y, a
eq1 = r/(2R + r) - a/sqrt((2R + 2r)^2 + a^2)
eq2 = dist2(0, R, a, -R - 2r, x, y, r)
eq3 = x^2 + y^2 - (R - r)^2
eq4 = y/x - a/(2R + 2r);

一度に解けないので，eq1, eq3, eq4 から a, x, y を求める。

res = solve([eq1, eq3, eq4], (a, x, y))[2]  # 2 of 4

    (r*sqrt(R*(R^3 - R^2*r - R*r^2 + r^3)/(4*R^2 + 4*R*r + r^2))*(-2*R - r)/(R*(-R + r)), 2*sqrt(R*(R^3 - R^2*r - R*r^2 + r^3)/(4*R^2 + 4*R*r + r^2)), r*(R - r)/(2*R + r))

eq2 に代入し，eq12 式を求める。

eq12 = eq2(a => res[1], x => res[2], y => res[3]) |> simplify
eq12 |> println

    4*R*(R^3 - R^2*r - 3*R*r^2 - r^3)

eq12 を解いて R を求める。

ans_R = solve(eq12, R)[4]  # 4 of 4
ans_R |> println

    r*(1 + sqrt(2))

甲円の直径は，乙円の直径の (1 + √2) 倍である。

乙円の半径が 1 のとき，全てのパラメータは以下のとおりである。
r = 1;  R = 2.41421;  a = 1.18921;  x = 1.39324;  y = 0.242641

function draw(r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    R = r*(1 + √2)
    (a, x, y) = (r*sqrt(R*(R^3 - R^2*r - R*r^2 + r^3)/(4R^2 + 4R*r + r^2))*(-2R - r)/(R*(-R + r)), 2sqrt(R*(R^3 - R^2*r - R*r^2 + r^3)/(4R^2 + 4R*r + r^2)), r*(R - r)/(2R + r))
    @printf("r = %g;  R = %g;  a = %g;  x = %g;  y = %g\n", r, R, a, x, y)
    plot([a, -a, 0, a], [-R - 2r, -R - 2r, R, -R - 2r], color=:red, lw=0.5)
    circle(0, 0, R, :green)
    circle2(x, y, r, :blue)
    circle(0, -R - r, r, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, R, "R", :green, :center, :bottom, delta=delta/2)
        point(0, -R, "-R", :green, :center, :bottom, delta=delta/2)
        point(x, y, "乙円:r,(x,y)", :blue, :center, delta=-delta/2)
        point(0, -R - r, "乙円:r,(0,-R-r)", :blue, :center, delta=-delta/2)
    end
end;

draw(1, true)

算額（その1560）

算額（その1560）

六十一 岩手県花泉町金沢 大門神社・大門観世音菩薩 慶応元年(1865)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図 03051
https://w.atwiki.jp/sangaku/pages/290.html

キーワード：球4個，3次元
#Julia, #SymPy, #算額, #和算

台の上に甲球 1 個，乙球 2 個，丙球 1 個が載っている。甲球，乙球の直径が 180 寸，72寸，及び「高さ」が 144 寸のとき，丙球の直径はいかほどか。

山村は，問に「甲球一ケ乙球二個載丙球一ケ」と書かれているのに，「乙球 1 個，丙球 2 個」を描くという凡ミスを犯している。術を解説しているがオウム返しであり，乙球と丙球の大きさの逆転にも気づいていない。

これは，「算額（その1515）」の「八十三 保呂羽神社」の算額で，「乙球の直径及び「高」が与えられたとき」であるものが，それぞれの数値が具体的に与えられているだけである。

算額（その1515）の一般解に，数値を代入するだけでよい。

res[1](r1 => 180/2, r2 => 72/2, h => 144).evalf() |> println
res[2](r1 => 180/2, r2 => 72/2, h => 144) |> println
res[3](r1 => 180/2, r2 => 72/2, h => 144) |> println
res[4](r1 => 180/2, r2 => 72/2, h => 144).evalf() |> println

    42.5000000000000
    108.000000000000
    132.000000000000
    101.500000000000

丙球の直径は 2 * 42.5 = 85 寸である。

本格手打 もり屋 高松本店

高松市香川町川内原 本格手打 もり屋 高松本店
一番のおすすめは写真の右の大看板にもある「かき揚げおろしうどん ¥980.」
座敷席からは，もりの大将がうどん打ち・手切りしているところを見ることができるかも

算額（その1559）

算額（その1559）

五十一 岩手県一関市西風 西風白山神社 明治18年(1885)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図
https://w.atwiki.jp/sangaku/pages/311.html

キーワード：円9個，外円，円弧2個
#Julia, #SymPy, #算額, #和算, #数学

外円の中に円弧 2 個，大円 2 個，小円 6 個を容れる。外円の直径が与えられたとき，小円の直径を求めよ。

山村の図には，円弧 2 個がない。山村は，「問」にある二文字を読み飛ばしている。
『今有如図外円径内隔孤容大円径二個小円径六個其外円若干小円径幾何ナルヤ』
外円径内隔孤容，すなわち，外円の中に弧で隔てて◯◯を容れる。
「今有如図」には円弧が描かれている。
この円弧がないと「術」と合わない解（汚い解）しか得られない。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1); r1 = R/2
小円の半径と中心座標を r2, (R - r1, 0), (x2, y2)
円弧の半径と中心座標を r0, (0, r0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r0::positive, r1::positive,
      r2::positive, x2::positive, y2::positive,
      x0::positive, y0::positive;
r1 = R/2
eq1 = x2^2 + (r1 - y2)^2 - (r1 + r2)^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = x2^2 + (r0 - y2)^2 - (r0 - r2)^2
eq4 = (R - r2)^2 + r0^2 - (r0 + r2)^2
eq5 = x0^2 + y0^2 - R^2
eq6 = x0^2 + (r0 - y0)^2 - r0^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (r2, x2, y2, r0, x0, y0))[1]

    (R/5, 2*sqrt(3)*R/5, 2*R/5, 3*R/2, 2*sqrt(2)*R/3, R/3)

小円の半径 r2 は，外円の半径 R の 1/5 である。
すなわち，外円の直径が 5 寸のとき，小円の直径は 1 寸である。

ちなみに，山村の解釈のように円弧がない場合には，小円同士が外接するようになり，外円の直径が 5 寸のとき，小円の直径は  1.01331 のように半端な数値になり，「算額の対象にするにはみっともない」ことになってしまう。

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r1 = R/2
    (r2, x2, y2, r0, x0, y0) = (R/5, 2*sqrt(3)*R/5, 2*R/5, 3*R/2, 2*sqrt(2)*R/3, R/3)
    @printf("外円の直径が %g のとき，小円の直径は %g である。\n", 2R, 2r2)
    θ = atand(y0 - r0, x0)
    plot()
    circle(0, r0, r0, :black, beginangle=180 - θ, endangle=360 + θ, n=1000)
    circle(0, -r0, r0, :black, beginangle=- θ, endangle=180 + θ, n=1000)
    circle(0, 0, R, :green)
    circle22(0, r1, r1)
    circle4(x2, y2, r2, :blue)
    circle2(R - r2, 0, r2, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end  
end;

draw(5, true)

算額（その1558）

算額（その1558）

五十 岩手県一関市西風 西風白山神社 弘化2年(1845)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，等脚台形，対角線
#Julia, #SymPy, #算額, #和算, #数学

等脚台形の中に対角線を引き，大円，甲円，乙円を容れる。甲円，乙円の直径が与えられたとき，大円の直径はいかほどか。

上底，下底を 2b, 2a とおく。高さは 2r1 である。
大円の半径と中心座標を r1, (0, r1)
甲円の半径と中心座標を r2, (x2, r2)
乙円の半径と中心座標を r3, (x3, 2r1 - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, r1::positive,
      r2::positive, x2::positive,
      r3::positive, x3::positive;
eq1 = dist(a, 0, b, 2r1, 0, r1) - r1^2
eq2 = dist(a, 0, b, 2r1, x2, r2) - r2^2
eq3 = dist(a, 0, b, 2r1, -x3, 2r1 - r3) - r3^2
eq4 = dist(-a, 0, b, 2r1, x2, r2) - r2^2
eq5 = dist(-a, 0, b, 2r1, x3, 2r1 - r3) - r3^2;

function driver(r2, r3)
    function H(u)
        (a, b, r1, x2, x3) = u
        return [
            dist(a, 0, b, 2r1, 0, r1) - r1^2,
            dist(a, 0, b, 2r1, x2, r2) - r2^2,
            dist(a, 0, b, 2r1, -x3, 2r1 - r3) - r3^2,
            dist(-a, 0, b, 2r1, x2, r2) - r2^2,
            dist(-a, 0, b, 2r1, x3, 2r1 - r3) - r3^2
        ]
    end;

    iniv = BigFloat[1.52612, 0.65526, 1, 0.38904, -0.38904]
    nls(H, ini=iniv)[1]
end;

たとえば，甲円の直径が 2, 乙円の直径が 1.4 のとき，大円の直径は 2.92066 である。

function draw(r2, r3, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (a, b, r1, x2, x3) =  driver(r2, r3)
    @printf("甲円の直径が %g, 乙円の直径が %g のとき，大円の直径は %g である。\n", 2r2, 2r3, 2r1)
    @printf("r2 = %g;  r3 = %g;  a = %g;  b = %g;  r1 = %g;  x2 = %g;  x3 = %g\n", r2, r3, a, b, r1, x2, x3)
    plot([a, b, -b, -a, a], [0, 2r1, 2r1, 0, 0], color=:green, lw=0.5)
    circle(0, r1, r1)
    circle(x2, r2, r2, :blue)
    circle(x3, 2r1 - r3, r3, :magenta)
    segment(b, 2r1, -a, 0, :orange)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, r1, "大円:r1,(0,r1)", :red, :center, delta=-delta/2)
        point(x2, r2, "甲円:r2,(x2,r2)", :blue, :center, delta=-delta/2)
        point(x3, 2r1-r3, "乙円:r3,(x3,2r1-r2)", :magenta, :center, delta=-delta/2)
        point(0, 2r1, "2r1", :green, :center, :bottom, delta=delta/2)
        point(b, 2r1, "(b,2r1)", :green, :center, :bottom, delta=delta/2)
        point(a, 0, " a", :green, :center, :bottom, delta=delta/2)
    end  
end;

draw(1, 0.7, true)

算額（その1557）

算額（その1557）

四十九 岩手県一関市弥栄 弥栄長安寺 明治20年(1887)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，外円
#Julia, #SymPy, #算額, #和算, #数学

大円の中に弦を隔てて中円，小円を容れる。「弦の半分の二乗」と「(中円の直径)と(小円の直径の2倍)の和（注）」が等しく，大円，中円，小円の直径が無奇零数（整数）になる解を求めよ。

注：算額には，「外円径与中円二段相併」とあるが，そもそも外円は図にないし，ほかのところでは大円，中円，小円と呼んでいる。山村も「外円は大円の誤記」と指摘しているが，根本的におかしい。「大円径与中円二段相併」が条件のとき，無奇零数の解はない。山村はこれらの条件を無視して,「(4/2)^2=8」などとむちゃくちゃに数字をいじり，「大円径与中円二段相併」の条件を無視して，怪我の功名で「大円径=6，中円径=4，小円径=2」を出している。困ったものだ。

「(中円の直径)と(小円の直径の2倍)の和」の誤記だとすれば，唯一の無奇零数の解が得られる。

大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, r1 - R)
小円の半径と中心座標を r2, (0, R - r1)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r1::positive, r2::positive;
# eq1 = (R^2 - (R - 2r2)^2) - (2R + 4r1)  # 算額通り
eq1 = (R^2 - (R - 2r2)^2) - (2r1 + 4r2)   # 算額は誤記であると解釈
eq2 = (r1 + r2) - R
res = solve([eq1, eq2], (r1, r2))[2]  # 2 of 2

    (R/2 + sqrt(4*R^2 - 12*R + 1)/4 + 1/4, R/2 - sqrt(4*R^2 - 12*R + 1)/4 - 1/4)

# r1: 中円の半径
res[1](R => 6//2) |> println

    2

# r2: 小円の半径
res[2](R => 6//2) |> println

    1

検算：　(弦/2)^2 = 8;  中円の直径 + 2*小円の直径 = 8

大円，中円，小円の直径はそれぞれ，6，4，2 である。

function draw(R, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (r1, r2) = (R/2 + sqrt(4*R^2 - 12*R + 1)/4 + 1/4, R/2 - sqrt(4*R^2 - 12*R + 1)/4 - 1/4)
    @printf("(弦/2)^2 = %g;  中円の直径 + 2*小円の直径 = %g\n", R^2 - (R - 2r2)^2, 2r1 + 4r2)
    @printf("R = %g;  r1 = %g;  r2 = %g\n", R, r1, r2)

    plot()
    circle(0, 0, R)
    circle(0, R - r2, r2, :blue)
    circle(0, r1 - R, r1, :green)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, 0, "大円:R,(0,0)", :red, :center, delta=-delta/2)
        point(0, r1 - R, "中円:r1,(0,r1-R)", :green, :center, delta=-delta/2)
        point(0, R - r2, "小円:r2,(0,R-r2)", :blue, :center, delta=-delta/2)
    end  
end;

draw(6/2, true)

算額（その1556）

算額（その1556）

六十五 岩手県花泉町金沢 大門神社・大門観世音菩薩 明治33年(1900)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：球4個，3次元，盤上
#Julia, #SymPy, #算額, #和算, #数学

盤上に甲球が3個互いに接して載っており，その中央の隙間に乙球が入っている。乙球は盤に載っており，3 個の甲球に外接している。乙球の直径が 1 寸のとき，甲球の直径はいかほどか。

村山の図は，後ろの甲球が浮いているし，乙球が外に出てしまっている。

甲球の半径と中心座標を r1, (x11, 0, r1), (x12, r1, r1)
乙球の半径と中心座標を r2, (0, 0,0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1::positive, x11::positive,
      x12::negative, r2::positive;
eq1 = (x11 - x12)^2 + r1^2 - 4r1^2
eq2 = x12^2 + r1^2 + (r1 - r2)^2 - (r1 + r2)^2
eq3 = x11^2 + (r1 - r2)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (r1, x11, x12))[1]

    (3*r2, 2*sqrt(3)*r2, -sqrt(3)*r2)

甲球の半径は乙球の半径の 3 倍である。

function draw(r2, more)
    pyplot(size=(500, 250), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (r1, x11, x12) = (3*r2, 2*sqrt(3)*r2, -sqrt(3)*r2)
    p1 = plot()
    rotate(x11, 0, r1)
    circle(0, 0, r2, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0.8, 2.5, "上から見た図", mark=false)
    end  
    p2 = plot()
    circle(x12, r1, r1)
    circle(x11, r1, r1)
    circle(0, r2, r2, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(-2, 3.5, "y軸に平行な方向から見た図", mark=false)
    end  
    plot(p1, p2)
end;

draw(1/2, true)

 

 

算額（その1555）

算額（その1555）

六十三 岩手県花泉町 大門神社・大門観世音菩薩 明治13年(1880)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円7個，斜線2本
#Julia, #SymPy, #算額, #和算, #数学

大円と 2 本の斜線で区分される領域に 6 個の小円を描く。小円の直径が 1 寸のとき黄積はいかほどか。

大円の半径と中心座標を r1, (0, 0)
小円の半径と中心座標を r2, (r1 - r2, 0), (x2, y2), (x3, y3)
とおく。

「大円の直径はいかほどか」という場合は，算額（その1554）四十 岩手県一関市牧沢 牧沢八幡神社 明治5年(1872)の類題として解ける。この場合も，大円の直径は小円の直径の 4 倍である。

さて，山村は黄積を小円と大円の間にできる狭い領域（図のピンクと緑）も含めて色を塗っている。しかし，それでは答えが合わない。

正しくは，「日本の弦と小円の弧で囲まれる領域 ABCG の 2倍」である。OCE は ODG と相似なので，図に示した黄色の部分の面積は，「長方形 ABCD から，小円 1 個分の面積を差し引いた面積」である。

BC は小円の直径であるが，AB は何か?
三角形OCH において θ = ∠COH とすると，CH = sin(θ) = r2/3r2 = 1/3 なので θ = asin(1/3)， OC = 3r2*cos(θ) = 3r2*cos(asin(1/3)) = 2√2r2 である。BC は 4√2*r2 である。

長方形 ABCD の面積 = 2r2 * 2√2*2r2
小円 1 個分の面積 = πr2^2
黄積 = 「2*(長方形 ABCD の面積」 - 「小円 1 個分の面積」)
　　 = 2(2r2 * 2√2*2r2 - π*r2^2)
　　 = 2(8√2 - π)*r2^2
小円の半径が 1/2 のとき，黄積は 4.086057922697484 である。

r2 = 1/2
2(8√2 - π)*r2^2

    4.086057922697484

術は，「(√32 - 2*円積率)×小円径」で，円積率として π/4 を使い，小円の直径が 1 のとき，(√32 - 2*π/4)*1 = 4.086057922697484 で，答え 4.086余 となっている。

上述の結果と同じである。
山村は，オウム返しで術の解説をしているだけで，実際に解いていない。山村が理解した黄積で計算を進めたら，術と一致しないのだから。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::negative, r1::positive, r2::positive,
      x2::positive, y2::positive,
      x3::negative, y3::positive;
eq1 = -(r1 - 2r2)/a - r2/(r1 - r2)
eq2 = -r2/(r1 - r2 + a) - r2/(r1 - r2)
eq3 = x2^2 + y2^2 - (r1 - r2)^2
eq4 = (r1 - r2 - x2)^2 + y2^2 - 4r2^2
res = solve([eq1, eq2, eq3, eq4], (r1, a, x2, y2))[1]

    (4*r2, -6*r2, 7*r2/3, 4*sqrt(2)*r2/3)

大円の半径は，小円の半径の 4 倍である。

以下は，上下の円を描くために必要な円の中心を求めるための計算。

@syms θ
r1 = 4r2
a = -6*r2
θ = asin(r2/(r1 - r2 + a))
eq5 = x3^2 + y3^2 - (r1 - r2)^2
eq6 = dist2(a, 0, 0, a*tan(θ), x3, y3, r2)
res2 = solve([eq5, eq6], (x3, y3))[1]  # 1 of 3

    (-r2, 2*sqrt(2)*r2)

function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r1 = 4r2
    (r1, a, x2, y2) = (4*r2, -6*r2, 7*r2/3, 4*sqrt(2)*r2/3)
    (x3, y3) = (-r2, 2*sqrt(2)*r2)
    plot()
    circle(0, 0, r1, :magenta)
    circle2(r1 - r2, 0, r2)
    circle22(x2, y2, r2)
    circle22(x3, y3, r2)
    slope = tan(asin(r2/(r1 - r2 + a)))
    abline(a, 0, slope, 1.05a, r1 + 2r2, :green)
    abline(0, 0, -slope, 1.05a, r1 + 2r2, :blue)
    abline(2a, 0, -slope, 1.05a, r1 + 2r2, :blue)
    abline(a, 0, -slope, 1.05a, r1 + 2r2, :green)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(r1 - r2, 0, "r1-r2", :red, :center, delta=-delta/2)
        point(r1, 0, " r1", :red, :left, delta=-delta/2)
    end  
end;

draw(1/2, true)

算額（その1554）

算額（その1554）

四十 岩手県一関市牧沢 牧沢八幡神社 明治5年(1872)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図
https://w.atwiki.jp/sangaku/pages/308.html

山村の図は相変わらず不適切で，算額を解くための参考になりえない。

「今有如図」に基づいて算額を解く。

キーワード：円7個，斜線2本
#Julia, #SymPy, #算額, #和算

大円と 2 本の斜線で区分される領域に 6 個の小円を描く。小円の直径が 1 寸のとき大円の直径はいかほどか。

計算するまでもなく，適切な補助線を引くと答えがわかる。

図で，上側の緑の共通接線と平行な二本の青の線を引くと，大円の直径は小円の直径の 4 倍であることがわかる。

これを，SymPy で求めると以下のようになる。

大円の半径と中心座標を r1, (0, 0)
小円の半径と中心座標を r2, (r1 + r2, 0), (x2, y2), (x3, y3)
とおく。

include("julia-source.txt");

using SymPy
@syms a::negative, r1::positive, r2::positive,
      x2::positive, y2::positive,
      x3::negative, y3::positive;
eq1 = -(r1 - 2r2)/a - r2/(r1 + r2)
eq2 = -r2/(r1 + r2 + a) - r2/(r1 + r2)
eq3 = x2^2 + y2^2 - (r1 + r2)^2
eq4 = (r1 + r2 - x2)^2 + y2^2 - 4r2^2
res = solve([eq1, eq2, eq3, eq4], (r1, a, x2, y2))[1]

    (4*r2, -10*r2, 23*r2/5, 4*sqrt(6)*r2/5)

大円の半径は，小円の半径の 4 倍である。

以下は，上下の円を描くために必要な円の中心を求めるための計算。

@syms θ
r1 = 4r2
a = -10*r2
θ = asin(r2/(r1 + r2 + a))
eq5 = x3^2 + y3^2 - (r1 - r2)^2
eq6 = dist2(a, 0, 0, a*tan(θ), x3, y3, r2)
res = solve([eq5, eq6], (x3, y3))[1]  # 1 of 3

    (-3*r2/5, 6*sqrt(6)*r2/5)

function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r1 = 4r2
    (r1, a, x2, y2) = (4*r2, -10*r2, 23*r2/5, 4*sqrt(6)*r2/5)
    (x3, y3) = (-3*r2/5, 6*sqrt(6)*r2/5)
    θ = asin(r2/(r1 + r2 + a))
    println((sind(θ), cosd(θ)))
    plot()
    circle(0, 0, r1, :magenta)
    circle2(r1 + r2, 0, r2)
    circle22(x2, y2, r2)
    circle22(x3, y3, r2)
    slope = tan(asin(r2/(r1 + r2 + a)))
    abline(a, 0, slope, 1.05a, r1 + 2r2, :green)
    abline(0, 0, -slope, 1.05a, r1 + 2r2, :blue)
    abline(2a, 0, -slope, 1.05a, r1 + 2r2, :blue)
    abline(a, 0, -slope, 1.05a, r1 + 2r2, :green)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
    end  
end;

draw(1/2, true)

算額（その1553）

算額（その1553）

四 岩手県花巻市南笹間 東光寺慶応2年(1866)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円，多角形，矢
#Julia, #SymPy, #算額, #和算

正 n 角形に矢を n 本引き，内部に相似な正 n 角形を作る。外側の正 n 角形の一辺の長さと，内側の正 n 角形に内接する甲円の直径が与えられたとき，周辺の合同な三角形に内接する乙円の直径を求めよ。

外側の正 n 角形が内接する円の半径を R
外側の正 n 角形の一辺の長さを a, 矢の長さを b + c; BD = a, DA = BC = b, AC = c
甲円の半径を r
とおき，以下の連立方程式を解く。

n, a, r が既知である。

include("julia-source.txt");
# # julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

三角形 ABD において，∠DAB について第二余弦定理を適用して b を求める。

@syms n, a, b, c, R, r, r2
c = 2r*tand(Sym(180)/n)
R = a/2sind(Sym(180)/n)
eq1 = a^2 - (b^2 + (b + c)^2 - 2b*(b + c)*cosd(Sym(360)/n))
ans_b = solve(eq1, b)[2]
ans_b |> println
ans_b(n => 7, a => 5, r => 3).evalf() |> println

    -r*tan(pi/n) + sqrt((4*r^2*sin(pi/n)^4 + (a^2 - 4*r^2*tan(pi/n)^2)*cos(pi/n)^2)*tan(pi/n)^2)/(2*sin(pi/n)^2)
    3.47458828453188

丙円の半径を求める。
丙円が内接する三角形の面積を表す二通りの方程式が等しいとする。

s = (a + b + (b + c))/2
eq2 = (a + b + (b + c))*r2/2 - sqrt(s*(s- a)*(s - b)*(s - (b + c)));
eq2 = eq2(b => ans_b) |> simplify
ans_r2 = solve(eq2[1], r2)[1]
ans_r2 |> println
ans_r2(n => 7, a => 5, r => 3).evalf() |> println

    sqrt(2)*sqrt(-(-a^2*sin(pi/n)^2 + a^2 - 4*r^2*sin(pi/n)^2)^2/(cos(4*pi/n) - 1))*sin(pi/n)^2/(a*sin(pi/n)^2 + sqrt((a^2 - 4*r^2*sin(pi/n)^2)*sin(pi/n)^2))
    1.16507932205657

丙円の半径は，sin(pi/n)，cos(4*pi/n) の関数として表すことができる。

t = sin(π/n)^2
u = a^2 - 4t*r^2
r2 = √2t*sqrt((u - a^2*t)^2/(1 - cos(4π/n)))/(a*t + sqrt(t*u))

以下は，図を描くためだけに必要なもの。

@syms θb, a, b, c
eq3 = a^2 + (b + c)^2 -2a*(b + c)*cosd(θb) - b^2
ans_θb = solve(eq3, θb)[2]
ans_θb |> println

    180*acos((a^2 + 2*b*c + c^2)/(2*a*(b + c)))/pi

@syms x3, y3, x01, y01, x02, y02
eq4 = dist(x01, y01, x02, y02, x3, y3) - r2^2
eq5 = dist(x01, y01, 0, R, x3, y3) - r2^2
res_x3 = solve(eq4, x3)[2];
eq5 = eq5(x3 => res_x3) |> simplify |> numerator
res_y3 = solve(eq5, y3)[2]
res_y3 |> println
res_x3 |> println

    (-a*r2*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2) + a*x01*y01 - a*x02*y01 + 2*r2*y01*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2)*sin(pi/n) + r2*(y01 - y02)*sqrt(a^2 - 4*a*y01*sin(pi/n) + 4*x01^2*sin(pi/n)^2 + 4*y01^2*sin(pi/n)^2) - 2*x01*y01*y02*sin(pi/n) + 2*x02*y01^2*sin(pi/n))/(a*x01 - a*x02 - 2*x01*y02*sin(pi/n) + 2*x02*y01*sin(pi/n))
    (r2*sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2) - x01*y02 + x01*y3 + x02*y01 - x02*y3)/(y01 - y02)

function draw(n, a, r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    R = a/2sind(180/n)
    θ = 360/n
    θ2 = 90 .+ (0:θ:360)
    x = R.*cosd.(θ2)
    y = R.*sind.(θ2)
    b = -r*tan(pi/n) + sqrt((4*r^2*sin(pi/n)^4 + (a^2 - 4*r^2*tan(pi/n)^2)*cos(pi/n)^2)*tan(pi/n)^2)/(2*sin(pi/n)^2)
    c = 2r*tand(180/n)
    θb = 180*acos((a^2 + 2*b*c + c^2)/(2*a*(b + c)))/pi
    x01 = (b + c)*(cosd(θb + 180/n))
    y01 = R - (b + c)*sind(θb + 180/n)
    θ3 = atand(y01, x01)
    x2 = []
    y2 = []
    # r2 = sqrt(2)*sqrt(-(-a^2*sin(pi/n)^2 + a^2 - 4*r^2*sin(pi/n)^2)^2/(cos(4*pi/n) - 1))*sin(pi/n)^2/(a*sin(pi/n)^2 + sqrt((a^2 - 4*r^2*sin(pi/n)^2)*sin(pi/n)^2))
    t = sin(π/n)^2
    u = a^2 - 4t*r^2
    r2 = √2t*sqrt((u - a^2*t)^2/(1 - cos(4π/n)))/(a*t + sqrt(t*u))
    @printf("正%d角形の一辺の長さが %g，甲円の直径が %g のとき，乙円の直径は %g である。", n, a, 2r, 2r2)
    x02 = x[n]
    y02 = y[n]
    t = sqrt(x01^2 - 2*x01*x02 + x02^2 + y01^2 - 2*y01*y02 + y02^2)
    u = sin(pi/n)
    y3 = (-a*r2*t + a*x01*y01 - a*x02*y01 + 2*r2*y01*t*u + r2*(y01 - y02)*sqrt(a^2 - 4*a*y01*u + 4*x01^2*u^2 + 4*y01^2*u^2) - 2*x01*y01*y02*u + 2*x02*y01^2*u)/(a*x01 - a*x02 - 2*x01*y02*u + 2*x02*y01*u)
    x3 = (r2*t - x01*y02 + x01*y3 + x02*y01 - x02*y3)/(y01 - y02)
    l = c/2sind(180/n)
    for i = 1:n
        append!(x2, l*cosd(θ3))
        append!(y2, l*sind(θ3))
        θ3 += 360/n
    end
    plot()
    for i = 1:n
        segment(x[i], y[i], x[i + 1], y[i + 1], :green)
        segment(x[i], y[i], x2[i], y2[i], :green)      
    end
    circle(0, 0, R, :gray90)
    circle(0, 0, r, :blue)
    circle(0, 0, l, :gray90)
    rotate(x3, y3, r2, angle=360/n)
    if more        
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(x01, y01, " A", :green, :left, :vcenter)
        point(x2[2], y2[2], " C", :green, :left, :vcenter)
        point(0, R, "B", :green, :center, :bottom, delta=delta/2)
        point(x[n], y[n], " D", :green, :left, :vcenter)
    end
end;

draw(9, 5, 3.5, true)

和算の心（その010）

和算の心（その010）

等円術（II）：三斜等円術（一般公式）

米山忠興：等円術（II）：三斜等円術（一般公式），東洋大学紀要 自然科学編，第 50 号，P.107-121, 2006/03
https://toyo.repo.nii.ac.jp/record/2534/files/shizenkagakuhen50_107-121_OCR.pdf

等円が 2 個の場合

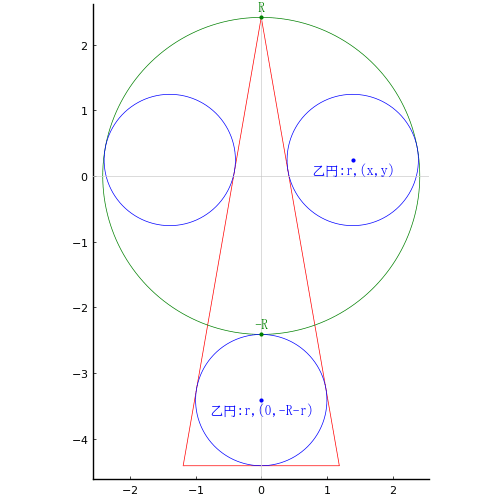
三角形内に界斜を引き，2 区分された領域に等円を入れる。大斜 = 9/2，中斜= 4，小斜 = 4 が与えられたとき，界斜はいかほどか。

結論

以下の公式を適宜使用する。

公式1: 界斜 = sqrt((中斜 + 小斜)^2 - 大斜^2)/2
公式2: 大斜 = sqrt((中斜 + 小斜)^2 - 4界斜^2)
公式3: 中斜 = sqrt(大斜^2 + 4界斜^2) - 小斜
公式4: 小斜 = sqrt(大斜^2 + 4界斜^2) - 中斜
公式5: 等円半径 = sqrt((大斜 + 中斜 + 小斜)(大斜 - 中斜 + 小斜)(中斜 - 大斜 + 小斜)(大斜 + 中斜 - 小斜))/(2(中斜 + 大斜 + 小斜 + 2*界斜))
公式6-1: x = (中斜^2 + 大斜^2 - 小斜^2)/(2大斜)
公式6-2: y = sqrt((中斜 + 大斜 + 小斜)(大斜 - 中斜 + 小斜)(中斜 - 大斜 + 小斜)(大斜 + 中斜 - 小斜))/(2大斜)
公式7-1: 大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
公式7-2: 大斜*(中斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
公式8-1: r*(x + sqrt(x^2 + y^2))/y
公式8-2: (-a*r + a*y + r*x + r*sqrt(a^2 - 2*a*x + x^2 + y^2))/y

公式を導く手順

大斜，中斜，小斜，界斜を変数名として，
等円の半径と中心座標を r, (x1, r), (x2, r)
三角形の頂点座標を (x, y)
界斜と大斜の交点座標を (a, 0) として，以下の手順により界斜のほか，等円の直径，等円の中心座標などを求める。

まず，大斜，中斜，小斜，界斜の相互関係を表す恒等式を導く。

求めるパラメータ以外の未知パラメータ a, r を消去する。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r::positive, a::positive, x::positive, y::positive, x1::positive,
      x2::positive, 大斜::positive, 中斜::positive, 小斜::positive, 界斜::positive;

eq1 = r*(小斜 + a + 界斜) - a*y
eq2 = r*(界斜 + (大斜 - a) + 中斜)- (大斜 - a)*y;

eq1, eq2 を辺々割って eq3 とする。

# eq3 = eq1.lhs/eq2.lhs - eq1.rhs/eq2.rhs  # こうしてもよいが
eq3 = (a + 小斜 + 界斜)/(中斜 + 大斜 + 界斜 - a) - a/(大斜 - a);
ans_a = solve(eq3, a)[1];

ans_a |> println
ans_a(大斜 => 4.5, 中斜 => 4, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
    2.06798918304242

注：ここで計算される a は大斜の左端点からの距離（左端点を原点とした）距離なので，中斜が左側にあるときには図を描くときに注意すること。

eq8 = y^2 + x^2 - 小斜^2
eq9 = y^2 + (a - x)^2 - 界斜^2
eq10 = y^2 + (大斜 - x)^2 - 中斜^2
eq10 |> println

    y^2 - 中斜^2 + (-x + 大斜)^2

eq11 = eq9 - eq8 |> expand
eq11 |> println

    a^2 - 2*a*x + 小斜^2 - 界斜^2

eq12 = eq10 - eq8 |> expand
eq12 |> println

    -2*x*大斜 - 中斜^2 + 大斜^2 + 小斜^2

eq1112 = 2a*x/(2大斜*x) - (小斜^2 + a^2 - 界斜^2)/(大斜^2 - 中斜^2 + 小斜^2)
eq1112 = eq1112(a => ans_a) |> simplify
eq1112 |> println

    (-大斜^2*(小斜 + 界斜)^2 + (小斜 + 界斜)*(中斜 + 小斜 + 2*界斜)*(-中斜^2 + 大斜^2 + 小斜^2) + (-小斜^2 + 界斜^2)*(中斜 + 小斜 + 2*界斜)^2)/((中斜 + 小斜 + 2*界斜)^2*(-中斜^2 + 大斜^2 + 小斜^2))

大斜，中斜，小斜，界斜の 4 変数を含む式は
(-大斜^2*(小斜 + 界斜)^2 + (小斜 + 界斜)*(中斜 + 小斜 + 2*界斜)*(-中斜^2 + 大斜^2 + 小斜^2) + (-小斜^2 + 界斜^2)*(中斜 + 小斜 + 2*界斜)^2)/((中斜 + 小斜 + 2*界斜)^2*(-中斜^2 + 大斜^2 + 小斜^2)) = 0
となる。

この式のうち，3 個に実際の値を与えて 4 番目の変数が取るべき値（解）を求めることができる。

1.　大斜，中斜，小斜をあたえて，界斜を求める

ans_界斜 = solve(eq1112, 界斜)[1]
ans_界斜 |> println
ans_界斜(大斜 => 4.5, 中斜 => 4, 小斜 => 3).evalf() |> println

    sqrt(中斜^2 + 2*中斜*小斜 - 大斜^2 + 小斜^2)/2
    2.68095132369090

公式1: 界斜 = sqrt((中斜 + 小斜)^2 - 大斜^2)/2

2.　中斜，小斜，界斜を与えて，大斜を求める

ans_大斜 = solve(eq1112, 大斜)[1]
ans_大斜 |> println
ans_大斜(中斜 => 4, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    sqrt(中斜^2 + 2*中斜*小斜 + 小斜^2 - 4*界斜^2)
    4.50000000000000

公式2: 大斜 = sqrt((中斜 + 小斜)^2 - 4界斜^2)

3.　大斜，小斜，界斜を与えて，中斜を求める

ans_中斜 = solve(eq1112, 中斜)[1]
ans_中斜 |> println
ans_中斜(大斜 => 4.5, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    -小斜 + sqrt(大斜^2 + 4*界斜^2)
    4.00000000000000

公式3: 中斜 = sqrt(大斜^2 + 4界斜^2) - 小斜

4.　大斜，中斜，界斜を与えて，小斜を求める

ans_小斜 = solve(eq1112, 小斜)[1]
ans_小斜 |> println
ans_小斜(大斜 => 4.5, 中斜 => 4, 界斜 => 2.68095132369090) |> println

    -中斜 + sqrt(大斜^2 + 4*界斜^2)
    3.00000000000000

公式4: 小斜 = sqrt(大斜^2 + 4界斜^2) - 中斜

5.　等円の半径を求める

eq1, eq2 による三角形の面積とヘロンの公式による面積が等しいとする連立方程式から，等円の半径 r を求めることができる。

@syms r
s = (大斜 + 中斜 + 小斜)/2
eq21 = (r*(小斜 + a + 界斜) + r*(界斜 + (大斜 - a) + 中斜)) - (大斜 - a)*y
eq22 = sqrt(s*(s - 大斜)*(s - 中斜)*(s - 小斜)) - (大斜 - a)*y/2;
res = solve([eq21, eq22], (r, y));
res[r] |> println
res[r](大斜 => 4.5, 中斜 => 4, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    sqrt(中斜 + 大斜 + 小斜)*sqrt(-中斜^3 + 中斜^2*大斜 + 中斜^2*小斜 + 中斜*大斜^2 - 2*中斜*大斜*小斜 + 中斜*小斜^2 - 大斜^3 + 大斜^2*小斜 + 大斜*小斜^2 - 小斜^3)/(2*中斜 + 2*大斜 + 2*小斜 + 4*界斜)
    0.697585939193294

公式5: 等円半径 = sqrt((大斜 + 中斜 + 小斜)*(大斜 - 中斜 + 小斜)*(中斜 - 大斜 + 小斜)*(大斜 + 中斜 - 小斜))/(2*(中斜 + 大斜 + 小斜 + 2*界斜))

6.　三角形の頂点座標 (x, y) を求める

x, y は，以下の連立方程式で求めることができる。

eq21 = x^2 + y^2 - 中斜^2
eq22 = (大斜 - x)^2 + y^2 - 小斜^2
res2 = solve([eq21, eq22], (x, y))[1];

# x
res2[1] |> println
res2[1](大斜 => 4.5, 中斜 => 4, 小斜 => 3) |> println

    (中斜^2 + 大斜^2 - 小斜^2)/(2*大斜)
    3.02777777777778

公式6-1: x = (中斜^2 + 大斜^2 - 小斜^2)/(2大斜)

# y
res2[2] |> println
res2[2](大斜 => 4.5, 中斜 => 4, 小斜 => 3) |> println

    sqrt(-(中斜 - 大斜 - 小斜)*(中斜 - 大斜 + 小斜)*(中斜 + 大斜 - 小斜))*sqrt(中斜 + 大斜 + 小斜)/(2*大斜)
    2.61391693219105

公式6-2: y = sqrt((中斜 + 大斜 + 小斜)(大斜 - 中斜 + 小斜)*(中斜 - 大斜 + 小斜)*(大斜 + 中斜 - 小斜))/(2大斜)

7.　a を求める    界斜と大斜の交点座標(a, 0)

小斜が左側にある場合

ans_a |> println
ans_a(大斜 => 4.5, 中斜 => 4, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
    2.06798918304242

公式7-1: 大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜)

中斜が左側にある場合には ans_a = 大斜 - 大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜) = 大斜*(中斜 + 界斜)/(中斜 + 小斜 + 2*界斜)

ans_a = 大斜 - 大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜) |> simplify
ans_a |> println
ans_a(大斜 => 4.5, 中斜 => 4, 小斜 => 3, 界斜 => 2.68095132369090) |> println

    大斜*(中斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
    2.43201081695758

公式7-2: 大斜*(中斜 + 界斜)/(中斜 + 小斜 + 2*界斜)

8.　等円の中心座標 (x1, r), (x2, r)

eq41 = dist2(0, 0, x, y, x1, r, r)
eq42 = dist2(a, 0, x, y, x2, r, r)
res3 = solve([eq41, eq42], (x1, x2))[4]  # 4 of 4

    (r*(x/y + sqrt(x^2 + y^2)/y), r*sqrt(a^2 - 2*a*x + x^2 + y^2)/y + (-a*r + a*y + r*x)/y)

公式8-1: r*(x + sqrt(x^2 + y^2))/y
公式8-2: (-a*r + a*y + r*x + r*sqrt(a^2 - 2*a*x + x^2 + y^2))/y

res3[1](a => 2.43201081695758, x => 3.0277777777777777, y => 2.613916932191048, r => 0.6975859391932936) |> println
res3[2](a => 2.43201081695758, x => 3.0277777777777777, y => 2.613916932191048, r => 0.6975859391932936) |> println

    1.87552974663334
    3.30648107032424

界斜f(大斜, 中斜, 小斜) = sqrt((中斜 + 小斜)^2 - 大斜^2)/2
大斜f(中斜, 小斜, 界斜) = sqrt((中斜 + 小斜)^2 - 4界斜^2)
中斜f(大斜, 小斜, 界斜) = sqrt(大斜^2 + 4界斜^2) - 小斜
小斜f(大斜, 中斜, 界斜) = sqrt(大斜^2 + 4界斜^2) - 中斜
等円半径f(大斜, 中斜, 小斜, 界斜) = sqrt((大斜 + 中斜 + 小斜)*(大斜 - 中斜 + 小斜)*(中斜 - 大斜 + 小斜)*(大斜 + 中斜 - 小斜))/(2*(中斜 + 大斜 + 小斜 + 2*界斜))
xf(大斜, 中斜, 小斜) = (中斜^2 + 大斜^2 - 小斜^2)/(2大斜)
yf(大斜, 中斜, 小斜) = sqrt((中斜 + 大斜 + 小斜)*(大斜 - 中斜 + 小斜)*(中斜 - 大斜 + 小斜)*(大斜 + 中斜 - 小斜))/(2大斜)
af1(大斜, 中斜, 小斜, 界斜) = 大斜*(小斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
af2(大斜, 中斜, 小斜, 界斜) = 大斜*(中斜 + 界斜)/(中斜 + 小斜 + 2*界斜)
x1f(a, x, y, r) = r*(x/y + sqrt(x^2 + y^2)/y)
x2f(a, x, y, r) = r*sqrt(a^2 - 2*a*x + x^2 + y^2)/y + (-a*r + a*y + r*x)/y;

界斜f(4.5, 4, 3) |> println
大斜f(4, 3, 2.68095132369090) |> println
中斜f(4.5, 3, 2.68095132369090) |> println
小斜f(4.5, 4, 2.68095132369090) |> println
等円半径f(4.5, 4, 3, 2.68095132369090) |> println
xf(4.5, 4, 3) |> println
yf(4.5, 4, 3) |> println
af1(4.5, 4, 3, 2.68095132369090) |> println
af2(4.5, 4, 3, 2.68095132369090) |> println
x1f(2.43201081695758, 3.0277777777777777, 2.613916932191048, 0.6975859391932936) |> println
x2f(2.43201081695758, 3.0277777777777777, 2.613916932191048, 0.6975859391932936) |> println

    2.680951323690902
    4.500000000000004
    3.9999999999999973
    2.9999999999999973
    0.6975859391932936
    3.0277777777777777
    2.613916932191048
    2.0679891830424224
    2.432010816957577
    1.875529746633338
    3.3064810703242418

大斜, 中斜, 小斜 がそれぞれ 4.5, 4, 3 のとき，
界斜 = 2.68095;  r = 0.697586;  a = 2.43201;  x = 3.02778;  y = 2.61392;  x1 = 1.87553;  x2 = 3.30648
である。

算額の術では 界斜 = sqrt((中斜 + 小斜)^2 - 大斜^2)/2 となっており，正しい答えが求まっていることがわかる。

function draw(more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    (大斜, 中斜, 小斜) = (9//2, 4, 3)
    界斜 = 界斜f(4.5, 4, 3)
    r = 等円半径f(4.5, 4, 3, 界斜)
    x = xf(大斜, 中斜, 小斜)
    y = yf(大斜, 中斜, 小斜)
    a = af2(大斜, 中斜, 小斜, 界斜)
    x1 = x1f(a, x, y, r)
    x2 = x2f(a, x, y, r)
    @printf("界斜 = %g;  r = %g;  a = %g;  x = %g;  y = %g;  x1 = %g;  x2 = %g\n", 界斜, r, a, x, y, x1, x2)
    plot([0, 大斜, x, 0], [0, 0, y, 0], color=:black, lw=0.5)
    circle(x1, r, r)
    circle(x2, r, r)
    segment(a, 0, x, y, :blue)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /  3  # size[2] * fontsize * 2
        point(大斜, 0, " 大斜", :black, :left, :bottom, delta=delta)
        point(x, y, " (x,y)", :black, :left, :vcenter, delta=-delta)
        point(x1, r, "(x1,r)", :red, :center, delta=-delta)
        point(x2, r, "(x2,r)", :red, :center, delta=-delta)
        point(a, 0, " a", :black, :left, :bottom, delta=delta)
        point(x/2, 2y/3, "中斜", :black, :left, mark=false)
        point((大斜 + x)/2, 2y/3, "小斜", :black, :left, mark=false)
        point((a + x)/2, 2y/3, "  界斜", :blue, :left, mark=false)
        vline!([0], color=:black, lw=0.5)
        hline!([0], color=:black, lw=0.5)
        plot!(xlims=(0, 5))
    else
        plot!(showaxis=false)
    end
end;

draw(true)

算額（その1552）

算額（その1552）

八十 群馬県群馬郡榛名町榛名山 榛名神社 安政3年(1856)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：扇型の面積の和，等円，白積，黒積
#Julia, #SymPy, #算額, #和算，#数学

面積が同じの等円を互い外接するように並べ，接点を境に黒白で塗り分ける。黒く塗られた部分の面積の和が与えられたとき，白く塗られた部分の面積はいかほどか。

円の中心を結ぶ n 多角形の内角の和は (n - 2)π = (n - 2)*360° である。
等円の半径を r とおくと，n に関係なく，常に以下が成り立つ。

using SymPy
@syms n, r;

等円積 = PI*r^2
等円積 |> println

    pi*r^2

黒積 = (n - 2)//2*PI*r^2 |> simplify
黒積 |> println

    pi*r^2*(n - 2)/2

白積 = n*等円積 - 黒積 |> simplify
白積 |> println

    pi*r^2*(n + 2)/2

白積は，「等円積の n 倍から黒積を差し引いたもの」であるが，

白積 - 黒積 |> simplify |> println

    2*pi*r^2

白積は黒積より（円の個数にかかわらず，常に）等円 2 個分の面積だけ大きい。

0.1.　左側の場合

n = 4
等円積 = PI*r^2
黒積 = 等円積*(103 + 77 + 104 + 76)/360;
黒積 |> println

    pi*r^2

白積 = 等円積*((360 - 103) + (360 - 77) + (360 - 104) + (360 - 76))/360
白積 |> println

    3*pi*r^2

白積 - 黒積 |> println

    2*pi*r^2

0.2.　右側の場合

n = 7
等円積 = PI*r^2
黒積 = 等円積*(100 + 220 + 78 + 124 + 128 + 153 + 97)/360
黒積 |> println

    5*pi*r^2/2

白積 = 等円積*((360 - 100) + (360 - 220) + (360 - 78) + (360 - 124) + (360 - 128) + (360 - 153) + (360 - 97)) ./360
白積 |> println

    9*pi*r^2/2

白積 - 黒積 |> println

    2*pi*r^2

 

亡き妻へ求めし庭の福寿草今一輪になりにけるかな

算額（その1551）

算額（その1551）

百四十六 群馬県新田郡新田町下田中 田中神社 大正6年(1917)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：連立方程式
#Julia, #SymPy, #算額, #和算，#数学

合計 244 坪の土地を，甲乙 2 つに分筆する。（面積を正方形に換算すると，）乙の正方形の一辺は甲のそれよりも 2 間短い。甲乙それぞれの一辺の長さはいかほどか。

using SymPy
@syms 甲::positive, 乙::positive
eq1 = 甲^2 + 乙^2 - 244
eq2 = (甲 - 2) - 乙
solve([eq1, eq2], (甲, 乙))[1]

    (12, 10)

 

算額（その1550）

算額（その1550）

百二十四 群馬県桐生市天神町 天満宮 明治11年(1878)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：連立方程式，整数方程式
#Julia, #SymPy, #算額, #和算，#数学

桃と梨を買った。桃と梨の両方合わせた個数と代金（の数値）が同じになった。ただし，桃は 9 個で代金は 5 文，梨は 3 個で 25 文である。個数と代金を求めよ。

using SymPy
@syms 桃, 梨
eq = (5(桃/9) + 25(梨/3)) - (桃 + 梨)

数学の試験ならいざ知らず，ブルートフォースで一発即答。

for 桃 = 9:9:1000, 梨 = 3:3:1000
    (5(桃/9) + 25(梨/3)) == (桃 + 梨) && (println("桃 = $桃 個，代金 = $(5(桃/9))\n梨 = $梨 個，代金 = $(25(梨/3))"); break)
end

    桃 = 99 個，代金 = 55.0
    梨 = 6 個，代金 = 50.0