かなり久しぶりの現実逃避シリーズですが、
当初の予定を変更し、判断推理に限定しないことにしました。
もうすぐ年も明け、受験生の皆様は戦争も佳境に入っている事と思う。
入試は時間との戦いでもある。
特に数学なんかは、教科書通りの解法で本当に良いのか。
教科書の解法よりも早く解く方法があるのではないか。
それが正に「濃度」の問題である。
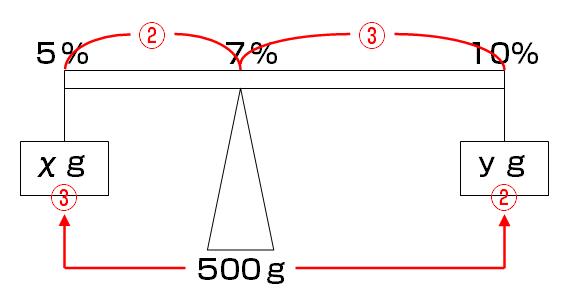
濃度の問題といえば、例えばこんな感じだと思う。
【例題】
5%の食塩水Aと10%の食塩水Bがある。
この食塩水A、Bすべて混ぜたら、7%の食塩水が500gできた。
A、Bそれぞれ何gずつ混ぜたのかを求めよ。
これを教科書通りに解くには「連立方程式」を立てなければならない。
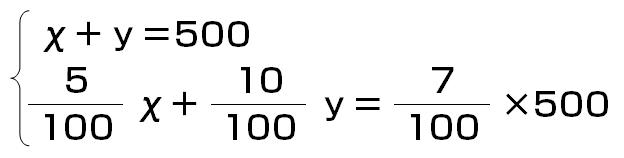
これでは急いで解いても1分はかかるだろう。
だが、「食塩水天秤」を使えばこんな感じ。30秒足らずで解けてしまうのだ。

もう上の図を見ただけで大体お分かりかと思うが、
食塩水天秤のポイントは、
(1)支点に混ぜた後の食塩水の濃度を書く
(2)両サイドに混ぜる食塩水の濃度を書く
(3)支点からの距離の比率を書く(2:3)
(4)混ぜた後の食塩水の重さを支点からの距離の逆比で配分する(3:2)
つまり500gを3:2に配分して300gと200g。ハイ終了。
正解:A300g、B200g
早い、早すぎる……
連立方程式とは何だったのか。
なぜこんな方法で解けるのかと言うと、
天秤は【荷重×支点からの距離】が左右で等しければ釣り合うのは学校で学んだと思う。
実は、食塩水の重さを荷重に、濃度を距離に置き換えただけで理屈は一緒なのだ。
荷重(g)×支点からの距離(cm)=回転する力(g)
食塩水(g)×濃度(%)=食塩(g)
ほら、何となく一緒でしょ?(雑になってきた)
ではいよいよ実践問題。もう寝たいから1問だけやって終わりにします。
【問題1】
次の□にあてはまる数を求めなさい。
10%の食塩水□gに200gの水を加えると6%の食塩水になる。
天秤はこう描きます。
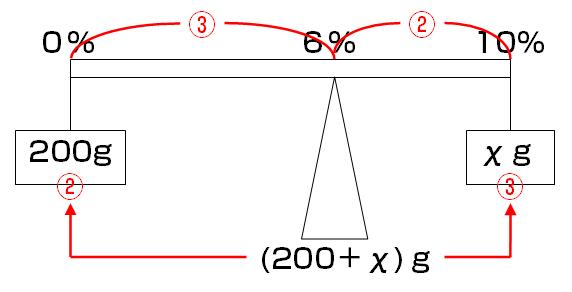
つまりこうなる。
(200+χ)×(2/5)=200
χ=300
終了。
正解:300
当初の予定を変更し、判断推理に限定しないことにしました。
もうすぐ年も明け、受験生の皆様は戦争も佳境に入っている事と思う。
入試は時間との戦いでもある。
特に数学なんかは、教科書通りの解法で本当に良いのか。
教科書の解法よりも早く解く方法があるのではないか。
それが正に「濃度」の問題である。
濃度の問題といえば、例えばこんな感じだと思う。
【例題】
5%の食塩水Aと10%の食塩水Bがある。
この食塩水A、Bすべて混ぜたら、7%の食塩水が500gできた。
A、Bそれぞれ何gずつ混ぜたのかを求めよ。
これを教科書通りに解くには「連立方程式」を立てなければならない。
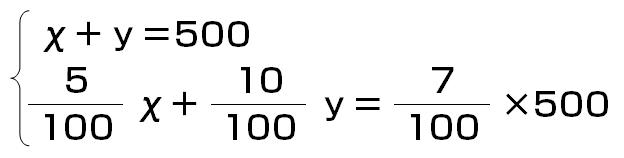
これでは急いで解いても1分はかかるだろう。
だが、「食塩水天秤」を使えばこんな感じ。30秒足らずで解けてしまうのだ。

もう上の図を見ただけで大体お分かりかと思うが、
食塩水天秤のポイントは、
(1)支点に混ぜた後の食塩水の濃度を書く
(2)両サイドに混ぜる食塩水の濃度を書く
(3)支点からの距離の比率を書く(2:3)
(4)混ぜた後の食塩水の重さを支点からの距離の逆比で配分する(3:2)
つまり500gを3:2に配分して300gと200g。ハイ終了。
正解:A300g、B200g
早い、早すぎる……
連立方程式とは何だったのか。
なぜこんな方法で解けるのかと言うと、
天秤は【荷重×支点からの距離】が左右で等しければ釣り合うのは学校で学んだと思う。
実は、食塩水の重さを荷重に、濃度を距離に置き換えただけで理屈は一緒なのだ。
荷重(g)×支点からの距離(cm)=回転する力(g)
食塩水(g)×濃度(%)=食塩(g)
ほら、何となく一緒でしょ?(雑になってきた)
ではいよいよ実践問題。もう寝たいから1問だけやって終わりにします。
【問題1】
次の□にあてはまる数を求めなさい。
10%の食塩水□gに200gの水を加えると6%の食塩水になる。
天秤はこう描きます。

つまりこうなる。
(200+χ)×(2/5)=200
χ=300
終了。
正解:300




















※コメント投稿者のブログIDはブログ作成者のみに通知されます