算額（その225）

算額（その225）

バージョンアップ https://blog.goo.ne.jp/r-de-r/e/b049f677e607ba6a92b04bb805ae3b0f

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（205）
長野県千曲市八幡 八幡八幡神社 文久2年(1862)

基本的に，算額（その22）と同じである。

岩手県遠野市附馬牛町 早池峰神社
http://www.wasan.jp/iwate/hayatine.html

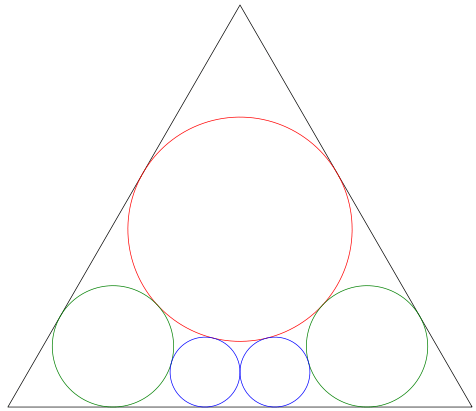
三角形の中に天円，地円，無名円 5 個が入っている。天円の径が 1 寸のとき，地円の径はいかほどか。

図のように記号を定める。
天円の半径，中心座標を r1, (0, y1)
地円の半径，中心座標を r2, (x2, y2)
無名円の半径，中心座標を r3, (r3, r3)
とする。

以下の連立方程式を立て，nlsolve() で数値解を求める。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms r1::positive, y1::positive, r2::positive, x2::positive, r3::positive, x0::positive, y0::positive;

r1 = 1
y0 = sqrt(Sym(3)) * x0
eq1 = r3^2 + (y1 - r3)^2 - (r1 + r3)^2
eq2 = (x2 - r3)^2 + (r2 - r3)^2 - (r2 + r3)^2
eq3 = x2^2 + (y1 - r2)^2 - (r1 + r2)^2
eq4 = distance(x0, 0, 0, y0, 0, y1) - r1^2
eq4 = (y0 - y1)/2 - r1  # 角度がわかっているので簡単になる
eq4 = 3x0^2 - (y1 + 2)^2  # 更に平方根をなくす
eq5 = distance(x0, 0, 0, y0, x2, r2) - r2^2
eq5 = (x0 - x2)/sqrt(Sym(3)) - r2
eq5 = (x0 -x2)^2 - 3r2^2;  # 平方根をなくす

円の中心から三角形の斜辺までの距離が円の半径に等しいとする eq4, eq5 は，この三角形が正三角形であることから，簡約化できる。また，solve() でどの変数について解くかというリストを付けなければ，
res = solve([eq1, eq2, eq3, eq4, eq5])
で数式解を求めることはできる。

res = solve([eq1, eq2, eq3, eq4, eq5])

   1-element Vector{Dict{Any, Any}}:
    Dict(x0 => (-7259*sqrt(12519 + 7228*sqrt(3)) - 4187*sqrt(37557 + 21684*sqrt(3)) + 662827*sqrt(3) + 1148053)/(-47*sqrt(39)*sqrt(963 + 556*sqrt(3)) - 74*sqrt(13)*sqrt(963 + 556*sqrt(3)) + 12279 + 7092*sqrt(3)), r3 => -5*sqrt(37557 + 21684*sqrt(3))/26 - 3*sqrt(12519 + 7228*sqrt(3))/13 + 89/2 + 26*sqrt(3), r2 => (-18582228589*sqrt(37557 + 21684*sqrt(3))/13 - 32185364034*sqrt(12519 + 7228*sqrt(3))/13 + 391757368513 + 226181222168*sqrt(3))/(-20717394*sqrt(13)*sqrt(963 + 556*sqrt(3)) - 11961193*sqrt(39)*sqrt(963 + 556*sqrt(3)) + 1892677408*sqrt(3) + 3278213433), y1 => -sqrt(12519/4 + 1807*sqrt(3)) + 40 + 47*sqrt(3)/2, x2 => (-28787502 - 16620472*sqrt(3) + 2365076*sqrt(12519 + 7228*sqrt(3))/13 + 1365478*sqrt(37557 + 21684*sqrt(3))/13)/(-925*sqrt(39)*sqrt(963 + 556*sqrt(3)) - 1602*sqrt(13)*sqrt(963 + 556*sqrt(3)) + 146360*sqrt(3) + 253503))

例えば，r2 であれば，数式は
r2 => (-18582228589*sqrt(37557 + 21684*sqrt(3))/13 - 32185364034*sqrt(12519 + 7228*sqrt(3))/13 + 391757368513 + 226181222168*sqrt(3))/(-20717394*sqrt(13)*sqrt(963 + 556*sqrt(3)) - 11961193*sqrt(39)*sqrt(963 + 556*sqrt(3)) + 1892677408*sqrt(3) + 3278213433)
で，これはまさしく 0.541123647609847 を与える（以下の数値解とは若干異なる）。しかし，いずれにせよ r1 を未知としてそれぞれの解に r1 を含む形で解を得ようとすると，有限の時間内には解は求まらないようである。

そこで，いつもの対応で，nlsolve() で解を求めることにする。

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")

   r3^2 + (-r3 + y1)^2 - (r3 + 1)^2,
   (r2 - r3)^2 - (r2 + r3)^2 + (-r3 + x2)^2,
   x2^2 + (-r2 + y1)^2 - (r2 + 1)^2,
   3*x0^2 - (y1 + 2)^2,
   -3*r2^2 + (x0 - x2)^2,

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (y1, r2, x2, r3, x0) = u
   return [
       r3^2 + (-r3 + y1)^2 - (r3 + 1)^2,
       (r2 - r3)^2 - (r2 + r3)^2 + (-r3 + x2)^2,
       x2^2 + (-r2 + y1)^2 - (r2 + 1)^2,
       3*x0^2 - (y1 + 2)^2,
       -3*r2^2 + (x0 - x2)^2,
   ]
end;

iniv = [big"1.2", 0.5, 0.7, 0.2, 0.8]
res = nls(H, ini=iniv)
  (BigFloat[1.585776115068257755122089256490132844790684509754511012457580246715684326737859, 0.5411142703251270921419775369262249321419086495250945339808838737796209260247126, 1.133011396384708951545840117932571235121725730234141906521758307553018076355822, 0.3116714054876906382129734754350708014875244562726158413609579698585776388195518, 2.070248805288389105459538534628650709909693363683297092946397231160973369434497], true)

using Printf
(a1, a2, a3, a4, a5) = res[1]
@printf("y1 = %.7f,  r2 = %.7f;  x2 = %.7f; r3 = %.7f;  x0 = %.7f\n",
           a1, a2, a3, a4, a5)

   y1 = 1.5857761,  r2 = 0.5411143;  x2 = 1.1330114; r3 = 0.3116714;  x0 = 2.0702488

地円の径は 0.5411 寸，すなわち 5分4厘1毛1糸...である。

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function circle4(x, y, r, color=:red)
  circle(x, y, r, color)
  circle(x, -y, r, color)
  circle(-x, y, r, color)
  circle(-x, -y, r, color)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (y1, r2, x2, r3, x0) = res[1]
   r1 = 1
   y0 = sqrt(3) * x0
   @printf("y1 = %.7f;  r2 = %.7f;  x2 = %.7f;  r3 = %.7f;  x0 = %.7f;  y0 = %.7f\n", y1, r2, x2, r3, x0, y0)
   @printf("地円の径 = %.5f\n", r2)
   println("x0 = $x0")
   println(float(distance(x0, 0, 0, y0, 0, y1)))
   println("y0 = $y0\ny1 = $y1")
   println("y0 - y1 = $(y0 - y1)")
   plot([x0, 0, -x0, x0], [0, y0, 0, 0], color=:black, lw=0.5)
   circle(0, y1, r1)
   circle(x2, r2, r2, :green)
   circle(-x2, r2, r2, :green)
   circle(r3, r3, r3, :blue)
   circle(-r3, r3, r3, :blue)
   if more == true
       point(0, y1, " y1   天円", :red)
       point(x2, r2, "(x2,r2) 地円", :green, :center, :top)
       point(r3, r3, "(r3,r3)", :blue, :center, :top)
       point(x0, 0, " x0", :black ,:left, :bottom)
       point(0, y0, " y0", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その224）

算額（その224）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（201）
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

扇の面に大円，中円，小円が描かれている。扇の要から先端まで（扇骨の長さ）が 7寸9分6厘，大円の径が 5寸9分7厘であるとき，中円の径を求めよ。

図のように記号を定める。
扇面の外周円の半径（扇骨の長さ）を r0
要から扇の紙がはられていない部分の半径（図参照）を r4
大円の半径，中心座標を r1, (0, r0 - r1)
中円の半径，中心座標を r2, (x2, y2)
小円の半径，中心座標を r3, (x3, y3)
扇の右端の点（図参照）の座標を (x, y) とする。
ただし，r0 = 798, r1 = 597, r4 = r0 - 2r1 である。また，y = sqrt(r0^2 - x^2) である。 

以下の連立方程式を立て，nlsolve() で数値解を求める。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms r0::positive, r1::positive, r2::positive, r3::positive, r4::positive,
   x2::positive, y2::positive, x3::positive, y3::positive, x::positive, y::positive;

r0 = 796
r1 = 597 // 2
r4 = r0 - 2r1
y = sqrt(r0^2 - x^2)
eq1 = x3^2 + y3^2 - (r3 + r4)^2
eq2 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq3 = x3^2 + (r0 - r1 - y3)^2 - (r1 + r3)^2
eq4 = x2^2 + (r0 -r1 - y2)^2 - (r1 + r2)^2
eq5 = x2^2 + y2^2 - (r0 - r2)^2
eq6 = distance(0, 0, x, y, x2, y2) - r2^2
eq7 = distance(0, 0, x, y, x3, y3) - r3^2;

# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7])

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")

   x3^2 + y3^2 - (r3 + 199)^2,
   -(r2 + r3)^2 + (x2 - x3)^2 + (y2 - y3)^2,
   x3^2 + (995/2 - y3)^2 - (r3 + 597/2)^2,
   x2^2 + (995/2 - y2)^2 - (r2 + 597/2)^2,
   x2^2 + y2^2 - (796 - r2)^2,
   -r2^2 + x^2*(x*y2 - x2*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x2 + y2*sqrt(633616 - x^2))/633616 + x2)^2,
   -r3^2 + x^2*(x*y3 - x3*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x3 + y3*sqrt(633616 - x^2))/633616 + x3)^2,

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r2, x2, y2, r3, x3, y3, x) = u
   return [
       x3^2 + y3^2 - (r3 + 199)^2,
       -(r2 + r3)^2 + (x2 - x3)^2 + (y2 - y3)^2,
       x3^2 + (995/2 - y3)^2 - (r3 + 597/2)^2,
       x2^2 + (995/2 - y2)^2 - (r2 + 597/2)^2,
       x2^2 + y2^2 - (796 - r2)^2,
       -r2^2 + x^2*(x*y2 - x2*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x2 + y2*sqrt(633616 - x^2))/633616 + x2)^2,
       -r3^2 + x^2*(x*y3 - x3*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x3 + y3*sqrt(633616 - x^2))/633616 + x3)^2,
   ]
end;

iniv = [big"300.0", 400, 500, 150, 100, 100, 700]
res = nls(H, ini=iniv)

   (BigFloat[199.0000000000000000000000000000000000003059242582377957862817582029431903187704, 477.6000000000000000000000000000000000001229072112677520304477397424728031693592, 358.1999999999999999999999999999999999993269666318768492701801319535249814981402, 99.49999999999999999999999999999999999969321045225668210052457642746139024754251, 238.7999999999999999999999999999999999995707652750100779995615047089452401612384, 179.100000000000000000000000000000000000061357909548663579895084714507721987446, 759.5807976794579513846102530511571579906945490238112350429439611428561425365724], true)

using Printf
(a1, a2, a3, a4, a5, a6, a7) = res[1]
@printf("r2 = %.3f,  x2 = %.3f;  y2 = %.3f; r3 = %.3f;  x3 = %.3f;  y3 = %.3f; x = %.3f\n",
           a1, a2, a3, a4, a5, a6, a7)

   r2 = 199.000,  x2 = 477.600;  y2 = 358.200; r3 = 99.500;  x3 = 238.800;  y3 = 179.100; x = 759.581

r2 = 199.000;  x2 = 477.600;  y2 = 358.200
r3 =  99.500;  x3 = 238.800;  y3 = 179.100
r4 = 199.000;   x = 759.581;   y = 238.019
中円の径 = 2r2 = 398.000
小円の径 = 2r3 = 199.000

中円の直径は 398 寸である。

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function circle4(x, y, r, color=:red)
  circle(x, y, r, color)
  circle(x, -y, r, color)
  circle(-x, y, r, color)
  circle(-x, -y, r, color)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, x2, y2, r3, x3, y3, x) = res[1]
   r0 = 796
   r1 = 597//2
   r4 = r0 - 2r1
   y = sqrt(r0^2 - x^2)
   @printf("r2 = %.3f;  x2 = %.3f;  y2 = %.3f\nr3 =  %.3f;  x3 = %.3f;  y3 = %.3f\nr4 = %.3f;   x = %.3f;   y = %.3f\n",
           r2, x2, y2, r3, x3, y3, r4, x, y)
   @printf("中円の径 = 2r2 = %.3f\n小円の径 = 2r3 = %.3f\n", 2r2, 2r3)
   deg = atand(y/x)
   plot()
   circle(0, 0, r0, :black, beginangle=deg, endangle=180 - deg)
   circle(0, 0, r4, :black, beginangle=deg, endangle=180 - deg)
   circle(0, 0, r4/2, :black, beginangle=180 + deg, endangle=360 - deg)
   factor = r4/2 / r0
   segment(x, y, -x*factor, -y*factor)
   segment(-x, y, x*factor, -y*factor)
   circle(0, r0 - r1, r1)
   circle(x2, y2, r2, :green)
   circle(-x2, y2, r2, :green)
   circle(x3, y3, r3, :blue)
   circle(-x3, y3, r3, :blue)
   if more == true
       point(x, y, "(x,y)")
       point(0, r0 - r1, " 大円 r1", :red, :left, :bottom)
       point(0, r0 - r1, " r0-r1", :red)
       point(0, r0, " r0")
       point(0, r4, " r4")
       point(x2, y2, "(x2,y2)", :green, :center)
       point(x2, y2, "中円 r2", :green, :center, :bottom)
       point(x3, y3, "(x3,y3)", :blue, :center)
       point(x3, y3, "小円 r3", :blue, :center, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;