算額（その234）

算額（その234）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（223)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

算額（その4）を一段階複雑にしたものである。https://blog.goo.ne.jp/r-de-r/e/faa0efc125cc1b246538a9965949f782

正三角形と甲円，乙円，丙円，丁円がある。乙円，丁円の径がそれぞれ 16寸，9寸のとき，丙円の径を求めよ。

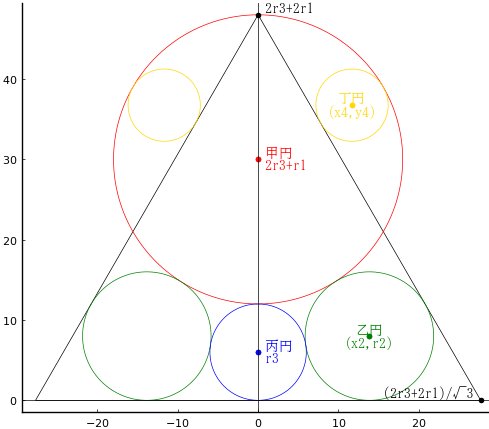
甲円の半径 r1, (0, 2r3 + r1),
乙円の半径 r2, (x2, r2),
丙円の半径 r3, (r3, r3),
丁円の半径 r4, (x4, y4), 
だたし，r2 = 16/2, r4 = 9/2
また，x4, y4 は r1, r3 から求めることができる

以下の方程式を解き，r1, r3, x2 を求める。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, r3::positive, r4::positive,
     x2::positive;

(r2, r4) = (16//2, 9//2)
eq1 = x2^2 + (r2 - r3)^2 - (r2 + r3)^2
eq2 = x2^2 + (2r3 + r1 - r2)^2 - (r1 + r2)^2
eq3 = r1 / 2 - 2r4;
solve([eq1, eq2, eq3], (r1, r3, x2))[1]

   (18, 6, 8*sqrt(3))

(r1, r3, x2) = (18, 6, 8*sqrt(3))

   (18, 6, 13.856406460551018)

ついで，x4, y4 を求める。

x4 = (r1*(3/4))*sqrt(3)/2
y4 = 2r3 + r1 + (r1*(3/4))/2
(x4, y4)

   (11.69134295108992, 36.75)

r1 = 18, r3 = 6, x2 = 13.8564065;  x4 = 11.6913430;  y4 = 36.75
丙円の半径 r3 = 6 なので，元の単位での直径は 12 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3, x2) = (18, 6, 8*sqrt(3))
   x4 = (r1*(3/4))*sqrt(3)/2
   y4 = 2r3 + r1 + (r1*(3/4))/2
   @printf("r1 = %.7f;  r3 = %.7f;  x2 = %.7f\n", r1, r3, x2)
   @printf("x4 = %.7f;  y4 = %.7f\n", x4, y4)
   y = 2r3 + 2r1
   x = y/sqrt(3)
   plot([x, 0, -x, x], [0, y, 0, 0], color=:black, lw=0.5)
   circle(0, 2r3 + r1, r1, :red)
   circle(x2, r2, r2, :green)
   circle(-x2, r2, r2, :green)
   circle(0, r3, r3, :blue)
   circle(x4, y4, r4, :gold)
   circle(-x4, y4, r4, :gold)
   if more == true
       point(0, 2r3 + r1, " 2r3+r1", :red)
       point(0, 2r3 + r1, " 甲円", :red, :left, :bottom)
       point(0, 2r3 + 2r1, " 2r3+2r1", :black, :left, :bottom)
       point((2r3 + 2r1)/√3, 0, "(2r3+2r1)/√3 ", :black, :right, :bottom)
       point(x4, y4, "(x4,y4)", :gold, :center)
       point(x4, y4, "丁円", :gold, :center, :bottom)
       point(0, r3, " r3", :blue)
       point(0, r3, " 丙円", :blue, :left, :bottom)
       point(x2, r2, "(x2,r2)", :green, :center)
       point(x2, r2, "乙円", :green, :center, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その233）

算額（その233）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（222)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

菱形の中に，大円，中円，小円が入っている。中円，小円の径がそれぞれ 8寸，4寸のとき，大円の径を求めよ。

大円の半径 r1, (r3 + r1, 0),
中円の半径 r2, (0, r3 + r2),
小円の半径 r3, (0, 0),
だたし，r2 = 8/2, r3 = 4/2。
以下の方程式を解く。

r2, r3 が与えられているとき，条件式は 1 つである。
r2, r3 が任意の値を取るとしてこの方程式を解くと r1 は r2, r3 を含む式になる。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, r3::positive;

(r2, r3) = (4, 2)
eq1 = (r3 + r1)^2 + (r3 + r2)^2 - (r1 + r2)^2
solve(eq1, r1)[1] |> println

   r3*(r2 + r3)/(r2 - r3)

すなわち，「中円と小円の半径の和を，中円と小円の半径の差で割り，小円の半径を掛ければ，大円の半径が得られる」
2 * (4 + 2) / (4 - 2) = 6 である。

大円の半径は6，すなわち元の単位での大円の直径は 12寸である。

外形の菱形を書くには，x軸上の頂点のx座標を x, y軸上の頂点のx座標を y として方程式を2本追加し，合わせて3本の連立方程式を解く。

ただし，r2, r3 が未知数のままだと solve() では解を求めることができないので，問にあるように r2 = 4, r3 = 2 の場合について解く。

using SymPy
@syms r1::positive, r2::positive, r3::positive, x::positive, y::positive;

(r2, r3) = (4, 2)
eq1 = (r3 + r1)^2 + (r3 + r2)^2 - (r1 + r2)^2
eq2 = distance(0, y, x, 0, r3 + r1, 0) - r1^2
eq3 = distance(0, y, x, 0, 0, r3 + r2) - r2^2;

res = solve([eq1, eq2, eq3], (r1, x, y))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (6, (13*sqrt(6) + 32)/(2*sqrt(7 - 2*sqrt(6))), 26/5 + 32*sqrt(6)/15)

x はもう少し簡単な式になる。

res[1][2] |> sympy.sqrtdenest |> simplify |> println

   11 + 9*sqrt(6)/2

y は通分ぐらいしか手がない。

res[1][3] |> factor |> println

   2*(39 + 16*sqrt(6))/15

   r1 = 6.0000000
   x = 22.0227038;  y = 10.4255781

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, x, y) = (6, 11 + 9*sqrt(6)/2, (78 + 32*sqrt(6))/15)
   @printf("r1 = %.7f\n", r1)
   @printf("x = %.7f;  y = %.7f\n", x, y)
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   circle(r3 + r1, 0, r1, :red)
   circle(-r3 - r1, 0, r1, :red)
   circle(0, r3 + r2, r2, :blue)
   circle(0, -r3 - r2, r2, :blue)
   circle(0, 0, r3, :green)
   if more == true
       point(r3, 0, " r3", :green)
       point(0, 0, "小円", :green, :center, :top, mark=false)
       point(r3 + r1, 0, " r3+r1", :red)
       point(r3 + r1, r3, "大円", :red, mark=false)
       point(x, 0, " x", :black)
       point(0, r3 + r2, "r3+r2", :blue, :right, :bottom)
       point(0, r3 + r2, " 中円", :blue, :left, :bottom, mark=false)
       point(0, y, "y ", :black, :right, :bottom)
       point(0, r3, "r3", :blue, :right, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その232）

算額（その232）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（222)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

団扇の中に大円 2 個、小円 １ 個がある。扇の径が 9 寸、大円の径が 4寸5分のとき、小円の径はいかほどか。

大円の半径と中心座標を r1, (x1, y1), r1 = r0//2, y1 = 0
小円の半径と中心座標を r2, (0, r0 - r2)
団扇面を切り欠く円の中心座標を (0, y), y < 0
団扇面の円と扇面を切り欠く円の交点座標を (x0, y0)
とし，連立方程式を解く。
なお，団扇面を切り欠く円の半径，中心については条件式が与えられていないので解は y を含む式になる。

include("julia-source.txt")

using SymPy
@syms r0::positive, r1::positive, y1,
     r2::pisitive, r::positive, y::negative,
     x0::positive, y0::negative;
r0 = 9 
r1 = r0 // 2
y1 = 0
y0 = -sqrt(r0^2 - x0^2)
eq1 = r1^2 + (r0 - r2 -y1)^2 - (r1 + r2)^2
eq3 = r1^2 + (y1 - y)^2 - (r + r1)^2
eq5 = sqrt(r^2 - x0^2) + y + sqrt(r0^2 - x0^2)
res = solve([eq1, eq3, eq5], (r2, r, x0))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))

たとえば y = -9 のとき，
r2 = 3
r  = 5.562305898749054
x0 = 5.2900672706322585
になる。

y = -9
(3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))

   (3, 5.562305898749054, 5.2900672706322585)

   小円半径 = 3.00000
   団扇面の円を切り欠く円の中心 = (0, -9.00000);  半径 = 5.56231
   2円の交点 = (5.29007, -7.28115)

using Printf
using Plots

function draw(y, more)
   pyplot(size=(500, 500), grid=false, aspect_ratio=1, label="", fontfamily="IPAMincho")
   r0 = 9 
   r1 = 9//2
   y1 = 0
   (r2, r, x0) = (3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))
   y0 = -sqrt(r0^2 - x0^2)
   @printf("小円半径 = %.5f\n", r2)
   @printf("団扇面の円を切り欠く円の中心 = (0, %.5f);  半径 = %.5f\n", y, r)
   @printf("2円の交点 = (%.5f, %.5f)\n", x0, y0)
   θ = Int(round(atand((y0 - y)/x0), digits=0))
   plot()
   circle(0, 0, r0, :black)
   circle(0, r0 - r2, r2)
   circle(r1, y1, r1, :blue)
   circle(-r1, y1, r1, :blue)
   circle(0, y, r, :black, beginangle=θ, endangle=180 - θ)
   for deg = 90:10:180-θ
       plot!([-r*cosd(deg), 0, r*cosd(deg)], [r*sind(deg) + y, -r0, r*sind(deg) + y], color=:black, lw=2)
   end
   if more
       point(0, r0, " r0", :black, :left, :bottom)
       point(0, r0 - r2, " r0-r2", :red, :left, :bottom)
       point(x0, y0, "(x0,y0)")
       point(r1, y1, " r1", :blue)
       point(r0, y1, " r0 ", :black, :right)
       point(0.2r1, (2r0 - r2)/2, "小円", :red, mark=false)
       point(r1, r1/2, "大円", :blue, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;