算額(その245)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3(228)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)
長方形内に大円 1 個,小円 2個が長方形に接して入っている。長方形の長辺と短辺はそれぞれ 15寸,8寸である。大円と片方の小円の共通接線(界斜)があるとき界斜の長さはいかほどか。
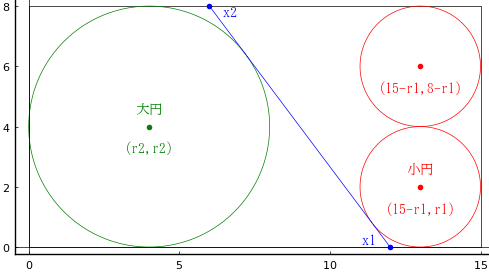
長方形の左下角を原点とする。
大円の半径,中心座標を r2, (r2, r2) とする。r2 = 4 である。
小円の半径,中心座標を r1, (15 - r1, r1), (15 - r1, 8 - r1) とする。r1 = 2 である。
界斜と長方形の下辺,上辺の交点座標を (x1, 0), (x2, 8) とする。
大円と下側の小円の中心から界斜までの距離に関する以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::positive, x1::positive, x2::positive;
r1 = 2
r2 = 4
eq1 = distance(x1, 0, x2, 8, 15 - r1, r1) - r1^2;
eq2 = distance(x1, 0, x2, 8, r2, r2) - r2^2;
res = solve([eq1, eq2], (x1, x2))
3-element Vector{Tuple{Sym, Sym}}:
(5, 20)
(12, 6)
(22, 44/9)
二番目の解が適切である。すなわち,界斜は座標 (12, 0), (6, 8) を結ぶ線分。
長さは sqrt((12 - 6)^2 + (8 - 0)^2) = 10 寸である。
sqrt((12 - 6)^2 + (8 - 0)^2)
10.0
using Plots
using Printf
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x1, x2) = res[2]
@printf("x1 = %.2f; x2 = %.2f; 界斜の長さ = %.2f\n", x1, x2, sqrt((x2 - x1)^2 + 8^2))
plot([0, 15, 15, 0, 0], [0, 0, 8, 8, 0], color=:black, lw=0.5)
circle(15 - r1, r1, r1)
circle(15 - r1, 8 - r1, r1)
circle(r2, r2, r2, :green)
segment(x1, 0, x2, 8, :blue)
if more == true
point(15 - r1, 1.2r1, "小円", :red, :center, :bottom, mark=false)
point(15 - r1, r1, "\n(15-r1,r1)", :red, :center, :top)
point(15 - r1, 8 - r1, "\n(15-r1,8-r1)", :red, :center, :top)
point(r2, 1.1r2, "大円", :green, :center, :bottom, mark=false)
point(r2, r2, "\n(r2,r2)", :green, :center, :top)
point(x1, 0, "x1 ", :blue, :right, :bottom)
point(x2, 8, " x2", :blue, :left, :top)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;