算額(その241)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3(227)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)
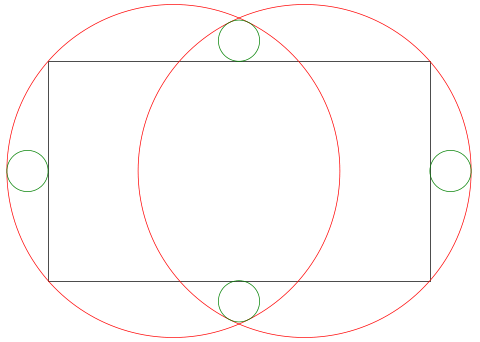
2 個の大円が交わり,その中に長方形と小円が 4 個入っている。小円の径を知って,大円の径を求めよ。

大円に接する長方形の右上の頂点座標を (x, y) とおく。
大円,小円の半径と中心座標を以下のようにおく。
大円: r1, (x1, 0) ただし与えられた条件より r1 = 1 とする。
小円: r2, (0, y + r2) および (x + r2, 0)

以下の連立方程式を立てるが,問では条件が一つ足りない。そこで,x と y の間に x = ny のような制約条件を追加して解く(以下では x = 2y とした)。
なお,nlsolve() ではこの制約条件を追加しなくても一応の解は得られる。
include("julia-source.txt");
using SymPy
@syms x::positive, y::positive, r1::positive, x1::positive, r2::positive;
r2 = 1
x = 2y
eq1 = (x - x1)^2 + y^2 - r1^2 |> expand
eq2 = x - x1 + 2r2 - r1 |> expand
eq3 = x1^2 + (y + r2)^2 - (r1 - r2)^2 |> expand
eq4 = ((2r1 - 2r2)^2 + y^2) + (4r2^2 + y^2) - (2r1)^2 |> expand;
res = solve([eq1, eq2, eq3], (x1, r1, y))
1-element Vector{Tuple{Sym, Sym, Sym}}:
(-5*sqrt(2)*(8*sqrt(2) + 71)^(2/3)/289 + sqrt(2)*(8*sqrt(2) + 71)^(1/3)/34 + 21/16 + 99*(8*sqrt(2) + 71)^(1/3)/272 + 421*(8*sqrt(2) + 71)^(2/3)/4624, -3*sqrt(2)*(8*sqrt(2) + 71)^(2/3)/289 - sqrt(2)*(8*sqrt(2) + 71)^(1/3)/34 + 173*(8*sqrt(2) + 71)^(1/3)/272 + 715*(8*sqrt(2) + 71)^(2/3)/4624 + 59/16, 3/2 + 17/(4*(sqrt(2) + 71/8)^(1/3)) + (sqrt(2) + 71/8)^(1/3))
x1 = 4.33657; r1 = 8.92148; y = 5.62902; x = 11.25805
小円の半径を 1 としたので,8.92148 は大円の半径である。

using Printf
function draw(x1, r1, x, y, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r2 = 1
@printf("x1 = %.5f; r1 = %.5f; y = %.5f; x = %.5f\n", x1, r1, y, x)
plot([x, x, -x, -x, x], [-y, y, y, -y, -y], color=:black, lw=0.5)
circle(x1, 0, r1)
circle(-x1, 0, r1)
circle(0, y + r2, r2, :green)
circle(0, -y - r2, r2, :green)
circle(x + r2, 0, r2, :green)
circle(-x - r2, 0, r2, :green)
if more == true
point(x1, 0, "x1 ", :red, :right)
point(x + r2, 0, "x+r2 ", :green, :right)
point(0, y + r2, " y+r2", :green, :left, :bottom)
point(x + 2r2, 0, " x+2r2", :red)
point(x, y, " (x,y)", :red, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
(x1, r1, y) = res[1]
---
条件不足のまま 4元連立方程式を nlsolve() で x1, r1, x, y について解く。
using SymPy
@syms x::positive, y::positive, r1::positive, x1::positive, r2::positive;
r2 = 1
eq1 = (x - x1)^2 + y^2 - r1^2 |> expand
eq2 = x - x1 + 2r2 - r1 |> expand
eq3 = x1^2 + (y + r2)^2 - (r1 - r2)^2 |> expand
eq4 = ((2r1 - 2r2)^2 + y^2) + (4r2^2 + y^2) - (2r1)^2 |> expand;
println(eq1, ", # eq1")
println(eq2, ", # eq2")
println(eq3, ", # eq3")
println(eq4, ", # eq4")
-r1^2 + x^2 - 2*x*x1 + x1^2 + y^2, # eq1
-r1 + x - x1 + 2, # eq2
-r1^2 + 2*r1 + x1^2 + y^2 + 2*y, # eq3
-8*r1 + 2*y^2 + 8, # eq4
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
v = r.zero
end
return v, r.f_converged
end;
function H(u)
r1 = 1
(x1, r1, x, y) = u
return [
-r1^2 + x^2 - 2*x*x1 + x1^2 + y^2, # eq1
-r1 + x - x1 + 2, # eq2
-r1^2 + 2*r1 + x1^2 + y^2 + 2*y, # eq3
-8*r1 + 2*y^2 + 8, # eq4
]
end;
iniv = [big"4.0", 9, 10, 6]
res2 = nls(H, ini=iniv);
println((res2));
(BigFloat[3.183012652585522591832434702426538376856770104448615704443237602882606475256619, 8.076648273506633325075325119429150245928992397056981109398659352229911092241916, 9.259660926092155916907759821855688622785762501505596813841896955962457886997144, 5.320394073189178089410508073953356392935683449161830208448592642794610637849292], true)
x1 = 3.18301; r1 = 8.07665; y = 5.32039; x = 9.25966