算額（その254）

算額（その254）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額4（199)
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

角錐台に大球と小球が外接して入っている。小球は上面，大球は下面に接し，それぞれは4つの側面にも外接している。上面，下面の正方形の一辺がそれぞれ 125寸，2000寸のとき，小球の直径を求めよ。

側面方向からの透視図を描くと，図に示すように等脚台形の中に大小の円が入っていることになる。

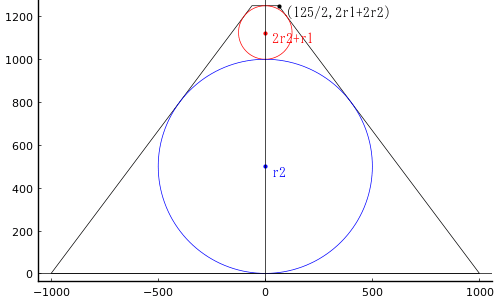
大円の半径と中心座標を r2, (0, r2)
小円の半径と中心座標を r1, (0, 2r2 + r1)
それぞれの円の中心から台形の脚への距離について，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, a::positive, b::positive;

a = 125//2
b = 2000//2
eq1 = distance(a, 2r2+2r1, b, 0, 0, 2r2 + r1) - r1^2
eq2 = distance(a, 2r2+2r1, b, 0, 0, r2) - r2^2
res = solve([eq1, eq2], (r1, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (125, 500)

小球の直径は 2 × 125 = 250寸，大球の直径は 2 × 500 = 1000寸

a, b を変数のまま連立方程式を解くと，r1, r2 は a, b を含む式になる。

using SymPy

@syms r1::positive, r2::positive, a::positive, b::positive;

# a = 125//2
# b = 2000//2
eq1 = distance(a, 2r2+2r1, b, 0, 0, 2r2 + r1) - r1^2
eq2 = distance(a, 2r2+2r1, b, 0, 0, r2) - r2^2
res = solve([eq1, eq2], (r1, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (a^(3/4)*b^(1/4), a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2))

r1 = a^(3/4)*b^(1/4)
r2 = a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2)
それぞれを求める関数を以下のようにする。

f_r1(a, b) = a^(3/4)*b^(1/4);
f_r2(a, b) = a^(7/4)*b^(3/4)*(-sqrt(a) + sqrt(b))/(a^(3/2)*sqrt(b) - a^2);

f_r1(big"125"/2, big"2000"/2)*2

   250.0

f_r2(big"125"/2, big"2000"/2)*2

   1000.0

なお，術では，小球の直径 = sqrt(a * sqrt(a * b)) であるがこれは，上述の a^(3/4) * b^(1/4) に等しい。

@syms a::positive, b::positive;
sqrt(a * sqrt(a * b))|> simplify |> println

   a^(3/4)*b^(1/4)

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (125, 500)
   plot([1000, 125/2, -125/2, -1000, 1000], [0, 2r1 + 2r2, 2r1 + 2r2, 0, 0], linecolor=:black, linewidth=0.5)
   circle(0, 2r2 + r1, r1)
   circle(0, r2, r2, :blue)
   if more == true
       point(0, r2, " r2", :blue)
       point(0, 2r2 + r1, " 2r2+r1", :red)
       point(125/2, 2r1 + 2r2, " (125/2,2r1+2r2)", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;

算額（その253）

算額（その253）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額4（199)
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

鉤股弦において，鉤と股の積が 52440 平方寸，股と弦の積が 130065 平方寸のとき，鉤，股，弦それぞれの長さを求めよ。

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms 鉤::positive, 股::positive, 弦::positive;

eq1 = 鉤 * 股 - 52440
eq2 = 股 * 弦 - 130065
eq3 = 鉤^2 + 股^2 - 弦^2
res = solve([eq1, eq2, eq3], (鉤, 股, 弦))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (152, 345, 377)

鉤 = 152, 股 = 345, 弦 = 377 である。

using Plots
using Printf

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鉤, 股, 弦) = (152, 345, 377)
   plot([0, 股, 0, 0], [0, 0, 鉤, 0], linecolor=:black, linewidth=0.5)
   if more == true
       point(0, 鉤/2, " 鉤 = 152寸", :green, :left, :bottom, mark=false)
       point(股/2, 0, " 股 = 345寸", :blue, :center, :bottom, mark=false)
       point(股/2, 鉤/2, " 弦 = 377寸", :red, :left, :bottom, mark=false)
   else
      plot!(showaxis=false)
   end
end;