算額(その603)
和算図形問題あれこれ
令和4年11月の問題-No.2 額題輯録より
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html
外円の中に 9 個の円が互いに接して入っている。東円,南円,土円の直径がそれぞれ 198 寸,66 寸,36 寸のとき,外円,火円の直径を求めよ。
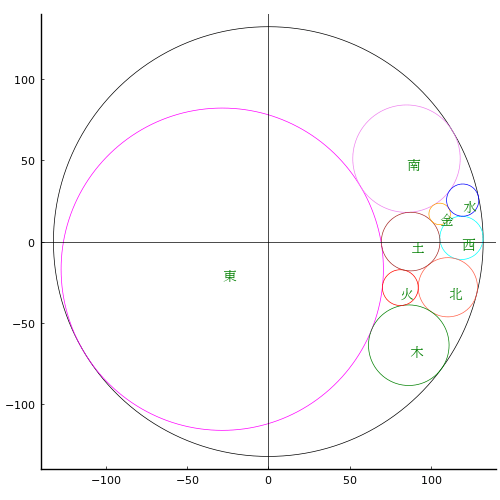
以下のようにおき,連立方程式を解く。
外円の半径と中心座標を R, (0, 0)
東円の半径と中心座標を r1, (x1, y1); r1 = 198/2
西円の半径と中心座標を r2, (x2, y2)
南円の半径と中心座標を r3, (x3, y3); r3 = 66/2
北円の半径と中心座標を r4, (x4, y4)
木円の半径と中心座標を r5, (x5, y5)
火円の半径と中心座標を r6, (x6, y6)
土円の半径と中心座標を r7, (x7, y7); r7 = 36/2, y7 = 0
金円の半径と中心座標を r8, (x8, y8)
水円の半径と中心座標を r9, (x9, y9)
include("julia-source.txt");
using SymPy
@syms r1, x1, y1, r2, x2, y2, r3, x3, y3, r4, x4, y4, r5, x5, y5,
r6, x6, y6, r7, x7, y7, r8, x8, y8, r9, x9, y9, R
y7 = 0
(r1, r3, r7) = (198, 66, 36) .// 2
eq01 = (x1 - x5)^2 + (y1 - y5)^2 - (r1 + r5)^2
eq02 = (x1 - x6)^2 + (y1 - y6)^2 - (r1 + r6)^2
eq03 = (x1 - x7)^2 + (y1 - y7)^2 - (r1 + r7)^2
eq04 = (x1 - x3)^2 + (y1 - y3)^2 - (r1 + r3)^2
eq05 = x1^2 + y1^2 - (R - r1)^2
eq06 = (x2 - x4)^2 + (y2 - y4)^2 - (r2 + r4)^2
eq07 = (x2 - x7)^2 + (y2 - y7)^2 - (r2 + r7)^2
eq08 = (x2 - x8)^2 + (y2 - y8)^2 - (r2 + r8)^2
eq09 = (x2 - x9)^2 + (y2 - y9)^2 - (r2 + r9)^2
eq10 = x2^2 + y2^2 - (R - r2)^2
eq11 = (x3 - x7)^2 + (y3 - y7)^2 - (r3 + r7)^2
eq12 = (x3 - x8)^2 + (y3 - y8)^2 - (r3 + r8)^2
eq13 = (x3 - x9)^2 + (y3 - y9)^2 - (r3 + r9)^2
eq14 = x3^2 + y3^2 - (R - r3)^2
eq15 = (x4 - x5)^2 + (y4 - y5)^2 - (r4 + r5)^2
eq16 = (x4 - x6)^2 + (y4 - y6)^2 - (r4 + r6)^2
eq17 = (x4 - x7)^2 + (y4 - y7)^2 - (r4 + r7)^2
eq18 = x4^2 + y4^2 - (R - r4)^2
eq19 = (x5 - x6)^2 + (y5 - y6)^2 - (r5 + r6)^2
eq20 = x5^2 + y5^2 - (R - r5)^2
eq21 = (x6 - x7)^2 + (y6 - y7)^2 - (r6 + r7)^2
eq22 = (x7 - x8)^2 + (y7 - y8)^2 - (r7 + r8)^2
eq23 = (x8 - x9)^2 + (y8 - y9)^2 - (r8 + r9)^2
eq24 = x9^2 + y9^2 - (R - r9)^2;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(x1, y1, r2, x2, y2, x3, y3, r4, x4, y4, r5, x5, y5,
r6, x6, y6, x7, r8, x8, y8, r9, x9, y9, R) = u
return [
-(r5 + 99)^2 + (x1 - x5)^2 + (y1 - y5)^2, # eq01
-(r6 + 99)^2 + (x1 - x6)^2 + (y1 - y6)^2, # eq02
y1^2 + (x1 - x7)^2 - 13689, # eq03
(x1 - x3)^2 + (y1 - y3)^2 - 17424, # eq04
x1^2 + y1^2 - (R - 99)^2, # eq05
-(r2 + r4)^2 + (x2 - x4)^2 + (y2 - y4)^2, # eq06
y2^2 - (r2 + 18)^2 + (x2 - x7)^2, # eq07
-(r2 + r8)^2 + (x2 - x8)^2 + (y2 - y8)^2, # eq08
-(r2 + r9)^2 + (x2 - x9)^2 + (y2 - y9)^2, # eq09
x2^2 + y2^2 - (R - r2)^2, # eq10
y3^2 + (x3 - x7)^2 - 2601, # eq11
-(r8 + 33)^2 + (x3 - x8)^2 + (y3 - y8)^2, # eq12
-(r9 + 33)^2 + (x3 - x9)^2 + (y3 - y9)^2, # eq13
x3^2 + y3^2 - (R - 33)^2, # eq14
-(r4 + r5)^2 + (x4 - x5)^2 + (y4 - y5)^2, # eq15
-(r4 + r6)^2 + (x4 - x6)^2 + (y4 - y6)^2, # eq16
y4^2 - (r4 + 18)^2 + (x4 - x7)^2, # eq17
x4^2 + y4^2 - (R - r4)^2, # eq18
-(r5 + r6)^2 + (x5 - x6)^2 + (y5 - y6)^2, # eq19
x5^2 + y5^2 - (R - r5)^2, # eq20
y6^2 - (r6 + 18)^2 + (x6 - x7)^2, # eq21
y8^2 - (r8 + 18)^2 + (x7 - x8)^2, # eq22
-(r8 + r9)^2 + (x8 - x9)^2 + (y8 - y9)^2, # eq23
x9^2 + y9^2 - (R - r9)^2, # eq24
]
end;
iniv = BigFloat[-47.596, 62.827, 36.173, 144.692, -22.846, 102.808, 83.769, 55.212, 85.673, -95.192, 68.538, -39.981, -108.519, 24.75, 24.75, -38.077, 74.25, 15.231, 121.846, 20.942, 24.75, 156.115, 34.269, 182.769]
res = nls(H, ini=iniv)
外円の直径 = 264; 火円の直径 = 22
東円: r1 = 99; x1 = -28.2973; y1 = -16.9784
西円: r2 = 13.2985; x2 = 118.68; y2 = 2.28068
南円: r3 = 33; x3 = 84.8918; y3 = 50.9351
北円: r4 = 18.1837; x4 = 110.302; y4 = -28.0663
木円: r5 = 24.75; x5 = 86.3067; y5 = -63.6688
火円: r6 = 11; x6 = 81.1188; y6 = -28.2973
土円: r7 = 18; x7 = 87.4643; y7 = 0
金円: r8 = 6.6; x8 = 105.266; y8 = 16.9784
水円: r9 = 9.9; x9 = 119.414; y9 = 25.4675
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
y7 = 0
(r1, r3, r7) = (198, 66, 36) .//2
(x1, y1, r2, x2, y2, x3, y3, r4, x4, y4, r5, x5, y5,
r6, x6, y6, x7, r8, x8, y8, r9, x9, y9, R) = res[1]
@printf("外円の直径 = %g; 火円の直径 = %g\n", 2R, 2r6)
@printf("東円: r1 = %g; x1 = %g; y1 = %g\n", r1, x1, y1)
@printf("西円: r2 = %g; x2 = %g; y2 = %g\n", r2, x2, y2)
@printf("南円: r3 = %g; x3 = %g; y3 = %g\n", r3, x3, y3)
@printf("北円: r4 = %g; x4 = %g; y4 = %g\n", r4, x4, y4)
@printf("木円: r5 = %g; x5 = %g; y5 = %g\n", r5, x5, y5)
@printf("火円: r6 = %g; x6 = %g; y6 = %g\n", r6, x6, y6)
@printf("土円: r7 = %g; x7 = %g; y7 = %g\n", r7, x7, y7)
@printf("金円: r8 = %g; x8 = %g; y8 = %g\n", r8, x8, y8)
@printf("水円: r9 = %g; x9 = %g; y9 = %g\n", r9, x9, y9)
plot()
circle(0, 0, R, :black)
circle(x1, y1, r1, :magenta)
circle(x2, y2, r2, :cyan)
circle(x3, y3, r3, :violet)
circle(x4, y4, r4, :tomato)
circle(x5, y5, r5, :green)
circle(x6, y6, r6, :red)
circle(x7, y7, r7, :brown)
circle(x8, y8, r8, :orange)
circle(x9, y9, r9, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(x1, y1, "東", mark=false)
point(x2, y2, "西", mark=false)
point(x3, y3, "南", mark=false)
point(x4, y4, "北", mark=false)
point(x5, y5, "木", mark=false)
point(x6, y6, "火", mark=false)
point(x7, y7, "土", mark=false)
point(x8, y8, "金", mark=false)
point(x9, y9, "水", mark=false)
end
end;