算額（その664）

算額（その664）

北海道函館市谷地頭町 函館八幡宮 文化2年(1805)
中村信弥「幻の算額」
http://www.wasan.jp/maborosi/maborosi.html

正方形の中に半円 2 個と容円 1 個が入っている容円の直径を「黒積」で表わせ。

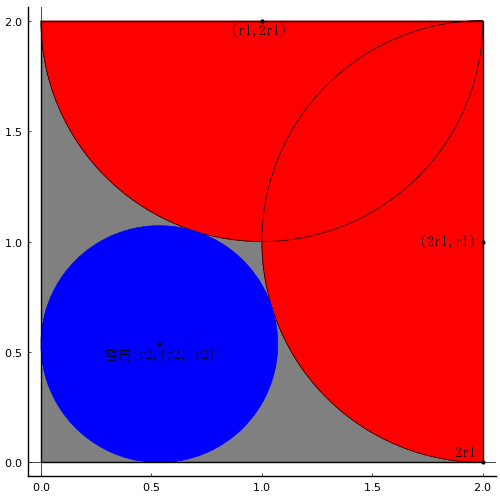
黒積とは，名前とは相反して「図形の背景の空白領域の面積」を表すことが常識的であるようだ。この問題の場合は，正方形の内部の半円，容円以外の部分，図で灰色で示した部分の面積を指す。

半円の半径と中心座標を r1, (2r1, r1)
容円の半径と中心座標を r2, (r2, r2)
黒積を A とする。
正方形の一辺の長さは 2r1 である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1::positive, r2::positive, A::positive
s3 = sqrt(Sym(3));

黒積 A は

(2r1)^2 -(PI*r1^2 - 2(PI*r1^2/4 - r1^2/2)) - PI*r2^2
= -PI*r1^2/2 + 3*r1^2 - PI*r2^2

である。

(2r1)^2 -(PI*r1^2 - 2(PI*r1^2/4 - r1^2/2)) - PI*r2^2 |> simplify |> println

   -pi*r1^2/2 + 3*r1^2 - pi*r2^2

eq1 = A - (-PI*r1^2/2 + 3*r1^2 - PI*r2^2)
eq1 |> println

   A - 3*r1^2 + pi*r1^2/2 + pi*r2^2

eq1 から solve() により r1 を求める。

res = solve(eq1, r1)[1]
res |> println  # r1

   sqrt(2*A + 2*pi*r2^2)/sqrt(6 - pi)

r1 を表すこの式には r2 が含まれるので，r2 を消去する。

そこで，半円と容円が外接することに基づき，半円，容円の半径の関係を求める。
最初の解が適解である。すなわち，r2 = 2(2 - √3)*r1 である。

eq2 = (2r1 - r2)^2 + (r1 - r2)^2 - (r1 + r2)^2
res = solve(eq2, r2)
res |> println

   Sym[2*r1*(2 - sqrt(3)), 2*r1*(sqrt(3) + 2)]

この r1 に上で求めた式を代入し，方程式 eq2 を解いて r2 を求めれば，A を含む式で解が得られる。

eq2 = 2*(sqrt(2*A + 2*PI*r2^2)/sqrt(6 - PI))*(2 - s3) - r2 |> simplify
eq2 |> println

   (-r2*sqrt(6 - pi) + (4 - 2*sqrt(3))*sqrt(2*A + 2*pi*r2^2))/sqrt(6 - pi)

res = solve(eq2, r2)[1] |> sympy.sqrtdenest |> simplify;

res |> display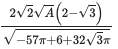



res |> println

   2*sqrt(2)*sqrt(A)*(2 - sqrt(3))/sqrt(-57*pi + 6 + 32*sqrt(3)*pi)

容円の半径は
2*sqrt(2)*sqrt(A)*(2 - sqrt(3))/sqrt(-57*pi + 6 + 32*sqrt(3)*pi)
である。

この式が正しいことを逆算して確かめる。
黒積 A が 2 のとき，容円の半径 r2 は 1.0440008465400472 である。

r2 = (2*sqrt(2)*sqrt(2)*(2 - sqrt(3))/sqrt(-57*pi + 6 + 32*sqrt(3)*pi))

   1.0440008465400472

r2 = 2*r1*(2 - sqrt(3)) なので，半円の半径 r1 は 1.9481321012161867 である。

r1 = r2/(2(2 - sqrt(3)))

   1.9481321012161867

黒積は，以下の通り 1.9999999999999942 ≒ 2 になる。

-pi*r1^2/2 + 3*r1^2 - pi*r2^2

   1.9999999999999942

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1
   r2 = 2*r1*(2 - sqrt(3))
   @printf("r1 = %g;  r2 = %g\n", r1, r2)
   plot([0, 2r1, 2r1, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5,seriestype=:shape, fillcolor=:gray)
   circlef(2r1, r1, r1, beginangle=90, endangle=270)
   circlef(r1, 2r1, r1, beginangle=180, endangle=360)
   circle(2r1, r1, r1, :black, beginangle=90, endangle=270)
   circle(r1, 2r1, r1, :black, beginangle=180, endangle=360)
   circlef(r2, r2, r2, :blue)
   plot!([0, 2r1, 2r1, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(2r1, 0, "2r1 ", :black, :right, :bottom, delta=delta/2)
       point(2r1, r1, "(2r1,r1) ", :black, :right, :vcenter)
       point(r1, 2r1, "(r1,2r1) ", :black, :center, delta=-delta/2)
       point(r2, r2, "容円:r2,(r2, r2)", :black, :center, delta=-delta/2)
   end
end;

算額（その663）

算額（その663）

茨城県真壁郡十里村 子権現 文化10年(1813)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

直角三角形内に中鈎，大円，中円，小円を入れる。中円，小円の直径が 1寸6分，1寸2分のとき，大円の中心と底辺の右側の頂点を結ぶ斜線（線分）の長さを求めよ。

直角を挟む二辺のうち，短い方を「鈎」，長い方を「股」，斜辺を「弦」とする。直角の頂点から弦への垂線を「中鈎」，垂線の脚の座標を (x, y) とする。
大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (x2, r2)
小円の半径と中心座標を r3, (r3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     長弦::positive, 短弦::positive, 中鈎::positive,
     r1::positive, r2::positive, r3::positive,
     x2::positive, y3::positive,
     x::positive, y::positive
eq1 = x^2 + y^2 - 中鈎^2
eq2 = 鈎^2 - 中鈎^2 - 短弦^2
eq3 = 股^2 - 中鈎^2 - 長弦^2
eq4 = 鈎^2 + 股^2 - 弦^2
eq5 = r1/(股 - r1) - r2/(股 - x2)
eq6 = 鈎 + 股 - 弦 - 2r1
eq7 = 中鈎 + 長弦 - 股 - 2r2
eq8 = 短弦 + 中鈎 - 鈎 - 2r3
eq9 = y/(股 - x) - 鈎/股
eq10 = distance(0, 鈎, 股, 0, r3, y3) - r3^2
eq11 = distance(0, 0, x, y, r3, y3) - r3^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (鈎, 股, 弦, 長弦, 短弦, 中鈎, r1, x2, y3, x, y) = u
   return [
x^2 + y^2 - 中鈎^2,  # eq1
-中鈎^2 - 短弦^2 + 鈎^2,  # eq2
-中鈎^2 + 股^2 - 長弦^2,  # eq3
-弦^2 + 股^2 + 鈎^2,  # eq4
r1/(-r1 + 股) - r2/(-x2 + 股),  # eq5
-2*r1 - 弦 + 股 + 鈎,  # eq6
-2*r2 + 中鈎 - 股 + 長弦,  # eq7
-2*r3 + 中鈎 + 短弦 - 鈎,  # eq8
y/(-x + 股) - 鈎/股,  # eq9
-r3^2 + (r3 - 股*(r3*股 - y3*鈎 + 鈎^2)/(股^2 + 鈎^2))^2 + (y3 - 鈎*(-r3*股 + y3*鈎 + 股^2)/(股^2 + 鈎^2))^2,  # eq10
-r3^2 + (r3 - x*(r3*x + y*y3)/(x^2 + y^2))^2 + (-y*(r3*x + y*y3)/(x^2 + y^2) + y3)^2,  # eq11
   ]
end;

(r2, r3) = (16, 12) .// 20
iniv = BigFloat[3.12, 4.21, 4.9, 3.54, 1.57, 2.34, 0.97, 1.57, 1.71, 1.31, 1.97]
res = nls(H, ini=iniv)

   (BigFloat[2.999999999999999999999999999999999999999999999998364504764585263757442728869067, 3.99999999999999999999999999999999999999999999999983729201826455417895867769145, 4.999999999999999999999999999999999999999999999998887822096160394442079955076626, 3.200000000000000000000000000000000000000000000001750994840687508520418164311052, 1.800000000000000000000000000000000000000000000000278207587008218098902215488639, 2.399999999999999999999999999999999999999999999998086297177577045658540513381006, 0.9999999999999999999999999999999999999999999999996569873433447117471607257418246, 1.599999999999999999999999999999999999999999999998962056077717036894336519529871, 1.799999999999999999999999999999999999999999999998692438333645772214535803150353, 1.440000000000000000000000000000000000000000000000475520887507759448903957591724, 1.919999999999999999999999999999999999999999999998011029938669057719045586200767], true)

鈎 = 3;  股 = 4;  弦 = 5;  長弦 = 3.2;  短弦 = 1.8;  中鈎 = 2.4;  r1 = 1;  x2 = 1.6;  y3 = 1.8;  x = 1.44;  y = 1.92

「斜線」は (r1, r1) と (股, 0) を結ぶものなので，その長さは sqrt((股 - r1)^2 +(r1 - 0)^2) = sqrt(10) = 3.1622776601683795 である。

sqrt(10)

   3.1622776601683795

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3) = (16, 12) .// 20
   (鈎, 股, 弦, 長弦, 短弦, 中鈎, r1, x2, y3, x, y) = res[1]
   @printf("鈎 = %g;  股 = %g;  弦 = %g;  長弦 = %g;  短弦 = %g;  中鈎 = %g;  r1 = %g;  x2 = %g;  y3 = %g;  x = %g;  y = %g\n",
           鈎, 股, 弦, 長弦, 短弦, 中鈎, r1, x2, y3, x, y)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
   circle(r1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(r3, y3, r3, :orange)
   segment(0, 0, x, y)
   segment(r1, r1, 股, 0, :cyan, lw=1)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(r1, r1, " 大円:r1\n (r1,r1)", :red, :left, :bottom)
       point(x2, r2, "中円:r2\n(x2,r2)", :blue, :center, delta=-delta)
       point(r3, y3, "小円:r3\n(r3,y3)", :orange, :left, delta=-delta)
       point(2.5, 0.65, "斜線", :brown, mark=false)
       point(0, 鈎, " 鈎", :green, :left, :bottom)
       point(股, 0, " 股", :green, :left, :bottom, delta=delta/2)
       point(x, y, " (x,y)", :green, :left, :bottom)
       plot!(xlims=(-0.2, 4.2))
   end
end;