算額（その657）

算額（その657）

千葉胤秀『算法新書』，文政13年(1830)
一関博物館>>和算に挑戦>>平成17年度出題問題(1)[中級問題]&解答例
https://www.city.ichinoseki.iwate.jp/museum/wasan/h17/normal.html

平成17年度中級
大，中，小の正方形が図のように配置されている。左右の大正方形は同じ大きさである。小サイズの正方形の一辺の長さが 1cm のとき，中サイズの正方形の一辺の長さはいかほどか。

中サイズの正方形の右端の頂点の座標を (x1, √2 + x1) とする。また，大正方形が x 軸と接する座標を (x2, 0) とすると，x2 = √2/2 + (√2 + x1 - √2/2) である。
以下の方程式を解いて x1 を得る。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms x1::positive

x2 = sqrt(Sym(2))/2 + (sqrt(Sym(2)) + x1 - sqrt(Sym(2))/2)
eq = (x1 - sqrt(Sym(2))/2)^2 + (sqrt(Sym(2)) + x1 - sqrt(Sym(2))/2)^2 - (x2 - sqrt(Sym(2))/2)^2 - (sqrt(Sym(2))/2)^2
solve(eq)[1] |> println # x1

   sqrt(2)

x1 = √2 なので，中正方形の一辺の長さは sqrt(2x1^2) = 2 である。
中正方形の一辺の長さは 2cm である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   x1 = √2
   x2 = √2/2 + (√2 + x1 - √2/2)
   plot([0, √2/2, 0, -√2/2, 0], [0, √2/2, √2, √2/2, 0], color=:blue, lw=0.5)
   plot!([0, x1, 0, -x1, 0], [√2, √2 + x1, √2 + 2x1, √2 + √2, √2])
   plot!([√2/2, x2, x2 + x1 - √2/2, x1, √2/2], [√2/2, 0, √2 + x1 - √2/2, √2 + x1, √2/2])
   plot!(-[√2/2, x2, x2 + x1 - √2/2, x1, √2/2], [√2/2, 0, √2 + x1 - √2/2, √2 + x1, √2/2])
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(√2/2, √2/2, " (√2/2,√2/2)", :black, :left, :bottom, delta=delta/3)
       point(x2, 0, " x2", :black, :left, :bottom, delta=delta/3)
       point(x1, √2 + x1, " (x1,√2+x1)", :black, :left, :bottom, delta=delta/3)
       point(0, √2, " √2", :black, :left, :vcenter)
       point(0, √2 + 2x1, " √2+2x1", :black, :left, :vcenter)
       point(2, 1.7, "大", mark=false)
       point(0.3, 3, "中", mark=false)
       point(0.1, 0.8, "小", mark=false)
   end
end;

算額（その656）

算額（その656）

百十一 高崎市倉賀野町 倉賀野神社 慶応3年(1867)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.

群馬の和算 111(1/2) 倉賀野神社
http://takasakiwasan.web.fc2.com/gunnsann/g111_1.html

キーワード：累円，円弧，正三角形
#Julia, #SymPy, #算額, #和算，#数学

正三角形内に最も大きな円弧を置き，その円弧と2辺に接する甲円を置く。甲円と円弧と底辺に接する乙円を置き，同様に順次丙円，丁円...を置く。
これらの直径を求めよ。

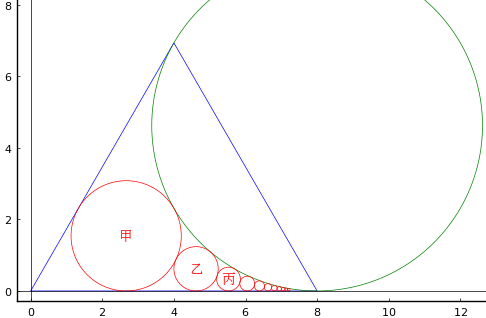
正三角形の一辺の長さを a とおき，甲円，乙円...の半径と中心座標を (r1, x1), (r2, x2)...とする。

甲円のパラメータ (r1, x1) が決まったあと，乙円のパラメータは (r1, x1) で記述できる。その後も，丙円，丁円と同じ関係式でパラメータが決まる。

まず最初に，正三角形内の最大弧を決定する。弧を形成する円は正三角形の 2 つの辺に頂点で接するものである。その中心座標は (a, a/√3) であることは簡単な計算で分る。この中心座標を (x, y) とおき，甲円の r1, x1 を以下の連立方程式を解いて求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, a::positive,
     r1::positive, x1::positive,
     r2::positive, x2::positive
a = 8
R = a/sqrt(Sym(3))
(x, y) = (a, R)
eq1 = (x - x1)^2 + (y - r1)^2 - (R + r1)^2
eq2 = r1/x1 - y/x
res = solve([eq1, eq2], (r1, x1))

   2-element Vector{Tuple{Sym, Sym}}:
    (8*sqrt(3)/9, 8/3)
    (8*sqrt(3), 24)

2 組の解が得られるが，2 番目のものが適解である。
すなわち，r1 = 8*sqrt(3)/9, x1 = 8/3 である。

次に，乙円のパラメータ r2, x2 は，r1, x1 を未知数のままにして（r2, x2 が r1, x1 を含む式で表される）以下の連立方程式で求めることができる。

eq3 = (x - x2)^2 + (y - r2)^2 - (R + r2)^2
eq4 = (x2 - x1)^2 + (r1 - r2)^2 - (r1 + r2)^2;

簡単な二元連立方程式であるが，SymPy の能力的に solve([eq3, eq4], (r2, x2)) は有限の時間内には解けないようなので，手動で解く。

まず，eq4 から x2 を求める。x2 は r2 が決まれば求めることができる。

# x2 を求める式
solve(eq4, x2) |> println

   Sym[-2*sqrt(r1)*sqrt(r2) + x1, 2*sqrt(r1)*sqrt(r2) + x1]

2 組の解が得られるが，2 番目のものが適解である。 すなわち，x2 = 2*sqrt(r1)*sqrt(r2) + x1 である。この式は算額において有名な式で，つまる所は，直線の上に載っている，互いに接している円の中心間の水平距離は 2 つの円の積の平方根の 2 倍である，つまり，x2 - x1 = 2√(r1*r2) にほかならない。

得られた x2 を eq3 に代入すると以下の方程式が得られる。

eq3 = (x - (2sqrt(r1)*sqrt(r2) + x1))^2 + (y - r2)^2 - (R + r2)^2
eq3 |> println

   (-r2 + 8*sqrt(3)/3)^2 - (r2 + 8*sqrt(3)/3)^2 + (-2*sqrt(r1)*sqrt(r2) - x1 + 8)^2

この方程式から r2 を求める。

res = solve(eq3, r2)
res |> println

   Sym[(x1 - 8)^2*(4*sqrt(2)*3^(3/4)*sqrt(r1)*(-3*r1^2 + 16*sqrt(3)*r1 - 64) + (3*r1 + 8*sqrt(3))*(3*r1^2 - 16*sqrt(3)*r1 + 64))/(4*(3*r1^2 - 16*sqrt(3)*r1 + 64)^2), (x1 - 8)^2*(4*sqrt(2)*3^(3/4)*sqrt(r1) + 3*r1 + 8*sqrt(3))/(4*(3*r1^2 - 16*sqrt(3)*r1 + 64))]

2 組の解が得られるが，最初のものが適解である。 簡約化すると以下のようになる。

# r2 を求める式
r2 = res[1] |> simplify |> println

   (x1 - 8)^2*(-4*sqrt(2)*3^(3/4)*sqrt(r1) + 3*r1 + 8*sqrt(3))/(4*(3*r1^2 - 16*sqrt(3)*r1 + 64))

以上で求めた r2, x2 を求める式は r1, x1 だけを含む。また，この式は互いに接する円の間に成り立つので，たとえば丙円と丁円の間においても成り立つ。そこで，以下のような関数としてまとめておく。

function nextcircle(r1, x1)
   # # r2 = (x1 - 8)^2*(-4*sqrt(Sym(2))*3^Sym(3//4)*sqrt(r1) + 3*r1 + 8*sqrt(Sym(3)))/(4*(3*r1^2 - 16*sqrt(Sym(3))*r1 + 64))
   r2 = (x1 - 8)^2*(-4*sqrt(2)*3^(3/4)*sqrt(r1) + 3*r1 + 8*sqrt(3))/(4*(3*r1^2 - 16*sqrt(3)*r1 + 64))
   x2 = 2*sqrt(r1)*sqrt(r2) + x1
   return (r2, x2)
end;

この関数を使って，累円のパラメータを求めてみよう。

(r1, x1) = (8*sqrt(3)/9, 8/3)

   (1.5396007178390019, 2.6666666666666665)

nextcircle(1.5396007178390019, 2.6666666666666665)

   (0.6188021535170058, 4.618802153517006)

nextcircle(0.6188021535170058, 4.618802153517006)

   (0.3316150746190428, 5.524791385931975)

nextcircle(0.3316150746190428, 5.524791385931975)

   (0.20626738450566878, 6.04786451314966)

   甲円の直径 = 3.0792014;  中心の X 座標 = 2.6666667
   乙円の直径 = 1.2376043;  中心の X 座標 = 4.6188022
   丙円の直径 = 0.6632301;  中心の X 座標 = 5.5247914
   丁円の直径 = 0.4125348;  中心の X 座標 = 6.0478645
   戊円の直径 = 0.2811508;  中心の X 座標 = 6.3884294
   己円の直径 = 0.2038283;  中心の X 座標 = 6.6278172
   庚円の直径 = 0.1545148;  中心の X 座標 = 6.8052841
   辛円の直径 = 0.1211510;  中心の X 座標 = 6.9421037
   壬円の直径 = 0.0975328;  中心の X 座標 = 7.0508060
   癸円の直径 = 0.0802036;  中心の X 座標 = 7.1392508

術では以下のような解が述べられている。関係式は簡潔であるが，直径（半径）の情報しか得られない。上述した式は半径と中心座標を求めることができる解である。

極 = 8/sqrt(0.75)
甲 = 極/3; 甲 |> println
子 = 甲*極; 乙 = 子/(2√子 + 極 + 甲); 乙 |> println
丑 = 乙*極; 丙 = 丑/(2√丑 + 極 + 乙); 丙 |> println

   3.0792014356780046
   1.2376043070340124
   0.6632301492380859

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   n = length(names)
   rs = Vector{Float64}(undef, n)
   xs = Vector{Float64}(undef, n)
   a = 8
   R = a/sqrt(Sym(3))
   (x, y) = (a, R)
   plot([0, a, a/2, 0], [0, 0, √3a/2, 0], color=:blue, lw=0.5)
   circle(x, y, R, :green)
   (r1, x1) = (8*sqrt(3)/9, 8/3)
   circle(x1, r1, r1)
   for i = 1:n
       @printf("%s円の直径 = %.7f;  中心の X 座標 = %.7f\n", names[i], 2r1, x1)
       (rs[i], xs[i]) = (r1, x1)
       (r2, x2) = nextcircle(r1, x1)
       circle(x2, r2, r2)
       (r1, x1) = (r2, x2)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       for i = 1:3
           point(xs[i], rs[i], names[i], :red, :center, :vcenter, mark=false)
       end
   end
end;