算額(その648)
岐阜県不破郡垂井町宮代 南宮大社奉納算額 天保13年
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
楕円の中に大,中,小の正方形を入れる。大正方形の一辺の長さが与えられたとき,小正方形の一辺の長さを求めよ。
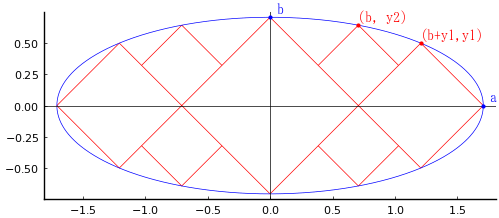
楕円の長径,短径を a, b
大正方形の一辺の長さを '大'
小正方形の一辺の長さを '小'
中正方形の楕円の周上の座標を (b + y1, y1)
小正方形の楕円の周上の座標を (b, y2)
とおき,以下の連立方程式を解く。
eq5 は'大'を求めてから単純に計算するだけであるが,面倒くさいので入れておく。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms 大::positive, 小::positive, a::positive, b::positive, y1::positive, y2::positive
eq1 = b + 2y1 - a
eq2 = b^2/a^2 + y2^2/b^2 - 1
eq3 = (b + y1)^2/a^2 + y1^2/b^2 - 1
eq4 = b - 大/sqrt(Sym(2))
eq5 = y2/sqrt(Sym(2)) - 小;
res = solve([eq1, eq2, eq3, eq4, eq5], (小, a, b, y1, y2))
1-element Vector{NTuple{5, Sym}}:
(大*sqrt(-2 + 2*sqrt(2))/2, 大*(sqrt(2) + 2)/2, sqrt(2)*大/2, 大/2, 大*sqrt(-1 + sqrt(2)))
小正方形の一辺の長さは,大正方形の一辺の長さの √(2√2 - 2)/2 倍である。
大正方形の一辺の長さを 1 とすると,小正方形の一辺の長さは 0.455089860562227 である。
その他のパラメータは以下の通り。
a = 1.70711; b = 0.707107; y1 = 0.5; y2 = 0.643594
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
大 = 1
(小, a, b, y1, y2) = (大*sqrt(-2 + 2*sqrt(2))/2, 大*(sqrt(2) + 2)/2, sqrt(2)*大/2, 大/2, 大*sqrt(-1 + sqrt(2)))
@printf("小正方形の一辺の長さ = %g; a = %g; b = %g; y1 = %g; y2 = %g\n",
小, a, b, y1, y2)
plot([a, b + y1, 0, -b - y1, -a, -b - y1, 0, b + y1, a],
[0, y1, -b, y1, 0, -y1, b, -y1, 0], color=:red, lw=0.5)
x = [b - y2/2, b, b + y2/2]
y = [y2/2, y2, y2/2]
plot!(x, y, color=:red, lw=0.5)
plot!(x, -y, color=:red, lw=0.5)
plot!(-x, y, color=:red, lw=0.5)
plot!(-x, -y, color=:red, lw=0.5)
ellipse(0, 0, a, b, color=:blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(b, y2, "(b, y2)", :red, :left, :bottom, delta=delta/2)
point(b + y1, y1, "(b+y1,y1)", :red, :left, :bottom, delta=delta/2)
end
end;



















