算額（その647）

算額（その647）

長野県長和町 駒形神社 明治8年(1875)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

5 個の等円が隣の等円と外接し円弧に外接している。両端の等円は弦の延長線に接している。
矢が 8 寸，弦が 24 寸のとき，等円の直径を求めよ。

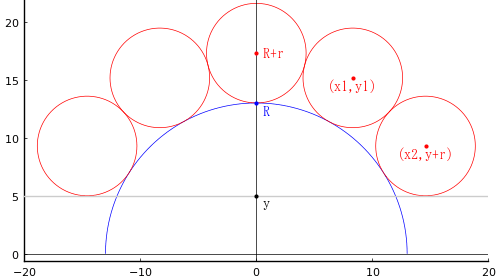
円弧が一部である円の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (0, R + r), (x1, y1), (x2, y + r)
弦と y 軸の交点座標を (0, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, r::positive, y::positive,
     x1::positive, y1::positive, x2::positive, y2::positive

eq1 = x1^2 + y1^2 - (R + r)^2
eq2 = x2^2 + (y + r)^2 - (R + r)^2
eq3 = x1^2 + (R + r - y1)^2 - 4r^2
eq4 = (x2 - x1)^2 + (y1 - y - r)^2 - 4r^2
eq5 = y - sqrt(R^2 - 12^2)
eq6 = y - (R - 8)

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (R, r, y, x1, y1, x2) = u
   return [
       x1^2 + y1^2 - (R + r)^2,  # eq1
       x2^2 - (R + r)^2 + (r + y)^2,  # eq2
       -4*r^2 + x1^2 + (R + r - y1)^2,  # eq3
       -4*r^2 + (-x1 + x2)^2 + (-r - y + y1)^2,  # eq4
       y - sqrt(R^2 - 144),  # eq5
       -R + y + 8,  # eq6
   ]
end;
g = 12
iniv = BigFloat[13, 4.3, 5, 8.3, 15, 14.6]
res = nls(H, ini=iniv)

   (BigFloat[13.0, 4.292842863236655796258424878247800048144346796834551378448796255304952228172366, 5.0, 8.316932815223808406463820238890995876085407092697237813856266028198192952429316, 15.16149870031483123032399683773288234968648696208586379659490076589161640834934, 14.58374046024498108560260206110599459102827635604655955326101083845210751031903], true)

等円の直径は約 8.58569 となるが，中村も指摘しているように，題意が不明瞭であることと，原問題の条件と答えに合う図にならない。

その他のパラメータは以下の通り。
R = 13;  r = 4.29284; y = 5;  x1 = 8.31693;  y1 = 15.1615;  x2 = 14.5837

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r, y, x1, y1, x2) = res[1]
   @printf("等円の直径 = %g;  R = %g;  r = %g; y = %g;  x1 = %g;  y1 = %g;  x2 = %g\n",
       2r, R, r, y, x1, y1, x2)
   plot()
   circle(0, 0, R, :blue, beginangle=0, endangle=180)
   circle(0, R + r, r, :red)
   circle(x1, y1, r, :red)
   circle(-x1, y1, r, :red)
   circle(x2, y + r, r, :red)
   circle(-x2, y + r, r, :red)
   hline!([y], color=:gray80)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, y, " y", :black, :left, delta=-delta/2)
       point(0, R, " R", :blue, :left, delta=-delta/2)
       point(0, R + r, " R+r", :red, :left, :vcenter)
       point(x1, y1, "(x1,y1)", :red, :center, delta=-delta/2)
       point(x2, y + r, "(x2,y+r)", :red, :center, delta=-delta/2)
   end
end;

算額（その646）

算額（その646）

長野県東御市 大日如来堂（長命寺） 嘉永6年(1853)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

二等辺三角形に初円は底辺と斜辺に接している。順次，第n円は (n - 1) 円と斜辺に接している。
二等辺三角形の高さを h，底辺の長さを 2a，斜辺の長さを b とする。

初円の半径と中心座標を r1, (0, r1)
二円の半径と中心座標を r2, (0, 2r1 + r2)
とおき，以下の連立方程式を解き r1, r2 を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, h::positive, r1::positive, r2::positive, b1::positive, b2::positive

h = sqrt(b^2 - a^2)
sinθ = a/sqrt(a^2 + h^2)
eq1 = r1/(h - r1) - sinθ
eq2 = r2/(h - 2r1 - r2) - sinθ;
res = solve([eq1, eq2], (r1, r2))

   Dict{Any, Any} with 2 entries:
     r2 => a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2)
     r1 => a*sqrt(-a^2 + b^2)/(a + b)

r1 = a*sqrt(-a^2 + b^2)/(a + b)
r2 = a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2);

これらの円は互いに相似なので，半径は初項が r1，公比が r2/r1 の等比数列になる。
n 番目の円（最終の円）の半径は以下の式で表される。

@syms n
eq11 = r1*(r2/r1)^(n - 1) |> simplify
eq11 |> println

   a*(a + b)*(-a^2 + b^2)^(n - 1/2)/(a^2 + 2*a*b + b^2)^n

この半径が最大になるときの底辺の長さは，eq11 を a で偏微分し，導関数が　0 になるときの a を求めればよい。

eq12 = diff(eq11, a) |> simplify
eq12 |> println

   (-a^2 + b^2)^(n - 1/2)*(a^2 + 2*a*b*n - a*b - b^2)/((a - b)*(a^2 + 2*a*b + b^2)^n)

SymPy は「この式 = 0」をそのまま解くことができない。

式の項を検討すると，a^2 + 2*a*b*n - a*b - b^2 = 0 を解けばよいことがわかる。
式を直接書いてもよいが，args で取り出す。

eq12.args

   (1/(a - b), (-a^2 + b^2)^(n - 1/2), (a^2 + 2*a*b + b^2)^(-n), a^2 + 2*a*b*n - a*b - b^2)

eq12.args[4] |> println

   a^2 + 2*a*b*n - a*b - b^2

res = solve(eq12.args[4], a)
res |> println

   Sym[b*(-2*n - sqrt(4*n^2 - 4*n + 5) + 1)/2, b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1)/2]

2 番目のものが適解である。

底辺の長さは b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1) である。

2res[2] |> println

   b*(-2*n + sqrt(4*n^2 - 4*n + 5) + 1)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (n, b) = (4, 15)
   println("n = $n;  b = $b")
   a = b*(sqrt(4n^2 - 4n + 5) - 2n + 1)
   println("a = $a")
   h = sqrt(b^2 - a^2)
   println("h = $h")
   r1 = a*sqrt(-a^2 + b^2)/(a + b)
   r2 = a*(-a + b)*sqrt(-a^2 + b^2)/(a^2 + 2*a*b + b^2)
   plot([a, 0, -a, a], [0, h, 0, 0], color=:gray80, lw=0.5)
   circle(0, r1, r1, :blue)
   circle(0, 2r1 + r2, r2, :red)
   r = zeros(n)
   r[1] = r1
   r[2] = r2
   y = zeros(n)
   for i = 3:n
       r[i] = r1*(r2/r1)^(i - 1)
       y[i] = 2sum(r[1:i]) - r[i]
       circle(0, y[i], r[i], i)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, r1, " (0,r1)", :blue, :left, :vcenter)
       point(0, 2r1 + r2, " (0,2r1+r2)", :red, :left, :vcenter)
       point(0, y[3], " (0,2r1+2r2+r3)", :green, :left, :vcenter)
       point(0, y[4], " (0,2r1+2r2+2r3+r4)", :purple, :left, :vcenter)
   end
end;