算額（その655）

算額（その655）

『蠡管算法　巻上』の第１３問 をまなぶ（１／１）
http://takasakiwasan.web.fc2.com/kaihouhenomiti_1/reikannsannpou_jyou_13.html

「算法直術正解」第35問
http://takasakiwasan.web.fc2.com/kaihouhenomiti_1/pdf/sanpochokujutuseikai_35_2.pdf

団扇の中に菱形と 2 つの等円が入っている。団扇の直径が 10 寸で，菱形の一辺の長さが 6 寸の場合，等円の直径はいかほどか。

後者では 14 ページにわたる解法を示している。

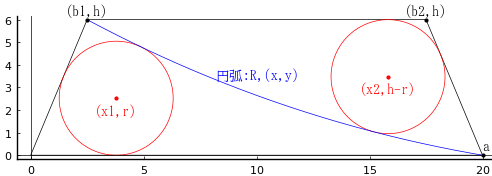
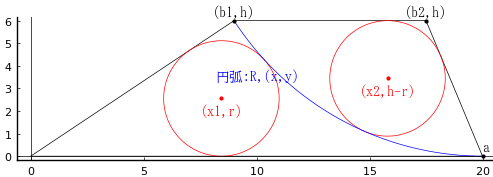
菱形の長径と短径を 2a, 2b
団扇の半径と中心座標を R, (0, 0)
等円の半径と中心座標を r, (x, y)
とする。

菱形の一辺の長さが 6 寸で，右端の頂点が半径 5 の円周上にあることから以下の方程式の eq4 を立てるが，R が与えられているので，b = 18/5 であることが容易に計算できる。

eq1 は等円が団扇に内接すること，eq2 は扇の下部の弧と等円が外接すること，eq3 は等円の中心と菱形の右下の辺までの距離が等円の直径であることを表している。この 3 方程式を解くと r, x, y が正確に求まる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R::positive, a::positive, b::positive,
     r::positive, x::positive, y::negative
R = 10//2
b = 18//5
eq1 = x^2 + y^2 - (R - r)^2
eq2 = x^2 + (y + R)^2 - (2R - 2b + r)^2
eq3 = distance(0, R - 2b, sqrt(R^2 - (R - b)^2), R - b, x, y) - r^2
eq4 = sqrt(6^2 - b^2) - sqrt(R^2 - (R - b)^2);
res = solve([eq1, eq2, eq3], (r, x, y))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (26208/17405, 51408/17405, -6499/3481)

等円の直径は 2*26208/17405 = 3.011548405630566
中心座標は (2.9536340132145935, -1.8669922436081585) である。

2*26208/17405, 51408/17405, -6499/3481

   (3.011548405630566, 2.9536340132145935, -1.8669922436081585)

団扇の円と下部の円弧の交点座標 (ax, ay) は以下の連立方程式を解いて求めることができる。

@syms ax::positive, ay::negative
eq5 = ax^2 + ay^2 - R^2
eq6 = ax^2 + (ay + R)^2 - (2R - 2b)^2
solve([eq5, eq6], (ax, ay))

   1-element Vector{Tuple{Sym, Sym}}:
    (336/125, -527/125)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10//2
   b = 18//5
   (r, x, y) = res[1]
   a = sqrt(6^2 - b^2)
   @printf("等円の直径 = %g;  r = %g;  x = %g;  y = %g;  a = %g;   b = %g\n",
       2r, r, x, y, a, b)
   plot([a, 0, -a, 0, a], [R - b, R, R - b, R - 2b, R-b], color=:blue, lw=0.5)
   circle(0, 0, R)
   circle(x, y, r, :green)
   (ax, ay) = (336/125, -527/125)
   @printf("ax = %g; ay = %g\n", ax, ay)
   θ = atand((R + ay)/ax)
   println(θ)
   circle(0, -R, 2R - 2b, :orange, beginangle=θ, endangle=180-θ)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, R - b, " R-b")
       point(0, R - 2b, " R-2b")
       point(a, R - b, "(a,R-b) ", :blue, :right, :vcenter)
       point(x, y, "(x,y)")
       point(ax, ay, "(ax,ay)")
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その654）

算額（その654）

群馬の算額 44-2 八幡宮
http://takasakiwasan.web.fc2.com/gunnsann/g044-2.html

下底 20 寸，上底 15 寸，高さ 6 寸の台形内に，円弧と等円 2 個を置く。等円の直径を求めよ。

算額の原図を左右反転させ，台形の左下頂点を原点に置き，下底の長さを a，高さを h とする。
台形は等脚台形でなくてもよいので，左上，右上の頂点座標を(b1, h), (b2, h) とおく。
等円の半径と中心座標を r, (x1, r), (x2, h - r)
円弧を構成する円の半径と中心座標を R, (x, y)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b1::positive, b2::positive, h::positive,
     R::positive, x::positive, y::positive,
     r::positive, x1::positive, x2::positive
eq1 = (x - a)^2 + y^2 - R^2
eq2 = (x - b1)^2 + (y - h)^2 - R^2
eq3 = (x - x1)^2 + (y - r)^2 - (R + r)^2
eq4 = (x - x2)^2 + (y - h + r)^2 - (R - r)^2
eq5 = dist(0, 0, b1, h, x1, r) - r^2
eq6 = dist(a, 0, b2, h, x2, h - r) - r^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (R, x, y, r, x1, x2) = u
   return [
       -R^2 + y^2 + (-a + x)^2,  # eq1
       -R^2 + (-b1 + x)^2 + (-h + y)^2,  # eq2
       -(R + r)^2 + (-r + y)^2 + (x - x1)^2,  # eq3
       -(R - r)^2 + (x - x2)^2 + (-h + r + y)^2,  # eq4
       -r^2 + (-b1*(b1*x1 + h*r)/(b1^2 + h^2) + x1)^2 + (-h*(b1*x1 + h*r)/(b1^2 + h^2) + r)^2,  # eq5
       -r^2 + (-a + x2 - (-a + b2)*(h*(h - r) + (-a + b2)*(-a + x2))/(h^2 + (-a + b2)^2))^2 + (h - h*(h*(h - r) + (-a + b2)*(-a + x2))/(h^2 + (-a + b2)^2) - r)^2,  # eq6
   ]
end;

(a, b1, b2, h) = (20, 2.5, 17.5, 6)
iniv = BigFloat[58, 30, 57, 2.5, 4, 16]

res = nls(H, ini=iniv)

   (BigFloat[57.56982255166217430368373764600179694519317160797444036827676398212356912948373, 29.67870619946091644204851752021563342318059299182850454725481532377198840972876, 56.75039308176100628930817610062893081761006289283313826282654469433496619510539, 2.522911051212938005390835579514824797843665768189002299181505707691245681699234, 3.784366576819407008086253369272237196765498652305250418532069716249659729439736, 15.81805929919137466307277628032345013477088948787348219211610072959637679631966], true)

台形が等脚台形（h = 6;  a = 20;  b1 = 2.5;  b2 = 17.5）の場合，R = 57.5698;  x = 29.6787;  y = 56.7504;  r = 2.52291;  x1 = 3.78437;  x2 = 15.8181
となり，等円の直径は約 5.04582 である。

なお，台形は等脚台形でなくても構わない（条件の範囲内で）。
たとえば，下図のような場合，パラメータは以下の通りである。
h = 6;  a = 20;  b1 = 9;  b2 = 17.5;  R = 13.1643;  x = 20.0441;  y = 13.1643;  r = 2.55614;  x1 = 8.44236;  x2 = 15.7959

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, x, y, r, x1, x2) = res[1]
   @printf("h = %g;  a = %g;  b1 = %g;  b2 = %g;  R = %g;  x = %g;  y = %g;  r = %g;  x1 = %g;  x2 = %g\n", h, a, b1, b2, R, x, y, r, x1, x2)
   plot([0, a, b2, b1, 0], [0, 0, h, h, 0], color=:black, lw=0.5)
   circle(x1, r, r)
   circle(x2, h - r, r)
   θ1 = atand((y - h)/(x - b1))
   θ2 = atand(y/(x - a))
   circle(x, y, R, :blue, beginangle=180 + θ1, endangle=180 + θ2, by=0.05)  
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x1, r, "(x1,r)", :red, :center, delta=-3delta)
       point(x2, h - r, "(x2,h-r)", :red, :center, delta=-3delta)
       point(b1, h, "(b1,h)", :black, :center, :bottom, delta=delta)
       point(b2, h, "(b2,h)", :black, :center, :bottom, delta=delta)
       point(a, 0, " a", :black, :center, :bottom, delta=delta)
       point(a/2, h/2, "円弧:R,(x,y)", :blue, :center, :bottom, delta=3delta, mark=false)
   end
end;