算額（その1347）

算額（その1347）

岐阜県垂井町 西法寺 令和6年(2024)
http://www.wasan.jp/gifu/saihoji.html

キーワード：三角錐，内接球，外接球，半径，中心座標
#Julia, #SymPy, #算額, #和算

三辺の長さが 3, 4, 7 である直方体の中に四面体 DEFG がある。表面積，外接球の半径，内接球の半径はいかほどか。

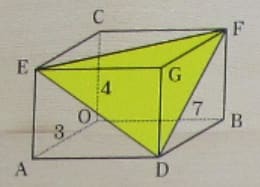
注：寸法の記述位置が若干曖昧であるが，OA = 3, OB = 7, OC = 4 である。

D, E, F, G の頂点座標を以下のように定義する。

x1, y1, z1 = 0, 0, 4  # E
x2, y2, z2 = 7, 0, 0  # D
x3, y3, z3 = 7, 3, 4  # G
x4, y4, z4 = 7, 0, 4;  # F

以下のプログラムにより，表面積，外接球の半径，内接球の半径を得る。

using LinearAlgebra

# 三角錐の体積を計算する関数
function tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
   M = [
       x1 y1 z1 1;
       x2 y2 z2 1;
       x3 y3 z3 1;
       x4 y4 z4 1
   ]
   return abs(det(M)) / 6
end

# 外接球の半径と中心を計算する関数
function circumsphere(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
   A = [
       x1 y1 z1 1;
       x2 y2 z2 1;
       x3 y3 z3 1;
       x4 y4 z4 1
   ]

   Dx = [
       x1^2 + y1^2 + z1^2 y1 z1 1;
       x2^2 + y2^2 + z2^2 y2 z2 1;
       x3^2 + y3^2 + z3^2 y3 z3 1;
       x4^2 + y4^2 + z4^2 y4 z4 1
   ]

   Dy = [
       x1^2 + y1^2 + z1^2 x1 z1 1;
       x2^2 + y2^2 + z2^2 x2 z2 1;
       x3^2 + y3^2 + z3^2 x3 z3 1;
       x4^2 + y4^2 + z4^2 x4 z4 1
   ]

   Dz = [
       x1^2 + y1^2 + z1^2 x1 y1 1;
       x2^2 + y2^2 + z2^2 x2 y2 1;
       x3^2 + y3^2 + z3^2 x3 y3 1;
       x4^2 + y4^2 + z4^2 x4 y4 1
   ]

   D = [
       x1^2 + y1^2 + z1^2 x1 y1 z1;
       x2^2 + y2^2 + z2^2 x2 y2 z2;
       x3^2 + y3^2 + z3^2 x3 y3 z3;
       x4^2 + y4^2 + z4^2 x4 y4 z4
   ]

   # 外接球の中心座標
   x_center = 0.5 * det(Dx) / det(A)
   y_center = -0.5 * det(Dy) / det(A)
   z_center = 0.5 * det(Dz) / det(A)

   # 外接球の半径
   radius = sqrt(x_center^2 + y_center^2 + z_center^2 - det(D) / det(A))

   return x_center, y_center, z_center, radius
end

# 内接球の半径と表面積を計算する関数
function insphere_radius(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
   # 各面の面積を求める
   area1 = 0.5 * norm(cross([x2 - x1, y2 - y1, z2 - z1], [x3 - x1, y3 - y1, z3 - z1]))
   area2 = 0.5 * norm(cross([x2 - x1, y2 - y1, z2 - z1], [x4 - x1, y4 - y1, z4 - z1]))
   area3 = 0.5 * norm(cross([x3 - x1, y3 - y1, z3 - z1], [x4 - x1, y4 - y1, z4 - z1]))
   area4 = 0.5 * norm(cross([x3 - x2, y3 - y2, z3 - z2], [x4 - x2, y4 - y2, z4 - z2]))

   # 表面積（4 面の合計）
   total_area = area1 + area2 + area3 + area4
   volume = tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)

   # 内接球の半径
   radius = 3 * volume / total_area

   return total_area, radius
end;

# 三角錐の体積
volume = tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("三角錐の体積: $volume")

# 外接球の中心と半径
x_center, y_center, z_center, circ_radius = circumsphere(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("外接球の中心: ($x_center, $y_center, $z_center)")
println("外接球の半径: $circ_radius")

# 内接球の半径と表面積
total_area, in_radius = insphere_radius(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("表面積: $total_area")
println("内接球の半径: $in_radius")

   三角錐の体積: 14.0
   外接球の中心: (3.499999999999999, 1.4999999999999996, 2.0)
   外接球の半径: 4.3011626335213125
   表面積: 49.0
   内接球の半径: 0.8571428571428571

「問」の条件に限定した検算

外心から各頂点までの距離

distance(a, b, c) = sqrt((a - 3.5)^2 + (b - 1.5)^2 + (c - 2)^2)
distance(x1, y1, z1) |>  println
distance(x2, y2, z2) |>  println
distance(x3, y3, z3) |>  println
distance(x4, y4, z4) |>  println

   4.301162633521313
   4.301162633521313
   4.301162633521313
   4.301162633521313

表面積

function h(a, b, c)
   s = (a + b + c)/2
   return sqrt(s*(s - a)*(s - b)*(s - c))
end
s1 = h(3, 4, 5)
s2 = h(3, 7, √58)
s3 = h(7, 4, √65)
s4 = h(√58, √65, 5)
S = s1 + s2 + s3 + s4

   49.0

体積

V = (3*4/2)*7/3

   14.0

内接円の半径

3V/S

   0.8571428571428571

四面体の表面積は 49，外接円の半径は 4.3011626335213125，内接円の半径は 0.8571428571428571 である。