算額(その1348)
岐阜県垂井町 西法寺 令和6年(2024)
http://www.wasan.jp/gifu/saihoji.html
キーワード:三角錐,内接球,外接球,半径,中心座標
#Julia, #SymPy, #算額, #和算
三辺の長さが 8, 9, 9 の四面体 OABC がある。体積,外接球の半径,内接球の半径はいかほどか。
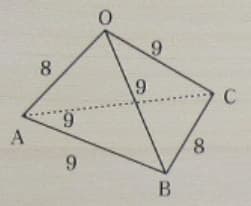

6 辺の長さが与えられているので,そのうちの一辺(AB)が x 軸上にあり,かつ片方の始点(A)が原点になるように座標を割り当て,頂点座標を求める。
その後は,算額(その214)に従って,解を得る。
include("julia-source.txt");
using SymPy
@syms x1, y1, x2, y2, z2
eq1 = x2^2 + y2^2 + z2^2 - 8^2
eq2 = (x2 - 9)^2 + y2^2 + z2^2 - 9^2
eq3 = (x2 - x1)^2 + (y2 - y1)^2 + z2^2 - 9^2
eq4 = x1^2 + y1^2 - 9^2
eq5 = (x1 - 9)^2 + y1^2 - 8^2
(x01, y01, x02, y02, z02) = solve([eq1, eq2, eq3, eq4, eq5], (x1, y1, x2, y2, z2))[4] # 4 of 4
(49/9, 8*sqrt(65)/9, 32/9, 128*sqrt(65)/585, 56*sqrt(65)/65)
x1, y1, z1 = 0, 0, 0
x2, y2, z2 = 9, 0, 0
x3, y3, z3 = x01.evalf(), y01.evalf(), 0
x4, y4, z4 = x02.evalf(), y02.evalf(), z02.evalf();
(x1, y1, z1) |> println
(x2, y2, z2) |> println
(x3, y3, z3) |> println
(x4, y4, z4) |> println
(0, 0, 0)
(9, 0, 0)
(5.44444444444444, 7.16645133182093, 0)
(3.55555555555556, 1.76404955860208, 6.94594513699567)
以下のプログラムにより,表面積,外接球の半径,内接球の半径を得る。
using LinearAlgebra
三角錐の体積を計算する関数
function tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
M = [
x1 y1 z1 1;
x2 y2 z2 1;
x3 y3 z3 1;
x4 y4 z4 1
]
return abs(det(M)) / 6
end
外接球の半径と中心を計算する関数
function circumsphere(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
A = [
x1 y1 z1 1;
x2 y2 z2 1;
x3 y3 z3 1;
x4 y4 z4 1
]
Dx = [
x1^2 + y1^2 + z1^2 y1 z1 1;
x2^2 + y2^2 + z2^2 y2 z2 1;
x3^2 + y3^2 + z3^2 y3 z3 1;
x4^2 + y4^2 + z4^2 y4 z4 1
]
Dy = [
x1^2 + y1^2 + z1^2 x1 z1 1;
x2^2 + y2^2 + z2^2 x2 z2 1;
x3^2 + y3^2 + z3^2 x3 z3 1;
x4^2 + y4^2 + z4^2 x4 z4 1
]
Dz = [
x1^2 + y1^2 + z1^2 x1 y1 1;
x2^2 + y2^2 + z2^2 x2 y2 1;
x3^2 + y3^2 + z3^2 x3 y3 1;
x4^2 + y4^2 + z4^2 x4 y4 1
]
D = [
x1^2 + y1^2 + z1^2 x1 y1 z1;
x2^2 + y2^2 + z2^2 x2 y2 z2;
x3^2 + y3^2 + z3^2 x3 y3 z3;
x4^2 + y4^2 + z4^2 x4 y4 z4
]
# 外接球の中心座標
x_center = 0.5 * det(Dx) / det(A)
y_center = -0.5 * det(Dy) / det(A)
z_center = 0.5 * det(Dz) / det(A)
# 外接球の半径
radius = sqrt(x_center^2 + y_center^2 + z_center^2 - det(D) / det(A))
return x_center, y_center, z_center, radius
end
内接球の半径と表面積を計算する関数
function insphere_radius(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
# 各面の面積を求める
area1 = 0.5 * norm(cross([x2 - x1, y2 - y1, z2 - z1], [x3 - x1, y3 - y1, z3 - z1]))
area2 = 0.5 * norm(cross([x2 - x1, y2 - y1, z2 - z1], [x4 - x1, y4 - y1, z4 - z1]))
area3 = 0.5 * norm(cross([x3 - x1, y3 - y1, z3 - z1], [x4 - x1, y4 - y1, z4 - z1]))
area4 = 0.5 * norm(cross([x3 - x2, y3 - y2, z3 - z2], [x4 - x2, y4 - y2, z4 - z2]))
# 表面積(4 面の合計)
total_area = area1 + area2 + area3 + area4
volume = tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
# 内接球の半径
radius = 3 * volume / total_area
return total_area, radius
end;
三角錐の体積
volume = tetrahedron_volume(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("三角錐の体積: $volume")
外接球の中心と半径
x_center, y_center, z_center, circ_radius = circumsphere(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("外接球の中心: ($x_center, $y_center, $z_center)")
println("外接球の半径: $circ_radius")
内接球の半径と表面積
total_area, in_radius = insphere_radius(x1, y1, z1, x2, y2, z2, x3, y3, z3, x4, y4, z4)
println("表面積: $total_area")
println("内接球の半径: $in_radius")
三角錐の体積: 74.6666666666667
外接球の中心: (4.50000000000000, 2.23262522260575, 1.73648628424892)
外接球の半径: 5.31507290636732
表面積: 128.996123972777
内接球の半径: 1.73648628424892
四面体の表面積は 74.6666666666667 = 224/3,外接円の半径は 5.31507290636732,内接円の半径は 1.73648628424892 である。