算額(その1517)
九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円10,外円,二等辺三角形
#Julia, #SymPy, #算額, #和算
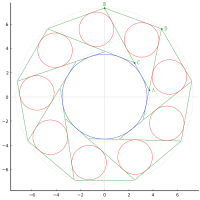
外円の中に二等辺三角形を容れ,甲円 4 個,乙円 2 個,丙円 4 個を容れる。丙円の直径が 1 寸のとき,甲円の直径はいかほどか。

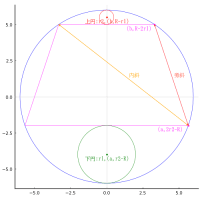
二等辺三角形の底辺と y 軸の交点座標を (0, y)
外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (r1, y - r1), (r1, y + r1)
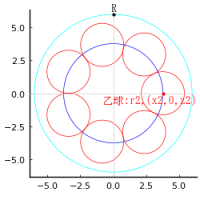
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3)
とおき,以下の連立方程式を解く。
include("julia-source.txt")
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r1, y, r2, x2, y2, r3, x3, y3
eq1 = r1^2 + (y - r1)^2 - (R - r1)^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq5 = y2/x2 * (y - R)/sqrt(R^2 - y^2) + 1
eq6 = dist(0, R, sqrt(R^2 - y^2), y, r1, y + r1) - r1^2
eq7 = dist(0, R, sqrt(R^2 - y^2), y, x2, y2) - r2^2
eq8 = dist(0, R, sqrt(R^2 - y^2), y, x3, y3) - r3^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (R, r1, y, r2, x2, y2, x3, y3))
eq1, eq2 の連立方程式を解いて r1, y を求める。式には R を含む。
res = solve([eq1, eq6], (r1, y))[3] # 3 of 3
(8*R/25, -7*R/25)
eq2, eq5, eq7 の r1, y に上で求められた式を代入して連立方程式を解き,r2,x2,y2 を求める。
eq12 = eq2(r1 => res[1], y => res[2]);
eq15 = eq5(r1 => res[1], y => res[2]);
eq17 = eq7(r1 => res[1], y => res[2]) |> simplify;
res2 = solve([eq12, eq15, eq17], (r2, x2, y2))[1] # 1 of 2
(R/5, 16*R/25, 12*R/25)
丙円の半径だけを求めるならば,算法助術の公式29 を用いる。y, r2 は上で求められた式を代入して方程式を解き,r3 を求める。
eq29 = (R^2 - y^2) + (R - y)^2 - 16r3*R
eq29_2 = eq29(y => res[2], r2 => res2[1])
ans_r3 = solve(eq29_2, r3)[1]
ans_r3 |> println
4*R/25
丙円の半径 r3 は,外円の半径 R の 4/25 倍である。
図を描くために x3, y3 も求めるならば,eq3, eq4, eq8 にそれまでに得られた r1, y, r2, x2, y2 を代入し,連立方程式を解いて r3, x3, y3 を求める。
eq13 = eq3(r1 => res[1], y => res[2])
eq14 = eq4(r1 => res[1], y => res[2], r2 => res2[1], x2 => res2[2], y2 => res2[3]) |> simplify
eq18 = eq8(r1 => res[1], y => res[2]) |> factor |> numerator
res3 = solve([eq13, eq14, eq18], (r3, x3, y3))[2]; # 3 of 3
# r3
res3[1] |> println
4*R/25
# x3
res3[2] |> println
4*R*(3*sqrt(5) + 19)/125
# y3
res3[3] |> println
R*(57/125 - 16*sqrt(5)/125)
以上で全てのパラメータは R を含む式で表された。
R 以外のパラメータを基準にするには,基準にするパラメータで割ればよい。
r3 を基準にして,r1 を求めるには以下のようにする。
# (R, r1, y, r2, x2, y2, r3, x3, y3)
(R, 8*R/25, -7*R/25, R/5, 16*R/25, 12*R/25, 4*R/25, 4*R*(3*sqrt(Sym(5)) + 19)/125, R*(57/125 - 16*sqrt(Sym(5))/125)) .// res3[1]
(25/4, 2, -7/4, 5/4, 4, 3, 1, 3*sqrt(5)/5 + 19/5, 2.85 - 4*sqrt(5)/5)
r3 = 4*R/25
r1 = 8*R/25
r1/r3 |> println
2
甲円の半径 r1 は,丙円の半径 r3 の 2 倍である。
丙円の直径が 1 寸のとき,甲円の直径は 2 寸である。
function draw(r3, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r1, y, r2, x2, y2, r3, x3, y3) = (25/4, 2, -7/4, 5/4, 4, 3, 1, 3*sqrt(5)/5 + 19/5, 2.85 - 4*sqrt(5)/5) ./ r3
plot([0, -sqrt(R^2 - y^2), sqrt(R^2 - y^2), 0], [R, y, y, R], color=:orange, lw=0.5)
circle(0, 0, R, :green)
circle2(r1, y + r1, r1)
circle2(r1, y - r1, r1)
circle2(x2, y2, r2, :magenta)
circle2(x3, y3, r3, :blue)
θ3 = atand(y3, x3)
θ2 = atand(y2, x2)
θ4 = θ2 + (θ2 - θ3)
circle2(sqrt(x3^2 + y3^2)*cosd(θ4), sqrt(x3^2 + y3^2)*sind(θ4), r3, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r1, y - r1, "甲円:r1,(r1,y-r1)", :red, :center, delta=-delta/2)
point(r1, y + r1, "甲円:r1,(r1,y+r1)", :red, :center, delta=-delta/2)
point(x2, y2, "乙円:r2\n(x2,y2)", :magenta, :center, delta=-delta/2)
point(x3, y3, "丙円:r3\n(x3,y3)", :blue, :center, delta=-delta/2)
point(0, R, "R", :green, :center, :bottom, delta=delta/2)
point(0, y, "y", :orange, :center, :bottom, delta=delta/2)
end
end;
draw(1/2, true)