ドット絵の丸が２つ

ドット絵の丸が２つ

締め切りが 2018/01/26 10:00 AM なので，その 1 分後に投稿されるように予約

【概要】
マス目に沿った、円のような形を２つ指定します。
両者に含まれるマスの数を計算してください。

【入出力】
入力は
1,2,3 4,5,4
のようになっています。
空白区切りで2つの図形が並んでいます。

各図形は、コンマ区切りで 中心のx座標、中心のy座標、半径 をならべたものです。
マス目の中心と中心の距離が、半径以下のマスが図形に含まれます。

具体的には下のとおりです：

上 0,0,0
中 1,2,3
下 4,5,6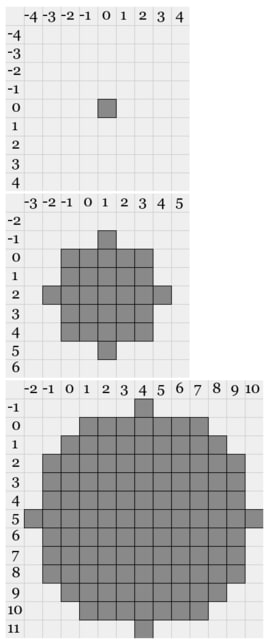


出力は、普通に10進数です。
2つの図形の両方に含まれるマスの数を答えてください。

【例】
上　入力 1,2,3 4,5,4　出力 10
中　0,1,5 4,8,6 出力 16
下　0,1,6 3,2,3　出力 28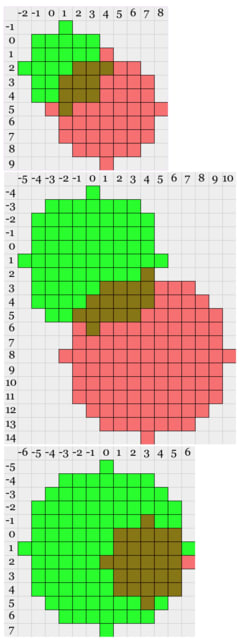


【補足】
    •    不正な入力に対処する必要はありません。
    •    中心座標は 0以上一万以下です。
    •    半径の値は 0以上一万以下です。
    •    中心座標・半径は、いずれも0以上の整数ですが、マス目はマイナスの座標にもあります。

==================================================

R だと，ベクトル演算とかその他のこそくな手段を用いても，制限時間の 1 秒を超える場合がある。

f = function(x1, y1, r1, x2, y2, r2) {
    r12 = r1^2
    r22 = r2^2
    count = 0
    for (x in (x1 - r1):(x1 + r1)) {
        x.x1 = r12-(x - x1)^2
        x.x2 = r22-(x - x2)^2
        if (x.x1 >= 0 && x.x2 >= 0) {
            temp = floor(sqrt(x.x1))
            count = count+sum(x.x2 >= ((y1 - temp):(y1 + temp) - y2)^2)
        }
    }
    cat(count)
}

#arg = as.integer(unlist(strsplit(readLines(file("stdin", "r"), "[, ]"))))
#f(arg[1], arg[2], arg[3], arg[4], arg[5], arg[6])

f(1, 2, 3, 4, 5, 4) # 10
f(0, 1, 5, 4, 8, 6) # 16
f(0, 1, 6, 3, 2, 3) # 28
f(0,0,0, 0,0,0) # 1
f(0,1,1, 0,2,1) # 2
f(1,1,1, 6,6,6) # 0
f(1,1,3, 7,7,7) # 5
f(7,14,17, 2,2,1) # 5
f(9,7,13, 8,4,18) # 529
f(12,15,17, 7,16,12) # 440
f(8,4,7, 16,16,7) # 0
system.time(f(2915,2254,4079, 9917,3046,7286)) # 24893077, 0.591sec.
system.time(f(5520,1032,740, 1982,2459,2672)) # 0, 0.091sec.
system.time(f(10000,10000,10000, 10000,10000,10000)) # 314159053, 5.600sec.
system.time(f(0,0,10000, 10000,10000,10000)) # 57079527, 2.815sec.

＝＝＝＝＝

Java では，あまり懲りすぎると帰って遅くなるので，以下の程度の最適化で十分。

    static int sq(int x) {
        return x * x;
    }

    static void f(int x1, int y1, int r1, int x2, int y2, int r2) {
        int minX, minY, maxX, maxY, count, x, y, r12, r22;
        minX = x1-r1;
        minY = y1 - r1;
        maxX = x1 + r1;
        maxY = y1 + r1;
        r12 = r1 * r1;
        r22 = r2 * r2;
        count = 0;
        for (x = minX; x
            if (sq(x-x1) > r12 || sq(x - x2) > r22) continue;
            for (y = minY; y
                if (r12 >= sq(x - x1) + sq(y - y1) && r22 >= sq(x - x2) + sq(y - y2)) {
                    count++;
                }
            }
        }
        System.out.println(count);
    }