算額(その609)
高山忠直編: 算法評論
国立国会図書館 デジタルコレクション
https://dl.ndl.go.jp/pid/3508431/1/10
直角三角形内に,甲円,乙円,丙円,丁円を入れる。甲円と乙円の直径がわかっているとき丙円の直径を求めよ。

直角三角形の直角を挟む二辺を鈎,股とする(鈎 < 股)
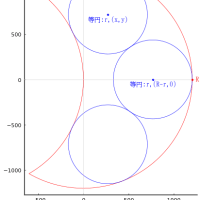
甲円の半径と中心座標を r1, (r1, r1)
乙円の半径と中心座標を r2, (y2, y2)
丙円の半径と中心座標を r3, (r3, y3)
丁円の半径と中心座標を r4, (r4, y4)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms 鈎::positive, 股::positive, r1::positive, y1, r2::negative, y2::positive, r3::positive, y3::negative, r4::positive, y4::positive
(x2, x3, x4) = (y2, y3, y4)
eq1 = (x2 - r1)^2 + (y2 - r1)^2 - (r1 + r2)^2
eq2 = (r1 - r4)^2 + (y4 - r1)^2 - (r1 + r4)^2
eq3 = (x2 - r3)^2 + (y3 - y2)^2 - (r2 + r3)^2
eq4 = (x2 - r4)^2 + (y2 - y4)^2 - (r2 + r4)^2
eq5 = (r3 - r4)^2 + (y3 - y4)^2 - (r3 + r4)^2
eq6 = distance(股, 0, 0, 鈎, r3, y3) - r3^2
eq7 = distance(股, 0, 0, 鈎, x2, y2) - r2^2;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(鈎, 股, y2, r3, y3, r4, y4) = u
return [
2*(-r1 + y2)^2 - (r1 + r2)^2, # eq1
(-r1 + y4)^2 + (r1 - r4)^2 - (r1 + r4)^2, # eq2
-(r2 + r3)^2 + (-r3 + y2)^2 + (-y2 + y3)^2, # eq3
-(r2 + r4)^2 + (-r4 + y2)^2 + (y2 - y4)^2, # eq4
(r3 - r4)^2 - (r3 + r4)^2 + (y3 - y4)^2, # eq5
-r3^2 + (r3 - 股*(r3*股 - y3*鈎 + 鈎^2)/(股^2 + 鈎^2))^2 + (y3 - 鈎*(-r3*股 + y3*鈎 + 股^2)/(股^2 + 鈎^2))^2, # eq6
-r2^2 + (y2 - 股*(y2*股 - y2*鈎 + 鈎^2)/(股^2 + 鈎^2))^2 + (y2 - 鈎*(-y2*股 + y2*鈎 + 股^2)/(股^2 + 鈎^2))^2, # eq7
]
end;
(r1, r2) = (9, 12)
iniv = BigFloat[75.6, 62.1, 25.6, 11.3, 44.0, 6.8, 26.5]
res = nls(H, ini=iniv)
(BigFloat[54.28853657836170682638366694115126793584060670779405752143209928308113720353747, 80.96484995197442957569524070254618022769191543098055398929484432041730484231544, 23.84924240491749801241773160420182982498155469145795476835513724890269102385213, 8.705582264797570515028006208872174856682679273246349361204917648446301735851336, 37.96981939330018192322196742329539101348115699766049412475605009936624145822072, 5.925450840795221324838051774317623074624056457781674516833436921472992954425592, 23.60534937167296822394913519268628446794816052457474295677168184443295330276947], true)
鈎 = 54.2885; 股 = 80.9648; r1 = 9; r2 = 12; y2 = 23.8492; r3 = 8.70558; y3 = 37.9698; r4 = 5.92545; y4 = 23.6053
甲円と乙円の直径が 18 寸,24 寸のとき丙円の直径は 17.4112 寸である。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鈎, 股, y2, r3, y3, r4, y4) = res[1]
(x2, x3, x4) = (y2, y3, y4)
@printf("丙円の直径 = %g\n", 2r3)
@printf("鈎 = %g; 股 = %g; r1 = %g; r2 = %g; y2 = %g; r3 = %g; y3 = %g; r4 = %g; y4 = %g\n",
鈎, 股, r1, r2, y2, r3, y3, r4, y4)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:brown, lw=0.5)
circle(r1, r1, r1)
circle(x2, y2, r2, :blue)
circle(r3, y3, r3, :green)
circle(x3, r3, r3, :green)
circle(r4, y4, r4, :magenta)
circle(x4, r4, r4, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(r1, r1, "甲円:r1\n(r1,r1)", :red, :center, delta=-delta)
point(y2, y2, "乙円:r2\n(y2,y2)", :blue, :center, delta=-delta)
point(r3, y3, "丙円:r3\n(r3,y3)", :green, :center, delta=-delta)
point(r4, y4, "丁円:r4\n(r4,y4)", :magenta, :center, :vcenter)
point(股, 0, "股", :brown, :left, :bottom, delta=delta)
point(0, 鈎, " 鈎", :brown, :left, :bottom)
end
end;



























※コメント投稿者のブログIDはブログ作成者のみに通知されます